Last updated: May 03, 2024

Bullet Energy Calculator

Q: How does barrel length affect muzzle velocity?

If everything else remains the same, a longer barrel length will allow the propellant gas to act on the bullet longer, thus accelerating it to higher speeds before exiting the muzzle. However, the propellant gas will start to lose pressure as it expands. So if the barrel is too long , the gas pressure cannot propel the bullet any further, and the friction between the bullet and the chamber will start to reduce its speed! Read more

Table of contents

Why is a bullet's energy important?Formula to calculate bullet energy How to calculate bullet energy in ft-lbs Example calculation of bullet kinetic energy Calculating muzzle energy and terminal energy Using this bullet energy calculator FAQs

Our bullet energy calculator will help you calculate the kinetic energy of a bullet. A bullet's destructive power comes from its kinetic energy due to its high velocity. Many bullets have muzzle velocities faster than the speed of sound (1130 ft/s or 343 m/s). Our calculator will help you understand how much energy a fast bullet might carry.

Don't miss the following article if you're interested in learning why a bullet's kinetic energy is essential and how to calculate bullet energy in ft-lbs. Let's start with what is a bullet.

Why is a bullet's energy important?

A bullet is a type of kinetic projectile, meaning its destructive power comes from its kinetic energy instead of explosives or other kinds of payload. When we say bullet energy, we're referring to the bullet's kinetic energy.

The kinetic energy is directly proportional to the bullet's mass and the square of its velocity. This allows bullets of small mass to possess high kinetic energies as long as they have high speeds, granting them incredible destructive and penetrating power.

🔎 For a deeper dive into kinetic energy, visit our kinetic energy calculator.

Understanding bullet energy is crucial for the following:

A bullet's kinetic energy is transferred to the target on impact. Thus, it is essential to determine the bullet's terminal ballistics, the bullet's performance once it impacts its target.
Conversely, high bullet energy also translates to high firearm recoil. The bullet energy will help ascertain the best firing stance to balance the recoil safely.
We can use the bullet's kinetic energy to compare different cartridges and pick the right one.

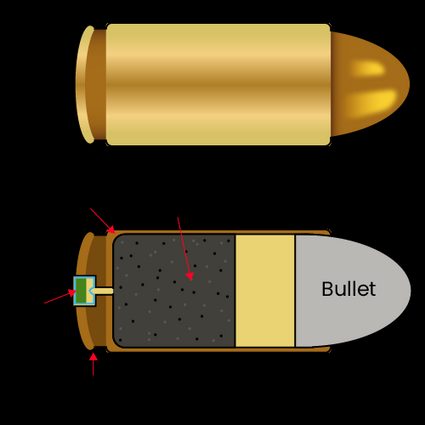
Cross section of a cartridge showing the bullet, propellant, case, rim, and primer. — Modern firearm ammunition comes in the form of *cartridges* or *rounds*. They are a pre-assembled package of a bullet (projectile), a propellant, and a primer for ignition.

As shown in the picture, the actual projectile is much smaller than the cartridge that contains it. Bullet mass is typically measured using grains (gr). One pound equals 7000 grains.

Depending on the bullet, its mass can be anywhere from 15 gr (0.002143 lbs or 0.972 g) to over 600 gr (0.0857 lbs or 38.879 g).

While subsonic bullets exist, many bullets are supersonic — they travel faster than the speed of sound (1130 f/s or 343 m/s). Rifle bullets leave the muzzle as fast as 2730 mph (4004 ft/s or 1220 m/s)! The following sections will help you understand why such small bullets can pack quite the punch when fired at these insane speeds!

🔎 Are you curious about what kind of recoil you'll have to deal with? Head straight to our recoil energy calculator!

Formula to calculate bullet energy

We can calculate the bullet's kinetic energy using the formula:

E = \frac{1}{2}\cdot m \cdot v^2

where:

$E$ — Bullet's kinetic energy;
$m$ — Mass of the bullet; and
$v$ — Velocity of the bullet.

The SI unit for bullet energy (kinetic energy) is joules (J). In the US, foot-pound (ft-lbf or ft-lbs) is widely used to express bullet energy. We've already observed that bullet mass is commonly given in grains. Bullet speeds can be measured in feet per second (ft/s) or meters per second (m/s), although miles per hour (mph) and kilometers per hour (km/h) could also be used.

⚠️ The pound in foot-pound refers to pound-force, a unit of force. You should NOT confuse it with avoirdupois pound, a unit of mass. In fact, one pound-force is the product of one avoirdupois pound and the gravitational acceleration (32.174049 ft/s²). So, one pound-force equals 32.174049 lb-ft/s².

In the next section, we shall attempt to show you how to handle unit conversions when you're calculating bullet kinetic energy.

How to calculate bullet energy in ft-lbs

Say you have bullet mass in grains and velocity in foot per second. Let's note some unit conversion facts:

$1 \text{ lb} = 7000 \text{ gr}$
$1 \text{ lbf} = 32.174049 \text{ lb-ft/s}^2$

Now we are ready to use our bullet energy formula to calculate bullet energy in ft-lbs (or ft-lbf):

\begin{align*} E &= \frac{1}{2}\cdot m \text{ (gr)} \cdot v^2 \text{ (ft}^2/\text{ s}^2)\\[1.3em] &= \frac{1}{2}\cdot \frac{m \text{ (lb)}}{7000} \cdot v^2 \text{ (ft}^2/\text{ s}^2)\\[1.3em] &= \frac{1}{2}\cdot \frac{m}{7000} \cdot v^2 \text{ (ft} \cdot \text{ lb-ft}/\text{ s}^2)\\[1.3em] &= \frac{1}{2}\cdot \frac{m}{7000} \cdot v^2 \frac{\text{lbf}}{32.174049} \text{ ft}\\[1.3em] &=\frac{m \cdot v^2}{2 \cdot 7000 \cdot 32.174049} \text{ ft-lbf}\\[1.3em] E &= \frac{m \cdot v^2}{450436.686} \text{ ft-lbf} \end{align*}

Note that $m$ is in grains, and $v$ is in feet per second in the above formula.

🔎 When you need to convert foot-pounds to joules, remember the conversion factor $1 \text{ ft-lb} = 1.355818 \text{ J}$ .

Example calculation of bullet kinetic energy

Let's look at how to calculate bullet energy with an example: Say you have two kinds of rounds for a 9 mm pistol: HST 124 grain and HST 147 grain. The 124 gr bullet has a muzzle velocity of 1150 ft/s while the 147 gr bullet fires with 1000 ft/s muzzle velocity. Let us see which shot has higher muzzle energy.

Calculating the bullet energy in ft-lbs for HST 124 gr:

\begin{align*} E &= \frac{m \cdot v^2}{450436.686} \text{ ft-lbf}\\[1em] &= \frac{124 \cdot 1150^2}{450436.686} \text{ ft-lbf}\\[1em] &= \frac{163990000}{450436.686} \text{ ft-lbf}\\[1em] E &\approx 364.068 \equiv 364.1 \text{ ft-lbf} \end{align*}

Similarly, let us calculate the muzzle energy of the HST 147 gr bullet:

\begin{align*} E &= \frac{m \cdot v^2}{450436.686} \text{ ft-lbf}\\[1em] &= \frac{147 \cdot 1000^2}{450436.686} \text{ ft-lbf}\\[1em] &= \frac{147000000}{450436.686} \text{ ft-lbf}\\[1em] E &\approx 326.3499 \equiv 326.35 \text{ ft-lbf} \end{align*}

So, the HST 124 gr rounds have a higher bullet energy than the HST 147 gr rounds. The 23-grain weight advantage that allows the HST 124 gr rounds to fire 150 ft/s faster makes a difference!

Calculating muzzle energy and terminal energy

The bullet's kinetic energy is not constant throughout its trajectory, even when there are no obstacles, as its speed reduces due to air resistance. The two most points of interest in a bullet's trajectory are, of course, the gun's muzzle (the starting point) and the target:

When we measure the bullet's velocity as it leaves the gun's muzzle, we call it muzzle velocity. Using this in the bullet energy calculation formula gives us muzzle bullet energy (or simply, muzzle energy). This will help you determine the gun's recoil behavior!
The velocity at which the bullet hits its target is called its terminal velocity. The bullet energy at terminal velocity is its terminal bullet energy (or terminal energy). This energy is transferred to the target on impact and will determine the bullet's terminal ballistics.

🙋 Other factors, such as the bullet's shape and type, also affect its terminal ballistics.

We can calculate muzzle energy and terminal energy using the same bullet energy formula — we need to use the proper velocity.

Using this bullet energy calculator

Our bullet energy calculator is quick and easy to use:

Enter the bullet mass in grains or any unit you prefer (select the unit first).
Provide the bullet velocity in feet per second or any unit you wish.
The calculator will show you the bullet energy in foot-pounds. You can also see it in joules by changing the unit.

Are you enjoying our calculator? If you're interested in projectiles like bullets, you will love our projectile motion calculator!

FAQs

How do you calculate foot-pounds of energy for bullets?

To calculate a bullet's energy in foot-pounds, follow these steps:

Multiply the bullet's velocity (v) in foot per second by itself to obtain the velocity squared.
Multiply this result with the bullet's mass (m) in grains.
Divide this result by 450436.686 to obtain the bullet's energy (E) in foot-pounds:

E = (m ⋅ v²)/450436.686 ft-lbs

Or you can skip the tedious calculations and unit conversions using our bullet energy calculator!

How do you calculate bullet energy at 100 yards?

A bullet may lose anywhere between 20-30% of its velocity by the first 100 yards. To accurately calculate the bullet energy at 100 yards, you must measure its velocity (v₁₀₀) at this point. Using this in the bullet energy equation, we'll get the bullet energy (E₁₀₀) (in ft-lbs):

E₁₀₀ = (m ⋅ v²₁₀₀)/450436.686

What is the muzzle energy of a .338 Lapua Magnum at 3000 ft/s?

A .338 Lapua Magnum round with a bullet weight of 250 grains will have a bullet energy of 4995 ft-lbs (6773 J) at 3000 ft/s. To arrive at this answer, follow these steps:

Multiply the bullet's velocity itself to obtain the velocity squared:

v² = 3000² = 9,000,000 ft²/s²
Multiply this result with the bullet's mass:

m ⋅ v² = 250 ⋅ 9,000,000 = 2,250,000,000
Divide this result by 450436.686 to obtain the bullet's energy (E) in foot-pounds:

E = 2,250,000,000/450436.686 ≈ 4,995.15 ≡ 4995 ft-lbs

How does barrel length affect muzzle velocity?

If everything else remains the same, a longer barrel length will allow the propellant gas to act on the bullet longer, thus accelerating it to higher speeds before exiting the muzzle.

However, the propellant gas will start to lose pressure as it expands. So if the barrel is too long, the gas pressure cannot propel the bullet any further, and the friction between the bullet and the chamber will start to reduce its speed!