Bug-Rivet Paradox

Q: Is causality violated in the bug-rivet paradox?

The bug-rivet paradox does not violate casualty — to be fair, as far as we know, causality can't be violated at all. The apparent change in the order of events, as seen from the different frames of reference, is solved by understanding that information about events takes time to travel along the length of the rivet. Read more

Q: What is length contraction?

Length contraction is a consequence of time dilation . Both are relativistic phenomena associated with the existence of a "speed limit" for the Universe, which corresponds to the speed of light. As the speed of light must be constant in all reference frames, objects that travel at speeds close to the one of light experience subjective time dilation to allow light to travel at the proper speed in their frame of reference too. Read more

Created by Davide Borchia

Reviewed by Steven Wooding

Last updated: Jan 18, 2024

Table of contents:

The bug-rivet paradox is an intriguing problem in relativity that challenges our understanding of how Nature works. Keep reading: in this article, you will:

Learn about relativity paradoxes: the bug-rivet paradox as an example of the quirkiness of relativity;
See the bug-rivet paradox from the bug's perspective and the rivet's perspective;
Encounter an apparent paradox and resolution of the bug-rivet paradox.

Ready? Let's squish — or not — some bugs!

The fundamentals of relativity for the bug-rivet paradox

The bug-rivet paradox is strictly a relativistic problem. When objects start moving at a noticeable fraction of the speed of light, we begin witnessing some exciting phenomena. Among them, length contraction is of major importance.

Length contraction stems from time dilation, a relativistic effect caused by the existence of a "speed limit" in the Universe, the speed of light. As objects approach the speed of light, $c$ , their time, as seen from a stationary frame of reference (stationary in relation to the moving object), would slow down, eventually freezing when the moving objects reach $c$ . To compensate for this time dilation, length contracts.

🙋 We talked in detail about these two relativistic phenomena at the length contraction calculator and the time dilation calculator!

The speed of light is also the speed limit of information in our Universe. Nothing, not even the "concept" of an event, can travel faster than light. This will have important consequences in the resolution of the bug-rivet paradox. As per our current understanding of Nature, this speed limit prevents anything superluminal: no quantum entanglement-based phones, no faster-than-light spaceships, and, we'd like to stress this, no time travel!

Setting up the bug-rivet paradox

The bug-rivet paradox begins with a simple setup. Take a rivet with shaft length $a$ and a hole with length $L$ . As an initial condition, we set that the rivet is shorter than the hole: $L\gt a$ . The rivet has a head larger than the hole that would stop its run once it hits the hole. At the bottom of the hole, we find a blissfully unaware bug that has negligible dimensions since we are playing physics.

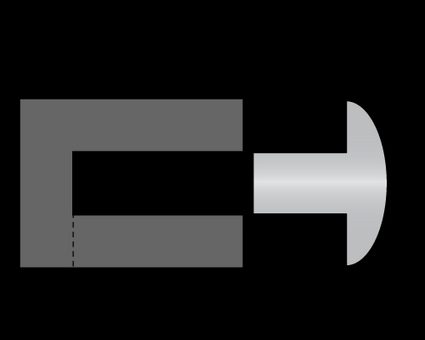
Now take the rivet, and assume it's traveling at relativistic speed toward the hole, perfectly aligned and ready to strike. Should our bug start writing its will? Will the rivet squish it, or will physics spare it? In our daily experience, the answer would be straightforward: as the rivet is shorter than the hole, the bug will survive. However, Einstein is here to change the game's rules.

Let's start by introducing some essential quantities. First, the speed at which the rivet is moving:

v = \beta c

where:

$v$ — Rivet's speed;
$c$ — Speed of light: $c = 299,\!792,\!458 \ \mathrm{m/s}$ ; and
$\beta$ — Ratio of the two speeds.

Be sure to hold tight to the concept of $\beta$ as a measure of the object's speed: $\beta = v/c$ is the fraction of the speed of light at which the object moves.

We can also introduce the famous Lorentz's factor, $\gamma$ :

\frac{1}{\gamma} = \sqrt{1-\beta^2}

Let's dive into the bug-rivet paradox. First stop: the bug!

Let's hang out with the bug: stationary frame of reference

The bug is stationary; thus, in its frame of reference, the rivet is zooming in its direction at speed $v$ . The bug, however, is relatively chill if we neglect the energy that would be dissipated in the impact: at rest, the rivet would not hit it, and thanks to relativistic effects, the rivet looks shrank to a shorter length (length contraction). The bug sees the rivet as a contracted version with the length:

a_\mathrm{app} = \frac{a}{\gamma} = a\cdot\sqrt{1-\beta^2}

Of course, $a_\mathrm{app}\lt a\lt L$ .

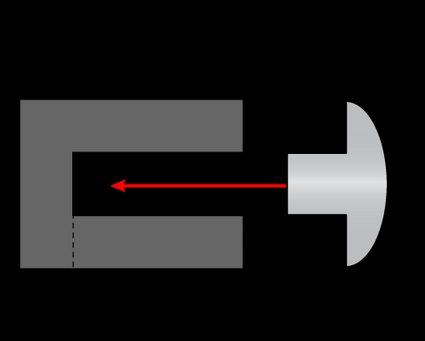
The traveling rivet is shortened to a safe length for the bug.

However, our bug didn't take into account the issue of rigidity. It failed to assume that the contracted rivet would stop once the head hits the wall of the hole where it shelters. What would happen, instead? Let's follow the events step-by-step:

The rivet enters the hole, penetrating it for a length $a/\gamma$ .
After this initial moment, the rivet's head hits the wall. The rivets head immediately halts to a stop.
The rivet's tip, however, keeps moving: the information of the impact doesn't reach it immediately!
After the necessary time elapses, the information of the impact reaches the tip of the rivet, which also comes to a stop.

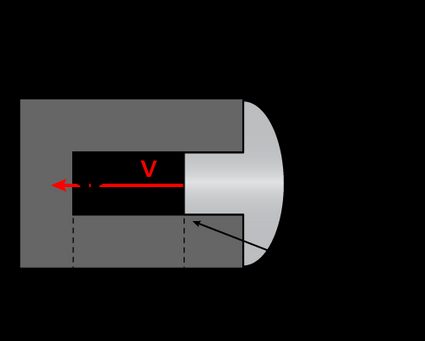
The tip of the rivet keeps moving after the impact: the body is not rigid anymore!

The time required for the information to travel down the shaft is:

t_\mathrm{stop, bug} = \frac{a}{\gamma}\frac{1}{c-v} =\frac{a}{\gamma c (1-\beta)}

During this time, as we assume the bug is sweating bullets, the tip keeps moving for a further distance $d_\mathrm{tip}$ :

d_\mathrm{tip} = v\cdot t_\mathrm{stop, bug}

Is there a situation where the bug is squished? We need to set up an inequality:

d_\mathrm{tip}\gt L-\frac{a}{\gamma}

The left-hand side is the distance traveled by the tip. The right-hand side is the fraction of the hole that separates the tip at the moment of the impact of the rivet's head and the bug. Let's expand this inequality:

\begin{split} \frac{\beta c a}{\gamma c (1-\beta)}&\gt L-\frac{a}{\gamma}\\[1em] \frac{a}{\gamma}+\frac{\beta \cancel{c} a}{\gamma \cancel{c} (1-\beta)}&\gt L\\[1em] \frac{a}{\gamma}\left(\frac{\beta}{1-\beta}+1\right)&\gt L\\[1em] \frac{a}{\gamma}\left(\frac{\cancel{\beta}+1-\cancel{\beta}}{1-\beta}\right)&\gt L \end{split}

Using the definition of $\gamma$ , we write:

\begin{split} \frac{1}{\gamma(1-\beta)}&=\frac{\sqrt{1-\beta^2}}{1-\beta}\\[1em] &=\frac{\sqrt{\cancel{(1-\beta)}(1+\beta)}}{\sqrt{1-\beta}\cancel{\sqrt{1-\beta}}}\\[1em] & = \frac{\sqrt{1+\beta}}{\sqrt{1-\beta}} \end{split}

Neat! Let's substitute this result in the previous inequality:

\begin{split} \frac{a}{\gamma}\left(\frac{1}{1-\beta}\right)&\gt L\\[1em] a\frac{\sqrt{1+\beta}}{\sqrt{1-\beta}}&\gt L\\[1em] \frac{a}{L}&\gt \frac{\sqrt{1-\beta}}{\sqrt{1+\beta}} \end{split}

As we want to find a velocity for which the bugs may get squished, we try to isolate $\beta$ in the previous inequality:

\begin{split} \left(\frac{a}{L}\right)^2&\gt \frac{1-\beta}{1+\beta}\\[1em] \left(\frac{a}{L}\right)^2(1+\beta)&\gt 1-\beta\\[1em] \left(\frac{a}{L}\right)^2+\beta\left(\frac{a}{L}\right)^2&\gt 1-\beta\\[1em] \beta\left(1+\left(\frac{a}{L}\right)^2\right)&\gt 1-\left(\frac{a}{L}\right)^2\\[1em] \beta&\gt \frac{1-\left(\frac{a}{L}\right)^2}{1+\left(\frac{a}{L}\right)^2} \end{split}

We define a threshold value $\beta_\mathrm{c1}$ :

\beta_\mathrm{c1} = \frac{1-\left(\frac{a}{L}\right)^2}{1+\left(\frac{a}{L}\right)^2}

If the rivet travels at speeds higher than the threshold value, the bug gets squished as the tip of the rivet reaches it before the information about the impact. On the other hand, if the speed is lower than $\beta_\mathrm{c1}$ , the bug is safe, though, for sure, scared!

The look of things from the frame of reference of the rivet

Let's change our point of view: we are now traveling with the rivet at relativistic speed. Due to the nature of inertial reference frames, from the rivet point of view, it's the hole that is moving, closing in on with speed $v$ . Consequently, the rivet sees a hole contracted in length.

Uh-oh: these are not good news for our bug, which is now threatened by what is, effectively, a prolonged rivet. In this frame of reference, we can identify a critical speed at which the rivet hits the hole tip first, thus squishing the poor bug in the process. How do we determine this speed? First, let's find the length of the hole from the rivet's point of view:

L_\mathrm{app} = \frac{L}{\gamma}

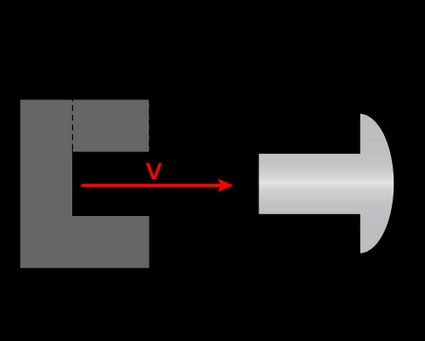
The hole can shrink at length shorter than the rivet's shaft: the consequences are dramatic.

The bug doesn't have a chance if the rivet's shaft is longer than this contracted length:

\begin{split} \frac{L}{\gamma}&\lt a\\[1em] \sqrt{1-\beta^2}&\lt \frac{a}{L}\\[1em] 1-\beta^2&\lt \left(\frac{a}{L}\right)^2\\[1em] \beta^2&\gt 1-\left(\frac{a}{L}\right)^2\\[1em] \beta&\gt \sqrt{1-\left(\frac{a}{L}\right)^2} \end{split}

We found another critical speed, defined by:

\beta_\mathrm{c2}=\sqrt{1-\left(\frac{a}{L}\right)^2}

Notice how this speed is higher than the critical one we found for the bug's frame of reference. This is an extreme case where we sense a paradox. How would this situation pan out from the bug's point of view? We imagine that the contracted rivet's head would hit first, followed by the still-moving tip, waiting for the information about the impact to reach it.

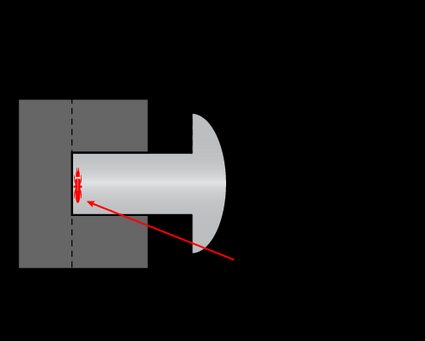
The tip hits first, apparently switching order of the events.

From the rivet's point of view, the tip hits first. The paradox (or lack thereof) lies in our affection for simultaneousness: when relativity affects our world, the speed at which information travels matters. Imagine a rivet traveling exactly at the critical speed defined by $\beta_\mathrm{c2}$ . In the rivet's frame of reference, the impact of the tip with the bug and the impact of the head with the hole's surface happen simultaneously. From the bug's point of view, these events are not simultaneous anymore: the rivet is not a rigid object anymore.

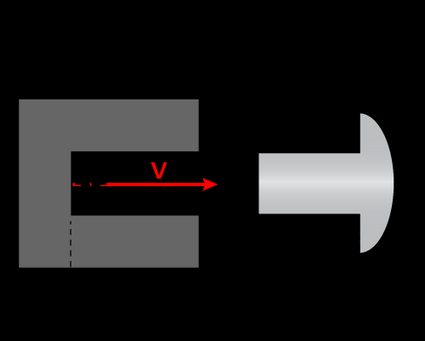
Reducing the speed may put ourselves in a less ambiguous situation.

Is there a situation where we can avoid this apparent paradox? Yes: consider a situation where the rivet's shaft length $a$ is still shorter than the length of the length-contracted hole. In this situation, the rivet tip enters the hole, and then the head slams into the wall, beginning the stopping process. In the rivet's frame of reference, the bottom of the rivet won't receive the information about the impact for an additional interval of time, during which the bottom of the hole will apparently keep moving, along with the bug, in the direction of the rivet's tip. This time is $t_2$ :

t_2 = \frac{a}{c}

The distance covered by the poor bug during $t_2$ is:

vt_2= \beta \cancel{c} \frac{a}{\cancel c}=\beta a

Let's find the speed for which this distance would cause the bug's permanent demise by setting up the following inequality:

vt_2\gt \frac{L}{\gamma}-a

Let's work our way till we can isolate $\beta$ :

\begin{split} \beta a&\gt \frac{L}{\gamma}-a\\[1.3em] a(1+\beta)&\gt \frac{L}{\gamma}\\[1.3em] a(1+\beta)&\gt L\sqrt{1-\beta^2}\\[1.3em] \frac{1+\beta}{\sqrt{1-\beta^2}}&\gt \frac{L}{a}\\[1.3em] \frac{\sqrt{1+\beta}}{\sqrt{1-\beta}}&\gt \frac{L}{a}\\[1.3em] \frac{1-\beta}{1+\beta}&\lt \left(\frac{a}{L}\right)^2\\[1.3em] 1-\beta&\lt \left(\frac{a}{L}\right)^2(1+\beta)\\[1.3em] \beta&\gt \frac{1-\left(\frac{a}{L}\right)^2}{1+\left(\frac{a}{L}\right)^2} \end{split}

We identify a critical value of $\beta$ for which the bug remains safe. Notice that it's the same value we found in the bug's frame of reference:

\beta_\mathrm{c1} = \frac{1-\left(\frac{a}{L}\right)^2}{1+\left(\frac{a}{L}\right)^2}

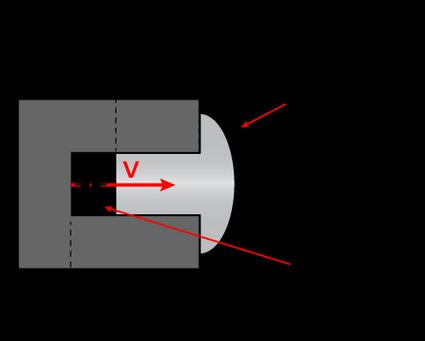
The bug keeps moving until it squishes against the bottom of the rivet.

Who is right? The resolution of the bug-rivet paradox

The solution to the bug-rivet paradox is relatively (😉) straightforward after we accept the quirkiness of relativity. We found that in both the bug's and the rivet's frame of reference, we can identify a critical speed that separates the instances where the bug survives the impact and the instances where the squish happens.

However, for speeds high enough, we can identify a region spanning from the value $\beta_{\mathrm{c2}}$ to $c$ where, in the rivet's reference frame, the impact with the bug happens before the impact of the rivet's head with the wall. Notice that this is not an actual problem: the impact happens before the information about the head's impact reaches the tip: it appears to us that the head impacted first, but from the bug's point of view, the violent impact with the tip happens before it can understand that the tip reached the wall: we preserved the cause-effect order!

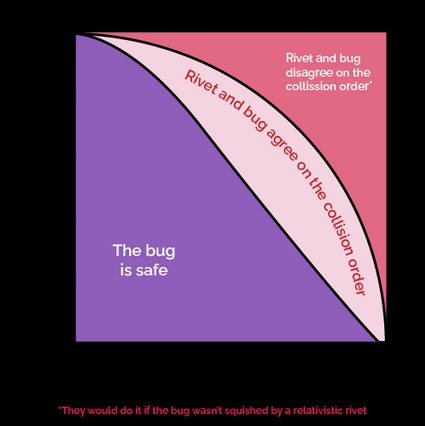
The three situations we encounter while dealing with the bug-rivet paradox.

The graph above shows the three situations we encountered in the bug-rivet paradox. Under the lower curve, the combination of the ratio of the rivet and hole length and the speed of the rivet allows the bug to come out unscathed. Between the two curves, we find a region where, in both frames of reference, the rivet's head hits the hole's wall first, followed immediately by the impact of the rivet's tip with the bug.

Above the second line (in the red zone), the frames of reference appear to disagree on the order of the impacts. For the rivet, the impact with the bug happens first; in the bug's frame of reference, the head hits first. However, as information needs time to reach the rivet's tip, and consequently, the bug gets squished before knowing that the head hit the wall.

🙋 With our relativistic kinetic energy calculator, you can find that the energy of the impact of a $3\ \mathrm{g}$ rivet traveling at $0.8c$ would liberate $40\ \mathrm{kT}$ of energy, the yield of a large tactical nuclear weapon. We are pretty sure that you got rid of the bug.

An example of the bug-rivet paradox

Let's give some numbers to our math! Our bug lies at the bottom of a $7\ \mathrm{cm}$ hole. Take a $5\ \mathrm{cm}$ long rivet traveling at a relativistic speed.

Let's put ourselves in the bug's frame of reference. We can calculate the critical $\beta$ (hence, the speed) at which the rivet must travel to manage to squish that bug:

\begin{split} \beta_\mathrm{c1} &= \frac{1-\left(\frac{a}{L}\right)^2}{1+\left(\frac{a}{L}\right)^2}\\[1.5em] &=\frac{1-\left(\frac{5\ \mathrm{cm}}{7\ \mathrm{cm}}\right)^2}{1+\left(\frac{5\ \mathrm{cm}}{7\ \mathrm{cm}}\right)^2}= 0.3243 \end{split}

If the rivet travels at a speed lower than $0.3243c$ , the bug can breathe a sigh of relief: it's safe. Any speed higher than that, and the bug would get squished. In this frame of reference, the head of the rivet always hits first.

Let's change the frame of reference: from the rivet's perspective, the maximum speed at which the bug is safe is still $0.3243c$ . However, as we get closer to the speed of light, the apparent length of the hole contracts to the point that the end of the rivet would apparently hit the bug before the head hits the wall. The speed at which this happens is defined by the value of $\beta$ :

\begin{split} \beta_\mathrm{c2}&=\sqrt{1-\left(\frac{a}{L}\right)^2}\\[1.5em] &=\sqrt{1-\left(\frac{5\ \mathrm{cm}}{7\ \mathrm{cm}}\right)^2}=0.6999 \end{split}

Above $0.6999c$ , the two frames of reference disagree on the order of the impacts.

FAQ

What is the bug-rivet paradox?

The bug-rivet paradox is a paradox in relativity that sees an apparent violation of causality (order) of the events in a situation where a rivet moving at relativistic speeds impacts a hole longer than the rivet's length. Due to the relativistic effect, there are situations where even though the rivet is shorter than the hole, the time required by information to travel across the rivet may cause the tip of the rivet to reach the end of the hole after its head stops at the wall. In extreme cases, the order of the impacts may appear reversed.

Can we find a solution to the bug-rivet's paradox?

The bug-rivet paradox is easily solved by understanding the rules controlling the behavior of objects moving at relativistic speed. The paradox states that the order of the impacts (rivet's head-hole's wall, rivet's tip-bug) changes above a certain speed. However, if we consider that the information about the head-wall impact takes a given time to reach the tip, we see that in both frames of reference, from the observer's point of view, the tip hits first.

Is causality violated in the bug-rivet paradox?

The bug-rivet paradox does not violate casualty — to be fair, as far as we know, causality can't be violated at all. The apparent change in the order of events, as seen from the different frames of reference, is solved by understanding that information about events takes time to travel along the length of the rivet.

What is length contraction?

Length contraction is a consequence of time dilation. Both are relativistic phenomena associated with the existence of a "speed limit" for the Universe, which corresponds to the speed of light. As the speed of light must be constant in all reference frames, objects that travel at speeds close to the one of light experience subjective time dilation to allow light to travel at the proper speed in their frame of reference too.

Davide Borchia

Set-up

Length of rivet (a)

Length of the hole (L)

Speed (v)

Speed ratio (ß)

Lorentz factor (γ)

Frame of reference

Rivet frame of reference

Apparent hole length

Time before the rivet hole stops (t₂)

Distance (apparently) traveled by the bug

ß for direct squish

Critical ß

How is the bug?

Electron speedE = mc²Gravitational time dilation… 5 more