Last updated: May 27, 2024

Angle of Incidence Calculator

Q: How do I calculate angle of incidence?

To calculate the angle of incidence: Find the refractive indices of the two media involved. Divide the refractive index of the second medium by the refractive index of the first medium. Multiply the quotient by the sine of the angle of refraction to obtain the incident angle.

Table of contents

What is angle of incidence?Using the angle of incidence calculator.Other related calculators FAQs

The angle of incidence calculator is useful to determine the incident angle for a light ray using Snell's law. The article accompanying the calculator will explain what incident angle is and how to calculate it.

What is angle of incidence?

The angle of incidence refers to the angle at which a light ray incidents on the surface of a medium. As per Fermat's principle, a light ray always travels the path that takes the least time. The speed of light varies as per the medium. Light, when moving from one medium to another, changes direction. This phenomenon is refraction. Not just light, other types of waves like sound and water waves also exhibit refraction.

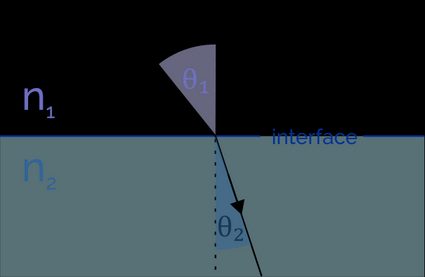
Snell's law, or the law of refraction, helps us determine the change in direction by calculating the angle of refraction. The angle of refraction is the angle by which the light ray has changed direction upon entering the medium. Consider a light ray incident upon a medium at an angle $\theta_1$ , the angle of refraction, $\theta_2$ is:

\sin{\theta_1} = \sin{ \theta_2} \frac{n_2}{n_1}

where:

$n_1$ - Refractive index of medium 1; and
$n_2$ - Refractive index of medium 2.

In other words, the ratio of sines of the incident and refraction angle is equal to the ratio of refractive indices.

Using the angle of incidence calculator.

Let's calculate the angle of incidence for a light ray refracting out of a water body at 45° to understand how to calculate the angle of incidence.

Select air as medium 1.
Select water as medium 2.
Enter the angle of refraction as 45°.
The angle of incidence is:

\qquad \scriptsize \begin{align*} \theta_1 &= \sin^{-1} \left ( \sin{ \theta_2} \frac{n_2}{n_1} \right ) \\ \theta_1 &= \sin^{-1} \left ( \sin{45} \frac{1.333}{1.000273} \right ) \\ \theta_1 &= 70.4442^\circ \end{align*}

FAQs

How do I calculate angle of incidence?

To calculate the angle of incidence:

Find the refractive indices of the two media involved.
Divide the refractive index of the second medium by the refractive index of the first medium.
Multiply the quotient by the sine of the angle of refraction to obtain the incident angle.

What is the refractive index of air?

The refractive index of air is 1.000273 at standard temperature and pressure. This value is slightly higher than the refractive index of vacuum, which is set to 1 by definition.

What is the angle of incidence for light passing through glass and refracted to 30°?

The angle of the incident for the light ray, in this case, is 49.4459°. Considering the refractive index of air and glass as 1.000273 and 1.52, respectively. Such that, sin(theta1) = sin(theta2) × n2 / n1 = = sin(30°) × 1.52 / 1.000273 = 49.4459°.