Floating-Point Calculator

The floating-point calculator is here to help you understand the IEEE754 standard for the floating-point format. It acts as a converter for floating-point numbers — it converts 32-bit floats and 64-bit floats from binary representations to real decimal numbers and vice versa.

Before we get into the bits and bytes of the float32 and float64 number formats, let's learn how the floating-point calculator works. Just follow these easy steps:

1. If you want to convert the binary encoding of a floating-point number to the decimal number it represents, select floating-point to number at the top of the calculator. Then:

   • Select the precision used. This determines how your binary representation will be interpreted.

   • Enter the floating-point number's binary digits. You can enter the sign, exponent, and fraction separately, or you can enter the entire bit-string in one go — select your preference in the Bit input method dropdown menu.

   • The value stored in your float will be shown at the bottom of the calculator.

2. If you want to convert a value into its floating-point representation, select number to floating-point at the top of the calculator. Then:

   • Enter your number in the field below that.

   • The IEEE754 floating-point binary and hexadecimal representations of both single- and double-precision floats will be shown below.

   • The floating-point calculator will also show you the actual value stored due to the loss of precision inherent to the floating-point format. The error due to this loss of precision will also be reported.

In computing, a floating-point number is a data format used to store fractional numbers in a digital machine. A floating-point number is represented by a series of bits (1s and 0s). Computers perform mathematical operations on these bits directly instead of how a human would do the math. When a human wants to read the floating-point number, a complex formula reconstructs the bits into the decimal system.

The IEEE754 standard (established in 1985 by the Institute of Electrical and Electronics Engineers) standardized the floating-point format and also defined how the format can be operated upon to perform math and other tasks. It's been widely adopted by hardware and software designers and has become the de facto standard for representing floating-point numbers in computers. When someone mentions "floating-point numbers" in the context of computing, they'd generally mean the IEEE754 data format.

The most well-known IEEE754 floating-point format (single-precision, or "32-bit") is used in almost all modern computer applications. The format is highly flexible: float32s can encode numbers as small as 1.4×10⁻⁴⁵ and as large as 3.4×10³⁸ (both positive and negative).

Besides single-precision, the IEEE754 standard also codifies double-precision ("64-bit" or float64), which can store numbers from 5×10⁻³²⁴ to 1.7×10³⁰⁸. Less commonly used IEEE754 formats include:

• Half-precision ("16-bit");
• Quadruple-precision ("128-bit"); and
• Octuple-precision ("256-bit").

However, a floating-point number is not just a number converted to the binary number system — it's much more complicated than that! Let's learn how the IEEE754 floating-point standard works.

Any floating-point binary representation consists of three segments of bits: sign, exponent, and fraction.

• The sign (S) indicates positive or negative;
• The exponent (E) raises 2 to some power to scale the number; and
• The fraction (F) determines the number's exact digits.

The segments' lengths and exact formula applied to S, E, and F to recreate the number depend on the format's precision.

When stored in memory, $S$, $E$, and $F$ are laid end-to-end to create the full binary representation of the floating-point number. In computer memory, it might look like this:

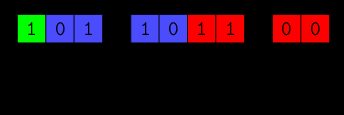
These bits are what the computer manipulates when arithmetic and other operations are performed. The computer never sees a number as its decimal digits — it only sees and works with these bits.

Let's look at the two most commonly used floating-point formats: float32 and float64.

float32 is the most commonly used of the IEEE754 formats. As suggested by the term "32-bit float", its underlying binary representation is 32 bits long. These are segmented as follows:

• 1 bit for the sign ($S$);
• 8 bits for the exponent ($E$); and
• 23 bits for the fraction ($F$).

When it's stored in memory, the bits look like this:

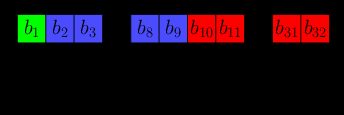
We can rewrite it as a binary string:

The real value that this 32-bit float stores can be calculated as:

where:

• $127$ is called the exponent bias and is inherent to the single-precision format;
• $x_2$ means that $x$ must be interpreted as if in base 2 or binary; and
• $(1.b_{10}...b_{32})_2$ means to take the binary bits $b_{10}$ to $b_{32}$ and use it as the fractional part of $1$ to form a binary fraction. See our binary fraction calculator for help on that.

We can rewrite the formula better using $S$, $E$, and $F$:

where

• $S = b_1$;
• $E = (b_2\ ...\ b_9)_2$; and
• $F = (b_{10}\ ...\ b_{32})_2$.

To let floating-point formats store really small numbers with high precision, $E=0$ and $F>0$ activates a separate formula. For float32, that formula is

Numbers created by this formula are called "subnormal numbers", while "normal numbers" are created using the previous formula.

There are other special cases, encoded by specific values for $E$ and $F$:

$\text{NaN}$ means "not a number", which is returned when you divide by zero or perform impossible math using infinity. For the cases of $\pm 0$ and $\pm \infty$, the sign bit determines whether the number is positive or negative. And yes, negative zero is a thing!

An example

Let's convert the binary floating-point representation 01000001110111100000000000000000 to the real number it represents.

1. First, let's segment it into $S$, $E$, and $F$:

   • $S = 0_2 = 0$

   • $E = 10000011_2 = 131$

   • $F = 10111100000000000000000_2$

2. Since $0<E<255$, we use the normal number formula:

   $(-1)^S \times 2^{E-127} \times (1.F)_2$

   • $(-1)^S = 1$ (so the number is positive!)

   • $2^{E-127} = 2^{4} = 16$

   • $(1.F)_2 = 1.101111_2 = 1.734375$

3. Combine the three multiplicands:

   $1 \times 16 \times 1.734375 = \textbf{27.75}$

Want to see for yourself? Try this value in our floating-point calculator to see it in action!

Note that $01000001110111100000000000000000_2$ converted directly from binary to decimal is not $27.75$, but $1,\!105,\!068,\!032$. Quite the difference, wouldn't you say?

The inner workings of the float64 data type are much the same as that of float32. All that differs are:

• The lengths of the exponent and fraction segments of the binary representation — in 64-bit floats, $E$ takes up 11 bits, and $F$ takes up 52.
• The exponent bias — in 64-bit floats, it's 1023 (whereas in 32-bit floats, it's 127).

The formulas for the reconstruction of 64-bit normal and subnormal floating-points are, therefore, respectively:

and

Because of the additional exponent and fraction bits compared to float32s, float64s can store much larger numbers and at much higher accuracy.

To convert a decimal number to a floating-point representation, follow these steps:

1. Convert the entire number to binary and then normalize it, i.e. write it in scientific notation using base 2.
2. Truncate the fraction after the decimal point to the allowable fraction length.
3. Extract the sign, exponent, and fraction segments.

Refer to the IEEE754 standard for more detailed instructions.

An example

Let's convert $27.75$ back to its floating-point representation.

1. Our integer part is $27$, which in binary is $11011_2$. Our fraction part is $0.75$. Let's convert it to a binary fraction:

   • $0.75 \times 2 = 1.50 = \textbf{1} + 0.5$

   • $0.5 \times 2 = 1.00 = \textbf{1} + 0$

   So $0.75 = 0.11_2$, and then $27.75 = 11011.11_2$. To normalize it, we rewrite it as:

2. The digits after the decimal point are already a suitable length — for float32, we'd be limited to 23 bits, but we have only five.

From the normalized rewrite, we can extract that:

• $S = 0$, since the number is positive;
• $E = \textcolor{blue}{4}+127 = 10000011_2$ (we add $127$ because $E-127$ must be $\textcolor{blue}{4}$); and
• $F = \textcolor{red}{101111}00000000000000000$ (zeroes get padded on the right because we're dealing with fractional digits and not an integer).

Therefore, our floating-point representation is $0\textcolor{blue}{10000011}\textcolor{red}{101111}00000000000000000$.

You can verify this result with our floating-point calculator!

Floating-point numbers cannot represent all possible numbers with complete accuracy. This makes intuitive sense for sufficiently large numbers and for numbers with an infinite number of decimals, such as pi ($\pi$) and Euler's number ($e$). But did you know that computers cannot store a value as simple as $0.1$ with 100% accuracy? Let's look into this claim!

When you ask a computer to store $0.1$ as a float32, it will store this binary string:

00111101110011001100110011001101

If we convert that back to decimal with the floating-point formulas we learned above, we get the following:

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001101_2$

That's a little bit more than $0.1$! The error (how far away the stored floating-point value is from the "correct" value of $0.1$) is $1.49 \times 10^{-9}$.

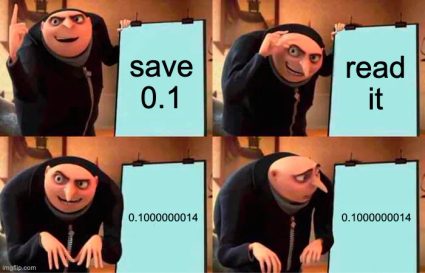
Let's try to rectify this mistake and make the smallest change possible. Our stored number is a little too big, so let's change that last bit from a $1$ to a $0$ to make our float a little bit smaller. We're now converting:

00111101110011001100110011001100

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001100_2$

And we've missed our mark of $0.1$ again! This time, the error is a little larger ($5.96\times 10^{-9}$). The first binary string that ended in 1 was even more correct than this one!

You may think, "what if we used more bits?" Well, if we were to do the same with the float64 format instead, we'd find the same problem, although less severe. $0.1$ converted to a 64-bit floating-point and back to decimal is $0.100000000000000006$, and the error here is $5.55 \times 10^{-18}$. This is the higher accuracy of float64 in action, but the error is still not $0$ — the conversion is still not lossless.

This is, unfortunately, the drawback of the ubiquitous floating-point format — it's not 100% precise. Small bits of information get lost, and they can wreak havoc if not accounted for. The only numbers that can be stored perfectly as a float without any losses are powers of 2 scaled by integers because that's how the format stores numbers. All other numbers are simply approximated when stored as a floating-point number. But it's still the best we've got!

The IEEE754 floating-point format standard enables efficient storage and processing of numbers in computers.

• From a hardware perspective, many simplifications of floating-point operations can be made to significantly speed up arithmetic, thanks to the IEEE754 standard's specifications.

• For software, floats are very precise and typically lose a few millionths (if not less) per operation, which enables high-precision scientific and engineering applications.

The floating-point representation of 12.25 is 01000001010001000000000000000000. Its sign is 0, its exponent is 10000010₂ = 130, and its fraction is 100010...0. Reconstructed to decimal, we get:

(−1)⁰ × 2^(130−127) × (1.10001)₂
= 1 × 2³ × 1.53125
= 12.25