Volume of a Hemisphere Calculator

This volume of a hemisphere calculator quickly finds the volume of a hemisphere with six different equations. Do you need to solve a specific problem but don't know how to find the volume of a hemisphere? Try entering one of the parameters and see how simply this calculator works.

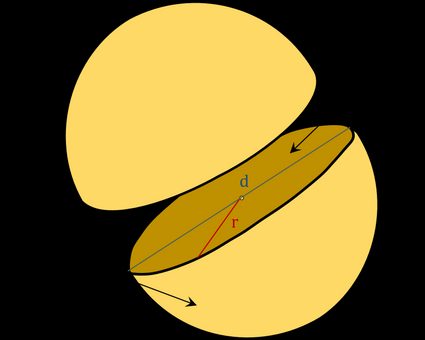
Are you curious about what principles lie behind our tool? In the following text, you will learn more about hemisphere properties and find out which volume of hemisphere formulas we have used. In all cases, you need only one of the below quantities:

• $r$ – Radius of a hemisphere;

• $d$ – Diameter of a hemisphere;

• $V$ – Volume of a hemisphere;

• $A$ – Total surface area of a hemisphere;

• $Ab$ – Base surface area of a hemisphere;

• $Ac$ – Cap surface area of a hemisphere; and

• $A/V$ – Surface to volume ratio of a hemisphere.

As the name suggests, a hemisphere is one part of a sphere that is divided into two equal halves. The total surface area of each hemisphere consists of the base area (a circle) and cap area. On the one hand, the sum of two hemispheres' surface areas is not the same as the full sphere surface area, but on the other hand, the sum of two hemispheres' volumes equals the volume of a complete sphere.

If you have already finished calculations related to the hemisphere, you might be interested in our sphere calc to analyze the full sphere.

The simplest way to estimate the volume of a hemisphere is to imagine it as a part of a full sphere. You can find the sphere volume equation in our sphere volume calculator. It is expressed in terms of the radius:

Therefore, the volume of a hemisphere formula is as follows:

The situation is a little more complicated with the surface area. If you want to determine the differences between sphere and hemisphere areas, head to the area of a hemisphere calculator. Briefly speaking, the hemisphere has an additional base area, which you should take into account.

With our volume of a hemisphere calculator, you can perform calculations in many different units (including SI and imperial units). Don't hesitate and check out our volume conversion tool to learn more about various unit conversions!

How to find the volume of a hemisphere when we don't have a radius given? It depends on what you know about a specific hemisphere. Our volume of a hemisphere calculator can calculate, from one chosen parameter, all the other hemisphere quantities. To explain that, let's start by listing some basic equations that describe the properties of a hemisphere:

1. Diameter of a hemisphere: $d = 2r$.

2. Volume of a hemisphere: $V = \frac{2}{3} \pi r^3$.

3. Base surface area of a hemisphere: $Ab = \pi r^2$.

4. Cap surface area of a hemisphere: $Ac = 2 \pi r^2$.

5. Total surface area of a hemisphere: $A = 3 \pi r^2$.

6. Surface to volume ratio of a hemisphere: $A / V = 9 / (2 r)$.

After some simple algebraic transformations, with the above equations, we can finally write six explicit volume of hemisphere formulas that are used by our volume of a hemisphere calculator:

1. Given radius: $V = \frac{2}{3} \pi r^3$.

2. Given diameter: $V = \frac{1}{12} \pi d^3$.

3. Given base area: $V = \frac{2}{3} \sqrt{Ab^3 / \pi}$.

4. Given cap area: $V = \frac{1}{3} \sqrt{Ac^3 / 2 π}$.

5. Given total area: $V = \frac{2}{9} \sqrt{A³ / 3 \pi}$.

6. Given surface to volume ratio: $V = 243 \pi / 4 (A/V)^3$.

You can find hemispheres in many aspects of our life. Many of the surrounding objects are shaped like half of a sphere. In geography and physics, we often say that the Earth is divided into hemispheres: northern and southern. Did you know that when you travel by airplane, "an invisible" force acts on you, taking you off the course? That effect is called the Coriolis effect, and it behaves differently on the northern and southern hemispheres of the Earth. Visit the Coriolis effect calculator to learn more about it!