Last updated: Jun 19, 2024

Tetrahedron Volume Calculator

New

Table of contents

What is a tetrahedron? – Volume, surface area, and height of tetrahedron Spheres of a tetrahedron How to use tetrahedron volume calculator?Example: Using the tetrahedron volume calculator Using tetrahedrons FAQs

The tetrahedron volume calculator determines the volume and surface area of a tetrahedron. In addition to this, the calculator will also help you find other properties such as the height of tetrahedron, surface area to volume ratio, sizes of various spheres like insphere, midsphere, and circumsphere. Read on to understand the properties of a tetrahedron, how to use volume of a tetrahedron formula along with various spheres and how to calculate surface area to volume ratio.

If you're not interested in the surface area or volume of other shapes, check out our surface area calculator and volume calculator.

What is a tetrahedron? – Volume, surface area, and height of tetrahedron

A tetrahedron is a 3D shape that is formed by joining together 4 triangular faces. It has 4 vertices, 6 edges, and 4 faces. We can see different views of a tetrahedron in the figure below, with labels for height H and edge length L. This shape is otherwise known as a triangular pyramid, i.e., a pyramid with a triangular base.

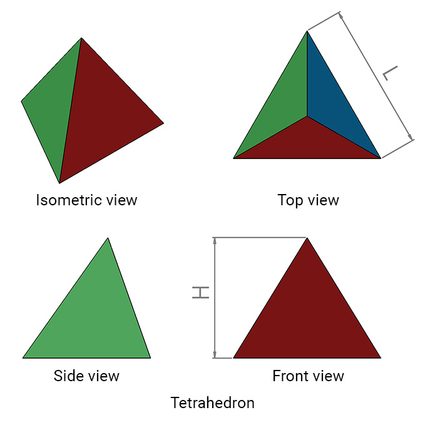
The height H of a tetrahedron is related to its edge length L can be written as:

H = \frac{\sqrt{6}}{3} L

The volume of tetrahedron formula can be written as:

V = \frac{L^3}{6\sqrt 2}

Similarly, the area of a tetrahedron A can be determined from the equation:

A = \sqrt 3 L^2

You can observe that the surface area of the tetrahedron is the product of the number of faces and area of 1 triangular face. You can use the volume and surface area of the tetrahedron to estimate the surface area to volume ratio SVR for this shape.

\frac{\text{Surface Area}} {\text{Volume}} = \frac{\sqrt 3 L^2}{\frac{L^3 }{6\sqrt 2}} = \frac{6 \sqrt 6}{L}

Spheres of a tetrahedron

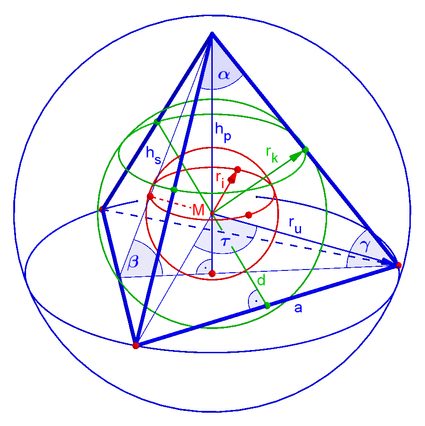
Now that you know how to calculate volume and surface area, let us take a look at different spheres which can be accommodated inside and around a tetrahedron. There are three different kinds of spheres:

Insphere – If you draw a sphere inside the tetrahedron which is tangent to every face of the cell, the sphere is known as an insphere. The calculator will estimate the largest possible size of the sphere that can be contained inside the faces of a tetrahedron with radius $r_\mathrm{i}$ . The insphere is marked in red in the figure below.

\qquad r_\mathrm{i} = \frac{L}{24}

Midsphere – If you draw a sphere which is tangent to every edge of a tetrahedron, the sphere is called a midsphere. In other words, the sphere must touch every edge only at one point. The calculator will return the size of the midsphere having radius $r_\mathrm{k}$ . The midsphere is marked in green in the figure below.

\qquad r_\mathrm{k} = \frac{L}{\sqrt 8}

Circumsphere – The sphere which touches the vertex of the tetrahedron is known as a circumsphere. The calculator determines the size of the circumsphere having radius $r_\mathrm{u}$ . The circumsphere is marked in blue in the figure below.

\qquad r_\mathrm{u} = \frac{L \sqrt 6}{4}

Spheres in and around tetrahedron — Spheres of a tetrahedron (Petrus3743, CC BY-SA 4.0, via Wikimedia Commons).

How to use tetrahedron volume calculator?

Follow the steps below to determine the various properties of your tetrahedron. As you can observe, the properties of a tetrahedron, like surface area, volume, height, etc., are a function of only one variable, i.e., edge length, L. It is fairly easy to operate the tetrahedron volume calculator.

Step 1: Enter the edge length L.
Step 2a: The calculator will provide the height of the tetrahedron.
Step 2b: The volume and surface area of the tetrahedron are also visible.
Step 2c: The volume and surface area used to estimate the surface area to volume ratio.
Step 2d: The sizes of insphere, midsphere, and circumsphere are also determined.

Example: Using the tetrahedron volume calculator

Use the volume of tetrahedron formula to estimate the volume for the cell having edge length L = 80 cm. Also, find the sizes of insphere, midsphere, and circumsphere.

Step 0: Set the units for edge length to cm.
Step 1: Enter the edge length as 80 cm.
Step 2a: The calculator will now return the volume:
Using the volume of tetrahedron formula,

\qquad V = \frac{80^3}{6\sqrt 2} = 0.06034~\mathrm{m^3}

Step 2b: The sizes for the sphere are calculated as:

Insphere:

\qquad r_\mathrm{i} = \frac{80}{24} = 0.1633~\mathrm{m}

Midsphere:

\qquad r_\mathrm{k} = \frac{80}{\sqrt 8} = 0.28284~\mathrm{m}

Circumsphere:

\qquad r_\mathrm{u} = \frac{80 \sqrt 6}{4} = 0.4899~\mathrm{m}

Using tetrahedrons

Did you know:

Tetrahedrons are used in complex stress and deformation-based computer simulations. Large shapes are segmented into smaller elements of tetrahedron shape.
Tetrahedrons are also an observed shape of hybrid or bonded molecules in chemistry.
Some of the ancient civilizations used tetrahedral dices for their board games. So does several current board games.

FAQs

What is a tetrahedron?

A tetrahedron is a 3D pyramidal shape with a triangular base.

How do I calculate the volume of a tetrahedron?

The volume of a tetrahedron formula can be calculated using the edge length, L as:
V = L³ / (6 × √2)

How do I find the height of a tetrahedron?

The height of a tetrahedron can be calculated using the edge length, L as:
H = (√6 / 3) × L

How many faces does a tetrahedron have?

A tetrahedron has 4 faces, 6 edges, and 4 vertices.

How many edges does a tetrahedron have?

A tetrahedron has 6 edges and 4 vertices.

How many vertices does a tetrahedron have?

A tetrahedron has 4 vertices.