Subtraction Calculator

Welcome to Omni's subtraction calculator, where we'll tackle just what the name suggests: subtraction problems.

In essence, the operation is the inverse of addition, but the properties of subtraction are quite different. We'll begin with some theory: the meaning of a difference in math, as well as the formal subtraction math definition.

Obviously, we'll support it all with examples, including instructions on how to subtract numbers in some special cases of the minuend and subtrahend: decimals, negative numbers, etc.

Subtraction is the opposite of addition. To be precise, if we have a sum:

then subtraction turns it around into:

In other words, instead of adding things to a pile, we'll steal some away. The formal yet basic subtraction math definition would be the following:

As a formula, we can write the terms mentioned above as:

(observe that it's also at the top of Omni's subtraction calculator). In other words, the meaning of a difference in math is "whatever we have left after taking the subtrahend away from the minuend."

Next, let's take a look at the properties of subtraction. The thing may be similar to addition, but the rules that govern it are quite different.

Recall that addition (just like multiplication, as you can learn at our multiplication calculator) is commutative. In other words, the $a$ and $b$ can exchange places in the first formula from the above section, and the result will stay the same.

On the other hand, subtraction (just like division) is not commutative. Therefore, the minuend is always the first of the numbers, while the second is the subtrahend (that's also why they have different names). For instance, $c - a$ is something different from $a - c$.

Switching places of the numbers is one thing, but what about switching the place of the operator? Try it with our Polish notation converter!

However, if you've studied general integers, you know that negative numbers exist. And if we know that much, we can use it to explain the connection between addition and subtraction even better.

At the top of the above section, we said that subtraction is the opposite of addition. Formally, this means that subtracting a value is the same as adding its opposite, i.e., the number with the opposite sign. For instance:

And:

And once we have a sum, we can use tricks such as commutativity or the distributive property (if you don't remember the latter, visit Omni's distributive property calculator for a refresh). However, we have to be careful to keep track of the signs.

We've seen the subtraction math definition, the properties and even began to see actual numbers. It's high time we finally explain how to subtract in practice.

Subtraction problems (the basic ones, at least) ask how much we'll have left once we give away, sell, eat, etc., some of what we had initially. For instance, if we have $5$ donuts and decide to eat $2$ for lunch, we'll end up with $5 - 2 = 3$ left and too much sugar in our blood.

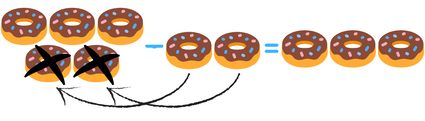
Still, there's more to math than just that and more to Omni's subtraction calculator than just a subtracting integers calculator.

For decimals, the operation works similarly. In essence, it all boils down to considering integers, but we have to keep track of the decimal dot. To make it more precise, we need the minuend and subtrahend to have the same number of digits after (i.e., to the right of) the dot. If they don't, we recall that decimals are fractions, and therefore, the simplifying rules we met at the simplify fractions calculator apply. In our case, this means that we can write as many zeros at the end of a decimal as we want:

So, when subtracting decimals, we:

1. Make sure they have the same number of digits after the dot;
2. Subtract them as if there was no dot (i.e., as integers); and
3. Place the dot in the result as many digits from the right as it was in the minuend and subtrahend.

For example:

And:

Lastly, we'll cover negative numbers. In fact, we've already touched upon the topic at the end of the above section, but let's describe it all in-depth once more.

In essence, subtracting a positive integer means moving that many places to the left on the number line. For instance, $3 - 2$ means going two steps from $3$ to the left and arriving at $1$. The same works for subtracting a positive number from a negative one. For example:

And:

On the other hand, subtracting negative numbers works a bit differently. The basic rule here is: two minuses give a plus. More formally, following the information at the end of the above section, subtracting a number (positive or negative) is the same as adding its opposite. Therefore:

And:

And:

Note how the last example combines the rules for subtracting negative numbers with those for subtracting decimals. Obviously, our tool serves as more than just a subtracting integers calculator, so it can deal with all such fancy subtraction problems.

As the final touch, let us provide you with a nice step-by-step instructions on how to use the subtraction calculator.

At the top of our tool, you can see the subtraction formula with the names of its consecutive parts, which we use in the subtraction calculator below. For instance, if you'd like to see what is $15$ minus $6$, you need to:

1. Input $15$ into the "Minuend" variable field.
2. Input $6$ into the "Subtrahend" variable field.
3. Read off the result from the "Difference" field.
4. Enjoy the solution and tell all your friends about it.

Remember that subtraction is just one of the four basic arithmetic operations. And, believe it or not, mathematics doesn't end there!

To subtract decimals, you need to:

1. Check if they have the same number of digits after the dot.
2. If they don't, add zeros to the short one accordingly.
3. Subtract the numbers as if there was no dot.
4. Place the dot as many digits from the right as it was initially.
5. Enjoy your result of subtracting decimals.

To subtract integers, you need to:

1. Write the subtrahend under the minuend.

2. Subtract the leftmost bottom digit from the top one.

3. If the top one is too small:

   • Subtract 1 from the next top one;

   • Add 10 to the "too small" digit; and

   • Subtract the bottom digit as in step 2.

4. Repeat for consecutive digits.

5. Enjoy your result of subtracting integers.

To subtract negative numbers, say, a from b, you need to:

1. Look for a on the negative and positive number line.
2. Moveb positions from a:
   • To the right, if b is positive; or
   • To the left, if b is negative.
3. The point you end up in is the difference.
4. Enjoy your result of subtracting negative numbers.

Yes. By definition, the result of subtracting two numbers is called their difference.

No. As opposed to, for example, addition, subtraction is not a commutative operation. Indeed, for instance,10 - 3 = 7 but 3 - 10 = -7.

To subtract a negative number from a positive number, you need to:

1. Switch the negative number to its positive equivalent.
2. Change subtraction into addition (e.g., 10 - (-3) = 10 + 3).
3. Add the two positive numbers.
4. Enjoy your result of subtracting the numbers.

No. As opposed to, for example, addition, subtraction is not an associative operation. Indeed, for instance, 10 - (3 - 1) = 10 - 2 = 8, while >(10 - 3) - 1 = 7 - 1 = 6.

No. By definition, natural numbers are positive integers (i.e., whole numbers) and, for instance, 2 - 6 = -4, which is a negative integer but not a natural number.

Addition and subtraction are inverse operations. In other words, whenever we have a sum a + b = c, the numbers must satisfy similar subtraction relations: c - a = b and c - b = a.

To phrase it differently, subtraction is the same as adding the opposite number. Therefore, instead of subtracting a value, we can add its opposite (i.e., the number with the opposite sign). For example, 2 - 6 = 2 + (-6) = -4 or 10 - (-3) = 10 + 3 = 13.