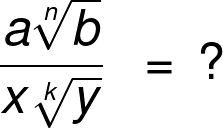Rationalize Denominator Calculator
Welcome to Omni's rationalize denominator calculator, where we'll show you how to get rid of a square root or any other radical from the denominator. In general, roots tend to be irrational, so the procedure is called rationalization in math language. It may sound fancy and difficult, but, in fact, it boils down to applying a few simple rules. To get a firmer grip on the matter, we'll support the theory by showing you how to rationalize the denominator and simplify the resulting expression on a few rationalization examples.
Ready for some cool mathematical magic? Well, here it comes!
Exponents and radicals
Have we ever told you the definition of insanity? It's repeating the same thing over and over again instead of doing it in a faster, simpler way. Like when you have to add the same number several times when you can use multiplication instead.
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 8 * 5
Similarly, when we go one step further and need to multiply by the same value several times, it would be really troublesome to write all the *-s. Again, there's a far easier way - exponents.
5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 = 58
Unfortunately, even though we've successfully avoided insanity, all this talk made mathematicians add some new questions to the pile. Oh, bother...
Whenever we have some mathematical operation, scientists like to have some way to work it backward. In other words, when we look at the result, we'd like to be able to figure out where it came from. For example, if the operation is addition, then we can reverse it using subtraction.
We can easily find the inverse operation for the first of the above - it's division. To be precise, when we look at the 8 * 5 = 40 above and want to find out what it was that we multiplied 8 by, it's enough to find the quotient 40 / 8 = 5.
Radicals (also called roots) are the inverse operation to exponents. For the 58 = 390,625 from before, this means that in order to retrieve the number that we raised to the 8-th power, we need to find the 8-th root: 8√390,625 = 5.
This time, we began the whole thing by finding out that 58 = 390,625. How would we find the answer without that? Or what would be, say, 8√390,624? It certainly isn't 5, but it doesn't look like 4 either.
In general, calculating radicals is difficult. The problem is that such expressions are often irrational, i.e., cannot be written accurately (without rounding) as a fraction. Calculations tend to get rougher and rougher with every such root. Arguably, the worst case is when they appear in the denominator - we then don't even know too well what we have down there. And that's precisely where rationalization in math comes into play.
But what does rationalize mean? Well, we'll have to wait till the next section and see, won't we?
Rationalization in math: how to get rid of a square root
We don't like radicals in the denominator. On the one hand, if we see 2√3, then it's simply two square roots of three, which (for mathematicians, at least) sounds and looks just fine. On the other hand, 2 / √3 is a monstrosity that no self-respecting scientist is satisfied with. Well, let them have their kinks, we say.
The meaning of rationalize is to make those fussy mathematicians happy. Rationalization in math means more precisely to rationalize the denominator of your expression, i.e., to transfer the radicals from the denominator to the numerator. Mind you, the value of the whole thing will most likely stay irrational; it's just that the number under the line will not.
From a theoretical point of view, rationalization in math boils down to multiplying the expression by 1. Yup, by the very number that doesn't change anything in multiplication. However, the trick is to have this 1 written in a way that actually makes a difference. After all,
1 = 2 / 2 = 2020 / 2020 = √13 / √13 = (9 - ³√7) / (9 - ³√7).
In other words, we express 1 as a suitable quotient. Then we use the fact that multiplying fractions translates to numerator times numerator over denominator times denominator.
For instance, say that we have an expression of the form a / √b, and let's see how to get rid of a square root in that case. We can write:
a / √b = (a / √b) * 1 = (a / √b) * (√b / √b).
We chose to write 1 as √b / √b. We can, because... reasons. This gives:
a / √b = (a / √b) * (√b / √b) = (a * √b) / (√b * √b) = (a√b) / b = (a/b) * √b.
In the end, we got an equivalent expression, but the root is no longer in the denominator. To be precise, the meaning of rationalize, in this case, was to transform what we had into a fraction (i.e., a rational number) times the very radical that created the problem in the first place.
"But what if I had a root of higher-order in the denominator? Or what if I had a sum of two square roots instead? What does rationalize mean then, and how does it work?"
Well, it's a good thing you asked because the next section is here to answer both of these questions!
How to rationalize the denominator and simplify the result
Our rationalize denominator calculator deals with four types of dividing radical expressions: radical / radical, sum / radical, radical / sum, and sum / sum. Below we focus on them one by one and describe how math rationalization works in each case. You may also benefit from taking quick look at Omni's dividing radicals calculator.
- radical / radical - (a * n√b) / (x * k√y)
The simplest case we can have. In order to rationalize the denominator and simplify the result, we need to multiply our expression by k√(yk-1) / k√(yk-1). This will give in the denominator x * k√y * k√(yk-1) = x * k√(yk) = x * y. Note that for
k = 2this boils down to knowing how to get rid of a square root, i.e., to what we did in the above section.
- sum / radical - (a * n√b + c * m√d) / (x * k√y)
Similar to point 1., but this time we have two summands in the numerator. Fortunately, this doesn't change the process much since we're concerned only with math rationalization of the denominator, which happens to be the same. In other words, we again multiply by k√(yk-1) / k√(yk-1) and obtain
x * yunderneath as a result. However, be careful to multiply both summands from the numerator by k√(yk-1) and not just one of them.
- radical / sum - (a * √b) / (x * √y + z * √u)
Here's when things get interesting. This time, it's both summands of the denominator that we need to rationalize, meaning that we have to take care of both at the same time. To do this, we use the formula (a - b) * (a + b) = a² - b², which gives us two squares (and nothing else), which kill square roots (note that this formula works only for radicals of order
2). That means that we need to multiply our expression by (x * √y - z * √u) / (x * √y - z * √u) (i.e., the denominator with the opposite side in the middle) to get x² - y² at the bottom. However, remember to multiply the numerators correctly!
- sum / sum - (a * √b + c * √d) / (x * √y + z * √u)
Similar to point 3. in the same way point 2. was to point 1. Again, the extra summand above doesn't change the process: we still multiply the whole thing by (x * √y - z * √u) / (x * √y - z * √u). However, multiplying the radical expressions in the numerators this time gives four summands: each element of the first times each of the second (see the multiplying radicals calculator).
Remember that the meaning of rationalize is to make the expression prettier somehow. In general, it may happen that the thing we get after rationalization in math can still be made simpler. The rules for how to do that are a topic for a whole article, so we refer you to our simplifying radicals calculator to learn all about them. For now, let's just mention that Omni's rationalize denominator calculator not only applies the rules mentioned in the four points above but also simplifies the roots we obtain.
With this, we conclude the part on how to rationalize the denominator and simplify the result. That marks the moment where we're ready to face some rationalization examples that actually have numbers.
Rationalization examples: using the rationalize denominator calculator
Let's take on two expressions and see how to rationalize the denominator and simplify the result in both cases:
³√18 / (2 * √3) and (1 + 2 * √5) / (√10 - 2 * √2).
First, let's feed these rationalization examples to the rationalize denominator calculator to see how easy it makes our lives.
For the first one, we see that the numerator and denominator are single expressions, i.e., there is no sum in either. That means that the example falls under the first option from the calculator: radical / radical. We choose this option under Expression, which triggers a symbolic representation of such a thing at the top of our tool.
We see there (a * n√b) / (x * k√y) and all these letters appear underneath in separate fields. In our case, we input:
b = 18, n = 3, x = 2, y = 3, k = 2.
Note how we have no number in front of the cube root ³√18, so we left a blank (i.e., the symbol representing the number before the radical in the numerator). In fact, this means that a = 1, but the rationalize denominator calculator will understand that even if we leave the field empty. Also, observe how we put k = 2 even though there is no number in the root from the denominator in our expression. That is because by convention, in square roots (i.e., roots of order 2), we don't write the ².
Once we input all the numbers, we can read off the result from underneath. Observe how the rationalize denominator calculator also provides a step-by-step solution to the problem.
Next, let's take on the second expression. We see that there we have a sum in the numerator and a difference in the denominator. Recall that subtracting a number is the same as adding its opposite, so we choose sum / sum under Expression.
A symbolic expression (a * √b + c * √d) / (x * √y + z * √u) appears. We input:
a = 1, b = 1, c = 2, d = 5, y = 10, z = -2, u = 2.
Observe how the first summand above has no radical. Therefore (as suggested in the note under the symbolic expression), we input b = 1 (which kills the root). Also, we left x blank since there is no number in front of √10. Lastly, observe how we wrote z = -2 to have a difference in the denominator.
Again, once we input all the numbers, the answer appears underneath, and again it is accompanied by a step-by-step solution.
However, sometimes we need to do tiresome calculations by hand, so let's see how to rationalize the denominators and simplify the results ourselves.
Firstly, let's see what we can do with ³√18 / (2 * √3). Recall how to get rid of a square root in the second section. In our case, we need to tackle √3, so we write:
3√18 / (2 * √3) = [3√18 / (2 * √3)] * (√3 / √3) = (3√18 * √3) / (2 * √3 * √3) = 6√8748 / 6 = (3 * 6√12) / 6 = 0.5 * 6√12.
Next, we deal with (1 + 2 * √5) / (√10 - 2 * √2). According to the rules in point 4. in the above section, we write
(1 + 2 * √5) / (√10 - 2 * √2) = [(1 + 2 * √5) / (√10 - 2 * √2)] * [(√10 + 2 * √2) / (√10 + 2 * √2)] = [(1 + 2 * √5) * (√10 + 2 * √2)] / [(√10 - 2 * √2) * (√10 + 2 * √2)] = (√10 + 2 * √2 + 2 * √50 + 4 * √10) / (10 - 4 * 2) = (5 * √10 + 12 * √2) / 2 = 2.5 * √10 + 6 * √2.
(To have the radical simplification from the last steps in both calculations in detail, see the above section.)
Phew, that was time-consuming in comparison with how fast the rationalize denominator calculator dealt with the problem, wouldn't you say? Still, we better memorize a thing or two for any surprise math test at school.