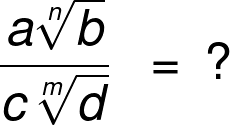Dividing Radicals Calculator

Welcome to Omni's dividing radicals calculator, where we'll learn all about finding the quotient of two roots of arbitrary order. The operation itself is not too tricky; it's enough to remember a few rules and apply them. Nevertheless, we'll start slow by showing you how to divide square roots, but soon move on to see how to divide radicals of arbitrary order.

Let's jump straight to it, shall we?

You know how they say that you learn by repetition? Well, there's some truth to it, to be sure, but sometimes repeating the same thing several times can be mind-numbing and exhausting. And if there's any group that hates their brains going numb, it's mathematicians.

Whenever you have to add the same number, again and again, it may be tiring to write the + signs one after the other. Fortunately, scientists decided that they're too lazy for such menial tasks and invented multiplication.

5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 8 * 5

Well, an obvious question comes to mind, doesn't it? Since they proved so smart, what do they do if they have to multiply the same number several times? And again, mathematicians decided that their time is too valuable to write so many *s. Therefore, they came up with exponents.

5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 = 5⁸

However, it soon proved that these are sometimes not enough. After all, it's not always that we want to add items to the pile; sometimes, we also want to take them away. That's why we need operations that work the other way, similar to how subtraction is the inverse of addition.

For multiplication, it's not too difficult: the inverse operation is division. For example, if we take the 8 * 5 = 40 from above, knowing that we multiplied by 8 to get it, division will return the 5.

40 / 8 = 5

Radicals (also called roots) are the inverses to exponents. That means that in our case, if we take the 5⁸ = 390,625 knowing that we raised a number to the 8-th power to get it, the (8-th) root of that number will give us the 5.

⁸√390,625 = 5

But what if we didn't begin with studying 5⁸ beforehand? How would we guess from the large number 390,625 that its 8-th radical is 5? Or what would the result be if we took, say, 390,624 instead?

Well, truth be told, in general, it's not so easy to calculate radicals. In fact, for more complicated cases, we usually turn to external tools - something like our dividing radicals calculator. Nevertheless, a few tips and tricks may come in handy when faced with such expressions. We'll show you all of them, but we start slow: with how to divide square roots.

The steps we follow when dividing radicals are very similar to those of multiplying radicals. In essence, we begin by taking advantage of the properties of roots and reducing the whole expression into something with only one radical.

In general, dividing square roots starts by rationalizing the denominator:

(a√b) / (c√d) = (a / (c * d)) * √(b * d).

However, this is often not the end. For instance, let's try to divide 5√6 by 2√10. The above formula gives:

(5√30) / (2√10) = (5 / (2 * 10)) * √(30 * 10) = 0.25 * √300.

Although it may seem like the best we can get at first, we can still write it in a much nicer way. To be precise, we'll simplify the radical √300 into a more agreeable number. The basic tool for such things is prime factorization, i.e., we decompose the 300 into a product of prime numbers.

300 = 2 * 2 * 3 * 5 * 5 = 2² * 3 * 5²

Next, since our root is of order 2 (in other words, a square root), we look for pairs of the same prime numbers in the factorization. In our case, we have two such couples: a pair of 2s and a pair of 5s. We pull the numbers representing these pairs out of the radical and keep the rest (the singles) inside. All in all, dividing the square roots gives:

(5√30) / (2√10) = 0.25 * √300 = 0.25 * √(2² * 3 * 5²) = 0.25 * 2 * 5 * √3 = 2.5 * √3.

A prettier number than the one above, don't you think?

"Fair enough, we now know how to divide square roots, but what about more complicated ones? What about cube roots? Or even higher orders?"

Well, we're glad you asked because the next section is there to show you how to divide radicals of arbitrary order. We hope you're ready for it because here it comes!

The good news is that if we know how to divide square roots, then we're good with ninety percent of the process. With higher radicals, we again start by applying a formula, only this time, it's a bit more complicated.

(a * ⁿ√b) / (c * ᵐ√d) = (a / (c * dᵐ⁻¹)) * ᵏ√(bˢ * dᵗ),

where k = lcm(n,m) (the least common multiple), s = k / n, and t = (k * (m - 1)) / m. The extra numbers come from rationalizing the denominator and the properties of radicals.

Also, now that we have a radical of order k (which is not necessarily a square root), we need to look for groups of k same primes in the factorization when we try to simplify the radical. These we can pull out of the root (similarly to how we did in the above section), and the ones that didn't have complete k-tuples stay inside.

Lastly, it may happen that after all these operations, there is yet another thing we could do. To be precise, after we pull out all that we could out of the root, the root itself can sometimes still be simplified further. If all the primes under the radical have powers with a common factor with the root's order, we can reduce them in a similar way we reduce fractions to obtain an equivalent one.

Symbolically, this rule looks like this:

ᵏⁿ√(aᵏˢ * bᵏᵗ * cᵏᵘ * dᵏ*ᵛ * ...) = ⁿ√(aˢ * bᵗ * cᵘ * dᵛ * ...).

For instance:

⁶√(2⁴ * 5¹⁰ * 7²) = ³√(2² * 5⁵ * 7¹).

The good thing is that with our dividing radicals calculator, you don't have to apply any of these properties - the calculator will do all that for you. Oh, what a tool!

There is just one last thing that we'd like to do before we let you off into the world with all this new knowledge. We've learned so much theory, so we have to try it out on some examples, don't you think?

Say that you're in the middle of some challenging exercise from 3D geometry and that the next question is about the ratio of two edges of your solid. Well, the task doesn't seem too bad; after all, "ratio" is just a fancy way of saying "quotient." (You can read more about it in our ratio calculator.) However, the lengths of both edges involve some radicals, as is often the case when there are right angles involved.

All in all, you face the problem of finding the quotient of 3 * ⁴√64 and 2 * √125. Well, it seems like the perfect opportunity to see how to divide radicals using Omni's dividing radicals calculator!

To begin with, note that at the top of our tool, we see a symbolic representation of the expression we're interested in: (a * ⁿ√b) / (c * ᵐ√d). In our case, we need (3 * ⁴√64) / (2 * √125), so we input into the calculator:

a = 3, b = 64, n = 4, c = 2, d = 125, m = 2.

(Note how we didn't really need to input m = 2 since that option is the default. That is because square roots are the most common radicals out there.)

Once we give all the values, we can simply read off the answer from underneath. Also, observe how the dividing radicals calculator gives a step-by-step solution to your problem.

Still, there may come a time in your life when there's no Wi-Fi around, and you desperately need to find the answer to such a problem. For those unfortunate situations, let's see how to divide the radicals by hand.

First of all, note that the roots we're given are of order 4 and 2, and that lcm(4,2) = 4. Therefore, using the formula from the above section, we get

(3 * ⁴√64) / (2 * √125) = (3 / (2 * 125)) * ⁴√(64 * 125²) = 0.012 * ⁴√1,000,000.

However, this is not yet the simplest form we can have. We can simplify the radical we obtained, so we begin by finding the prime factorization of the number under it:

1,000,000 = 2 * 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5 * 5 * 5 = 2⁶ * 5⁶.

Next, since we have a root of order 4, we look for groups of the same four primes in the factorization. Here, we have two: four 2s and four 5s, which leaves two 2s and two 5s alone. We pull the numbers representing full groups out of the radical and keep the rest inside:

(3 * ⁴√64) / (2 * √125) = 0.012 * ⁴√1,000,000 = 0.012 * ⁴√(2⁶ * 5⁶) = 0.012 * 2 * 5 * ⁴√(2² * 5²) = 0.12 * ⁴√(2² * 5²).

Observe how we didn't multiply the numbers under the root. That is because we can simplify the expression further since the radical's order and the powers of all primes inside have a common factor (i.e., 2). Therefore, we can reduce the order with the exponents and obtain:

(3 * ⁴√64) / (2 * √125) = 0.12 * ⁴√(2² * 5²) = 0.12 * √(2 * 5) = 0.12 * √10.

A much prettier expression, wouldn't you say?