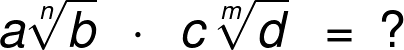Multiplying Radicals Calculator

Welcome to Omni's multiplying radicals calculator, where we'll take two expressions that contain roots and find their product. The operation itself is not too difficult and it's enough to remember a few rules. We begin with square root multiplication and, based on that, show how to multiply radicals in general.

Let's not waste a second longer. Multiplying roots, here we come!

In general, people tend to be lazy. And with mathematicians, it's twice as bad.

When some smart scientist had to add the same number several times, he decided he'd have none of that and invented multiplication to write the same extended expressions a lot faster.

Then, a generation or two later, their successors faced a very similar problem: multiplication by the same number several times. At that moment, they recalled the wit of their ancestor and proudly said that they wouldn't have any of that either. And this, dear kids, is how exponents were born.

Unfortunately for the sleepy students of today (but fortunately for science), both times there came some other guy who arrived a bit late to the party and heard only the last few words. Confused, they asked if they could somehow get the number we started with from the end result, i.e., if they could invert the process. And that's the story of how when you arrive late, you end up inventing inverse functions.

In the first case, the inverse of multiplication is division. That means that given $40$ and knowing that you multiplied something by $8$, you need to divide the $40$ to obtain that something.

Radicals (also called roots) are the inverses to exponents. In our example, when we get the number $390,625$ and know that it's something to the eighth power, the (8^th) root of that $390,625$ will return the $5$.

This time, it was quite simple to know that $\sqrt[8]{390,625} = 5$ because we began by looking at $5^8$. But suppose that we didn't. How would we find the answer then? Or, e.g., what would $\sqrt[8]{390,625}$ be? Clearly, it can't be $4$ or $5$.

In fact, it's not so easy to compute roots in general. Usually, we turn to external tools for help in more complicated cases, like our multiplying radical expressions calculator. Nevertheless, there are a few tricks and properties that can save the day, and we'll try them out by showing you how to multiply square roots.

We'll explain multiplying square roots by looking at the expression $a\sqrt b \times c\sqrt d$ (note that an analogous equation is at the top of the multiplying radicals calculator). The basic rule is very simple: numbers outside of the roots and those inside belong separately. To be precise, the following identity holds true:

To some extent, this is all there is to multiplying square roots. However, the answer we get this way is often not satisfactory, i.e.; it may be possible to simplify the resulting radical expression.

For instance, take $3\sqrt{30} \times 5\sqrt {6}$. By the above, we have:

Before we rush to say that this is our final answer, let's take a closer look at the radical. Multiplying the roots made the number something that we can write in a nicer way. To be precise, we're going to simplify the radical expression: we teach you how to do it with our simplifying radicals calculator.

To do this, we begin by finding the prime factorization (if you don't remember how to do it, we've got your back: try our prime factorization calculator) of the number under the root:

Among the above primes, we look for pairs of the same ones. In our case, we have two: a couple of $2$s and a couple of $3$s. We pull the numbers representing each couple out of the radical and keep the ones that didn't find a pair under it.

Only now we can safely say that we've finished the square root multiplication and that we've arrived at the simplest radical form. Note that Omni's multiplying radical expressions calculator provides a similar step-by-step solution.

"But what if instead of multiplying square roots, we had radicals of a higher order? Are the calculations any different then?" Well, how fortunate of you to ask! Allow us to invite you to the next section to find the answers to those questions.

In short, once we know how to multiply square roots, we know how to multiply any radicals. There is just a couple of small changes to the procedure presented in the above section.

First of all, when we're multiplying roots of the form $a \times\sqrt[n]{b}\times c\times\sqrt[m]{d}$, the formula we begin with is as follows:

where $k = \text{lcm}(n,m)$ (the least common multiple), $s = k / n$, and $t = k / m$. The identity is a straightforward consequence of the properties of radicals.

Secondly, remember that now the resulting root is of order $k$ and not $2$ (recall that by convention, for square roots, we don't write the small $^2$ next to the root symbol). That means that if we want to simplify the radical expression, we need to look for groups of the same $k$ primes in the factorization (instead of pairs).

Additionally, now that we have radicals of higher-order, there may be one more thing we could do. To be precise, after we pull out all that we could out of the root, the root itself can sometimes still be simplified further. If all the primes under the radical have powers with a common factor with the root's order, we can reduce them in a similar way we calculate the equivalent fractions.

Symbolically, this rule looks like this:

For instance:

All in all, it's not too bad, is it? So now that we know how to multiply radicals, why don't we try our luck with a cool numerical example?

Say that your little brother has just learned about multiplication at school and is all too eager to catch you out with some exercise you won't be able to do. After you've gone through $2\times2$ and even $7\times8$, the young one starts to get creative. He runs to the bookshelf, grabs your math coursebook, and points at two random expressions he finds. He may not understand what the flimsy $\sqrt{\ }$ stands for, but there are some numbers next to it, so it should do.

Not naming the values, your brother asks you to multiply $2 \times\sqrt[3]{12}$ and $5 \times\sqrt{6}$. Oh, what a coincidence! That seems like just the task for our multiplying radicals calculator! We can't show weakness in front of the little one, can we?

At the top of our tool, we see a symbolic representation of multiplying roots: $a \times \sqrt[n]{b}\times c \times \sqrt[m]{d}$. Since we want to find $2 \times\sqrt[3]{12}\times 5 \times\sqrt{18}$, we need to input:

For the first factor, and:

For the second one. Once we give the last value, we can simply read off the result from underneath. Observe how the multiplying radical expressions calculator also gives a step-by-step solution.

Well, Omni sure saved us a lot of time (and time is money, after all), but how about we impress our little brother some more? Let's see how to multiply the radicals by hand.

First of all, we note that the roots we're dealing with are of order $3$ (also called a cube root) and $2$ and that $\text{lcm}(3,2) = 6$. Therefore, using the formula from the above section, we get

Next, we need to simplify the radical that we got. To do that, we begin by finding the prime factorization of the number under it:

Now we look for groups of six same primes in the factorization. In our case, we have two: six $2$s and six $3$s, which leaves one $2$ and two $3$s alone. We pull the numbers representing the full groups out of the radical and leave the rest under it. That gives:

Wonderful, we've arrived at our final answer! Surely, our little brother will look at us in awe for that for weeks. Still, we better prepare a little for when he comes back after learning how to calculate division.