Perimeter of a Sector Calculator

The perimeter of a sector calculator is a tool made to rescue you from problems faced in geometry. Yes, a sector of a circle could become a headscratcher but not when you have Omni on your side! Here we are to discuss many aspects of the perimeter of a circle sector:

• What is the perimeter of a sector?
• What is the formula for the perimeter of a sector?
• How to calculate the perimeter of a sector?

The perimeter of a sector calculator is a tool made to make your life, at least the mathematical aspect of it, easy and convenient. Needless to say, using our calculator is a piece of cake. In fact, a slice of cake is just the right example to visualize the sector of a circle. Fascinating, isn't it?

The steps to use our tool are:

1. Enter the central angle of the sector. You have an option to choose between units like degrees and radians.
2. Enter the radius of the circle. You again have a list of options to choose the unit. The centimeter is the default unit.
3. The tool will estimate the arc length and then use it to swiftly give you the perimeter of the sector.

For instance, you enter 2 radians as the central angle and 7 cm as the radius. The result is 28 cm, the perimeter of the sector.

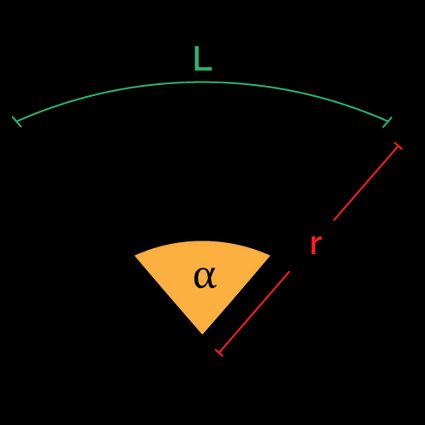
The perimeter of a sector is the measure of the boundary of a section of a circle, which is why it is called a sector. The formula uses the sector's radius $r$ and arc length $L$ to determine the sector's perimeter $P$ under consideration:

$P = 2 \times r\ +\ L$

This perimeter of a sector formula is simple, but it assumes you know the arc length. In fact, the arc length is not that easy to measure directly, and it is better to calculate it using the central angle $\alpha$:

$L = \alpha \times r$

Plugging this formula for $L$ into our initial formula for $P$, we arrive at the following perimeter formula:

$P = 2\times r \ + \ \alpha \times r$

where:

• $P$ - The perimeter of the sector;
• $\alpha$ - The central angle;
• $r$ - The radius; and
• $L$ - The arc length.

No amount of knowledge can be thought of as being enough! That's why we keep adding more tools to our collection for you.

Once you're done with finding the perimeter of sectors, take a look at some other Omni tools related to a circle's sector.

• Sector area calculator;
• Quarter circle calculator;
• Quarter circle area calculator; and
• Quarter circle perimeter calculator.

Finding the perimeter of a sector is easy! Use the formula:

Perimeter = (2 × radius) + arc length

All you have to do is:

1. Multiply the radius by two, which gives the circle's diameter.
2. Add the result from Step 1 to the arc length of the sector.
3. The result is the perimeter of the sector of the circle.

The perimeter in itself is the outer boundary of any shape.

So, the perimeter of a circle is the boundary or complete arc of a circle. While the perimeter of a sector is the distance around a particular section of a circle, it includes the two radii and the arc between the radii.

The perimeter of this sector is 28.21 cm.

The formula for the perimeter of a sector is:

Perimeter = (2 × radius) + arc length

Here, the arc length equals 10.21 cm. Placing the values in the formula, we have:

Perimeter = 2 × 9 + 10.21

Perimeter = 18 + 10.21

Perimeter = 28.21 cm