Lagrange Error Bound Calculator

The Lagrange error bound calculator will help you determine the Lagrange error bound, the largest possible error arising from using the Taylor series to approximate a function. And what's more, this article will show you:

• What the Lagrange error bound is;
• How it relates to the Taylor remainder theorem;
• The Lagrange error bound formula; and
• A worked-out example of how to calculate the Lagrange error bound.

The Lagrange error bound calculator is easy to use! Simply enter your Taylor series problem's values into their corresponding fields:

1. Enter the number of terms from the Taylor series (also known as the resulting Taylor polynomial's degree) into n.
2. Enter the $x$-value at which you're evaluating the error, into x.
3. Enter the polynomial's center in the field labelled a.
4. Enter the maximum value of the $(n+1)$-th derivative of the function you're approximating, $f(x)$, into the field labelled M.

The Lagrange error bound, $e_\text{max}$, will be presented at the bottom of the calculator.

Now, if you find yourself asking questions such as "What is the Taylor series?" or "What is the Lagrange error bound?", then read on!

The Lagrange error bound is the upper bound on the error that results from approximating a function using the Taylor series. Using more terms from the series reduces the error, but it's rarely zero, and it's hard to calculate directly. The error bound tells us what the largest possible error is. The Lagrange error bound formula is derived from the Taylor remainder theorem.

If we have some function $f$, then we can perfectly replicate it using an infinite sum of terms, each expressed using a higher-order derivative of $f$. This endless sum is called the Taylor series.

Let's clarify the above with a mathematical definition — any function $f$ can be replicated by this infinitely long summation:

where:

• $f^{(n)}$ is the $n$-th derivative of the function $f$; and
• $a$ is any point of our choosing, as long as $f(x)$ is infinitely differentiable at $a$.

Below, you can see the Taylor series in action, as it approximates $f(x) = e^x$ with more and more terms, i.e., as the value of $n$ becomes higher and higher:

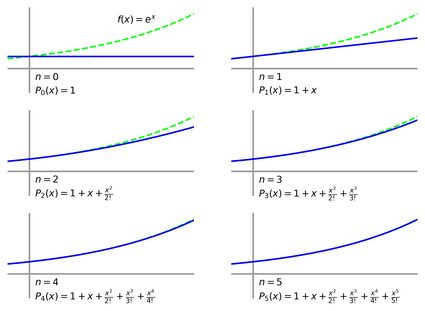
Isn't that amazing? With only a 5th-degree polynomial, we can already approximate $e^x$ to a high degree of accuracy.

However, we now see a problem: the Taylor series' definition is only true if we use an infinite number of terms. If we stop anywhere short of infinity — and as mortals, we must — then we'd only have approximated $f(x)$ with the Taylor polynomial, $P_n(x)$:

Because $P_n(x)$ is just an approximation of $f(x)$, there will be a remainder, $R_n(x)$:

What is the value of $R_n(x)$? We can't know for sure because there are countless terms to calculate. We do know that the more terms we include from the series (i.e., the higher the polynomial's degree, $n$), the better we approximate $f(x)$ with $P_n(x)$, and the smaller that error will become.

Lucky for us, there is an upper bound on $R_n(x)$, a worst-case-scenario estimate of the error. It's called the Lagrange error bound, and this calculator and text is all about finding it.

The Lagrange error bound formula is as follows:

where:

• $e_\text{max}$ — Lagrange error bound;
• $x$ — Where we're determining the error between $f(x)$ and $P_n(x)$;
• $a$ — Where the polynomial is centered;
• $n$ — Number of terms from the Taylor series we're including, and thus the degree of the resulting polynomial; and
• $M$ — Largest value of $\left\vert f^{(n+1)}(z) \right\vert$ for all $z$ between $a$ and $x$:

Using $e_\text{max}$, we can place a bound on $R_n$:

which simply states that $R_n(x)$ cannot be larger in magnitude than $e_\text{max}$, thereby providing an upper bound on any error that might result from the approximation of $f(x)$.

That's enough formulae — let's look at an example of the Lagrange error bound and how it's calculated.

Let's find the error bound for the function $\sin(x)$ at $\pi/3$ when approximated by a 4th-order Taylor polynomial centered around $\pi/6$.

Right off the bat, we have some values ready to be plugged into our Lagrange error bound formula:

• $f(x) = \sin(x)$;
• $x = \pi/3$;
• $n = 4$; and
• $a = \pi/6$.

The hardest part will be determining $M$, the largest value of the $(n+1) = 5$th differential of $f(x)$ within our interval $[a, x] = [\pi/6, \pi/3]$. Let's find it.

The higher-order differentials of $\sin(x)$ are given below:

Great! $f^{(5)}(x) = \cos(x)$. Now we need to know what the biggest value of $\cos(x)$ can be at any point in the range $[\pi/6, \pi/3]$. We could use some fancy mathematics for this, but we can also reason that

• $\cos(0) = 1$;
• $\cos(\pi/2) = 0$; and
• $\cos(x)$ is strictly descending over the range $0 \le x \le \pi/2$.

So, the largest value of $\cos(x)$ in our range of $[\pi/6, \pi/3]$ should be closer to $x=0$, and therefore $M = \cos(\pi/6)$.

Now, we have everything we need to determine $e_\text{max}$:

Thanks to this result, we know that our error cannot be greater than 0.000284. Let's see if that's true:

The Lagrange error bound is correct! And what's more, if we took the same steps for other values of $n$, we can see how the error bound decreases as we approximate $f(x)$ better:

And there you have it. We've shown you how to calculate the Lagrange error bound — now it's your turn!