Pizza Comparison Calculator (old version)
Check out the pizza size calculator!, the newer version of the pizza comparison calculator 🍕
How often have you wondered whether it's better to get 2 medium pizzas or just 1 large pizza? Or ended up searching for "pizza comparison", hoping to make the right choice to satisfy your cravings? Probably quite a few. Pizzerias usually tell you the pizza pie's diameter, but we don't eat the diameter. We don't eat the circumference either. What we eat is the area of the pizza. It's very basic maths that revolves around the equation Area = Radius² × π, but we're often in too much of a hurry or just can't be bothered to calculate it in our heads. That's why we built this comparison calculator for pizza sizes: to solve these problems once and for all. Keep reading to learn the math behind pizzas and to visualize the different growths of circumference and area in an effective 12-inch pizza size comparison. Keep reading to learn:
- How to perform a mathematically correct pizza comparison;
- Why do we use a 12-inch pizza in the size comparison; and
- How to use our pizza size comparison calculator.
The geometry of a pizza
What's the geometry of a pizza? It all lies in circles. A circle is a basic shape, arguably the simplest or most complex you can imagine. Composed of an infinite number of sides arranged at a constant distance from a central point, circles require some particular formulas to compute their perimeters or area. Both these formulas make use of pi or π.
Starting from this, we can find the formula for the circumference of a circle (its perimeter):
Where is the diameter. This is the way is most often defined: invert the formula, and you'll find it as the ratio between a circle's perimeter and its diameter.
In terms of pizzas, this is the length of the crust (of its outer rim). We are not interested in this quantity for now, as the deliciousness of the pizza lies inside the crust! To compute this quantity, we need to learn how to calculate the area of a circle.
To do so, we use the following formula:
The first thing we notice is that we don't use the diameter anymore, but the radius. You can see why in the following illustration.
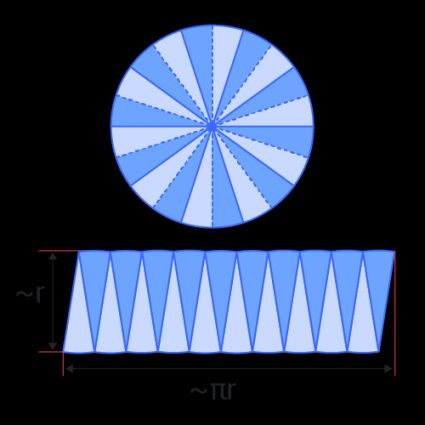
Regardless of the illustration, you can already see a fundamental difference in the formula: the length (the diameter in the circumference and the radius in the area) scales with a different exponent.
A problem of scaling
What are the consequences of a different exponent when calculating perimeter and area? Though it's not straightforward to compare a length (the circumference) and a surface (the area), we can see how the behaviors differ by using a simple comparison.
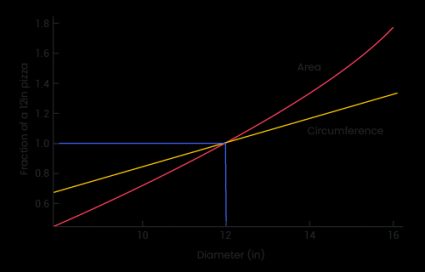
This graph plots the growth of the circumference and the area of a pizza as a function of the growing diameter. To allow you to compare a length (the diameter, with units in) and a surface (the area, with units in2), we scaled these quantities using as a reference an average 12-inch pizza. This allows us to identify three regions of this graph:
- For a diameter of 12 inches, the pizza's circumference and area correspond to the reference. Hence we are at the intersection of the curve.
- For diameters smaller than 12 inches, the circumference is larger than the area if we compare them to the reference. This means that for a pizza smaller than 12 inches, you'd get relatively more crust than toppings!
- For diameters greater than 12 inches, the area starts growing much faster than the circumference. Compared to the reference, larger pizzas have much more filling than smaller ones.
🙋 Notice how these calculations use a reference value. The effective increase in topping and crust is not directly comparable! Think about it: these are very different things, and using them in a pizza comparison makes no sense.
It's worth saying that opting for a larger pizza is almost always more cost-effective. As is the case in any other industry, pizzerias have better margins/markups on smaller products. The table below shows how quickly a pizza's area grows as the pizza diameter increases. As a result, an 18-inch pizza is over three times larger than a 10-inch one. At the same time, grabbing a monster 61-centimeter pizza will feed more people than two 40-centimeter ones or nearly six 25-cm pies.
Diameter [in] | Area [in2] | Diameter [cm] | Area [cm2] | Times bigger than 10in |
|---|---|---|---|---|
10 | 79 | 25.4 | 507 | 1 |
12 | 113 | 30.5 | 730 | 1.4 |
14 | 154 | 35.6 | 993 | 2.0 |
16 | 201 | 40.6 | 1297 | 2.6 |
18 | 254 | 45.7 | 1642 | 3.2 |
20 | 314 | 50.8 | 2027 | 4.0 |
22 | 380 | 55.9 | 2452 | 4.8 |
24 | 452 | 61 | 2919 | 5.8 |
Make sure you use our calculator the next time you order a pizza. You'll be grateful you did the maths once your order arrives. Now it's not only discounts that can save you money!
💡 Got a coupon for your pizza? Then visit the discount calculator to determine how much you'll save on your purchase quickly.
How to use the comparison calculator for pizza sizes
The pizza comparison calculator requires minimal effort from you. Simply type in the diameter, price, and number of smaller pizzas and repeat it for the larger pizza(s) you're considering. This tool will show you the total area and price of each pizza and how they compare to each other, expressed as a percentage. If you only want to compare the areas, skip the prices - this tool will work either way. Units will be defaulted to your country's units but feel free to switch between metric and imperial as you wish, or maybe you could grab 3000 millimeters worth of pizza!
FAQs
Should I order 3 medium or 2 large pizzas?
The size of the pizza is its diameter, and the area of a pizza increases as we increase the diameter. It is almost always a more cost-effective option to choose a large pizza because you get more area, which means more pizza to eat.
Suppose a medium pizza is 12 inches and a large is 16 inches. In that case, Omni's pizza comparison calculator states that the areas for three medium and two large pizzas are 339.29 in² and 402.12 in², respectively. This means you get more with two large pizzas.
Is area of a pizza different from the size I ordered?
Yes, the area and size of a pizza are different properties. We order pizza by its size, which is its diameter. But we do not eat the diameter of the pizza, do we? We eat the area of the pizza.
The formula to calculate the area of a circular pizza is:
area = radius² × pi
Radius is simply diameter divided by 2.
Let's suppose your pizza size is 16 cm. The radius is 8.
So, 8 squared is 64. Multiply this by pi, 3.1416, to get 201.06 cm².
How do I calculate the actual size of a pizza?
To calculate the size (area) of a circular pizza, follow these simple steps:
- Find or measure the radius of the pizza, r.
- Calculate the square of the radius, r².
- Multiply the result by π.
Let's suppose your pizza size is 20 inches in diameter. The radius would be 10 inches.
So, 10 squared is 100. Multiplied by pi, 3.1416, your result is 314.16 in², which is the actual size (area) of the 20-inch pizza you eat.
Does the area of the pizza matter while ordering?
The area of the pizza matters because that is the part that we actually eat. Therefore, don't focus too much on the pizza's diameter or circumference.
The area increases significantly as the diameter changes. However, pizzerias often use diameter to confuse this fact. For instance, the area of a small 8-inch pizza is 50.27 in².