Calculadora de área superficial

Esta calculadora de área superficial te ayuda a encontrar el área de los sólidos tridimensionales más comunes. Si alguna vez te has preguntado cómo hallar el área superficial o cuál es el área de la superficie lateral de un sólido, esta calculadora está aquí para ayudarte. El área superficial tiene una lista gigantesca de aplicaciones en todos los campos, como la aerodinámica.

En este artículo encontrarás las fórmulas del área superficial de una esfera, cubo, cilindro, cono, pirámide y prisma rectangular/triangular. También explicaremos cómo calcular el área superficial de una esfera a modo de ejemplo.

El área superficial es el área total que ocupa la superficie del objeto. En otras palabras, es el área total de la superficie de un objeto tridimensional.

A veces, el área superficial puede dividirse en una suma de áreas de la o las bases y área de la superficie lateral. La superficie lateral es el área de todos los lados del objeto, excluyendo su base y su parte superior. Esta división se utiliza para formas en las que hay una distinción obvia entre la base y la otra parte, por ejemplo, para un cilindro, un cono, una pirámide, o un prisma triangular. Rara vez se aplica a sólidos para los que no estamos seguros de qué caras deben tratarse como bases (como en un cubo o una caja), y no la utilizamos para superficies lisas como una esfera.

Nuestra calculadora de área superficial puede hallar el área superficial de siete sólidos diferentes. La fórmula depende del tipo de sólido.

• Área superficial de una esfera: A = 4πr², donde r es el radio de la esfera.

• Área superficial de un cubo: A = 6a², donde a es la longitud de alguna de sus aristas.

• Área superficial de un cilindro: A = 2πr² + 2πrh, donde r es el radio y h es la altura del cilindro.

• Área superficial de un cono: A = πr² + πr√(r² + h²), donde r es el radio y h es la altura del cono.

• Área superficial de un prisma rectangular (caja): A = 2(ab + bc + ac), donde a, b y c son las longitudes de tres lados del cuboide.

• Área superficial de un prisma triangular: A = 0.5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c), donde a, b y c son las longitudes de tres lados de la base del prisma triangular y h es una altura (longitud) del prisma.

• Área superficial de una pirámide: A = l × √(l² + 4 × h²) + l², donde l es la longitud de un lado de la base cuadrada y h es la altura de una pirámide.

Pero, ¿de dónde salen esas fórmulas? ¿Cómo hallar el área superficial de las formas tridimensionales básicas? ¡Sigue leyendo y lo descubrirás!

Para calcular el área superficial de una esfera, basta con conocer su radio o diámetro.

• A = 4 × π × r² donde r es el radio.

Como sabemos que el diámetro de una esfera es igual a dos radios (d = 2r), podemos transformar la ecuación en otra forma:

• A = 4 × π × (d/2)² = π × d², donde d es el diámetro de la esfera.

La derivación de esta fórmula del área superficial requiere integración. Si tienes curiosidad, consulta esta prueba.

Para averiguar el área superficial de un cilindro, debes tener dos valores: el radio (o diámetro) de una base y la altura del cilindro. La ecuación general es la habitual: área de las bases mas área de la superficie lateral. En nuestro caso, un círculo es una base.

• A = 2πr² + 2πrh

¿De dónde procede esta fórmula? Puedes escribir la ecuación del área superficial de un cilindro como:

• A = A(lateral) + 2 × A(base)

Es fácil hallar el área de la base: recordamos la conocida fórmula del área de un círculo: A(base) = π × r². Pero, ¿cuál es la forma del área de la superficie lateral? Intenta imaginar que la “desplegamos”. ¿Reconoces lo que resulta? ¡Es un rectángulo!, y la longitud de uno de sus lados es la altura del cilindro, y la del segundo es la longitud de la circunferencia del círculo desplegado (2 × π × r).

• A(base) = π × r²
• A(lateral) = h × (2 × π × r)

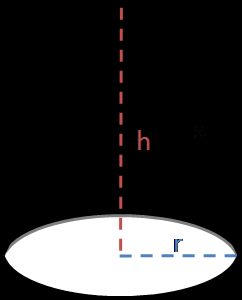
Podemos dividir el área superficial de un cono en dos partes:

• A = A(lateral) + A(base), ya que solo tenemos una base, a diferencia del cilindro.

La base es de nuevo el área de un círculo A(base) = π × r², pero la procedencia del área de la superficie lateral quizá no sea tan evidente:

• A(lateral) = π × r × √(r² + h²)

Veamos esta derivación paso a paso:

1. Despliega, en un plano, la superficie lateral. Esto resultará en un sector circular, es decir, la porción de un círculo de radio s (s es a su vez la altura de inclinación del cono).

2. Para el círculo de radio s, la circunferencia es igual a 2 × π × s. Por su parte, la longitud de arco del sector es igual a 2 × π × r.

3. El área de un sector —que es nuestra superficie lateral del cono— viene dada por la fórmula:

• A(lateral) = (s × longitud de arco)/2 = (s × 2 × π × r)/2 = π × r × s

  La fórmula puede obtenerse a partir de proporciones, ya que la razón entre las áreas de las formas es la misma que la razón entre la longitud de arco y la circunferencia:

  (área del sector)/(área del círculo grande) = (longitud de arco)/(circunferencia del círculo grande), por tanto:

  (área del sector)/(π × s²) = (2 × π × r) /(2 × π × s)

  (área del sector) = (π × s²) × (2 × π × r)/(2 × π × s)

• A(lateral) = π × r × s

  Para encontrar el término que falta en esta razón, ¡puedes intentar también con nuestra calculadora de razones!

4. Normalmente, no tenemos el valor s, sino h, que es la altura del cono. ¡Pero eso no es ningún problema! Podemos transformar fácilmente la fórmula utilizando teorema de Pitágoras:

• r² + h²= s² así que sacando la raíz cuadrada obtenemos s = √(r² + h²)

  Así, la fórmula del área de la superficie lateral es la siguiente:

• A(lateral) = π × r × √(r² + h²)

5. Por último, suma las áreas de la base y de la parte lateral para hallar la fórmula final del área superficial de un cono:

• A = A(lateral) + A(base) = π × r × s + π × r² (dados r y s)
  • o bien:
• A = π × r × √(r² + h²) + π × r² (dados r y h).

El área de un cubo 🇺🇸 es la cosa más fácil que podrías imaginar: ¡cada una de las caras es un cuadrado! Como cada cubo tiene seis caras cuadradas idénticas, el área superficial es igual a:

• A = 6 × (área lateral)

Como el área de un cuadrado es el producto de la longitud de sus lados (o el cuadrado de cualquiera de sus aristas), la fórmula final del área superficial de un cubo es:

• A = 6 × l², donde l es la longitud de un lado del cuadrado, también conocida como arista.

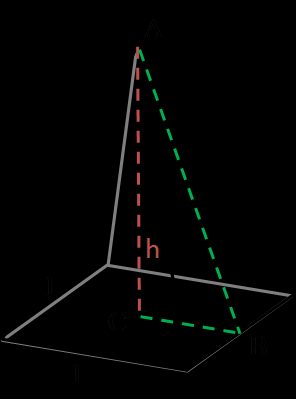
Una pirámide es un sólido tridimensional de base poligonal y caras laterales triangulares. Cuando oyes “una pirámide”, normalmente se supone que es una pirámide cuadrada regular. Pero dependiendo de la forma de la base, también podría ser una pirámide hexagonal o una pirámide rectangular. Regular significa que tiene una base de polígono regular y es una pirámide recta (vértice directamente sobre el centroide de su base), y cuadrada significa que tiene esta forma como base. Esa es la opción que utilizamos como pirámide en esta calculadora de área superficial.

La fórmula del área superficial de una pirámide es:

• A = l × √(l² + 4 × h²) + l² donde l es un lado de la base, y h es la altura de una pirámide

De nuevo, podemos dividir la ecuación en dos partes:

A = A(base) + A(lateral) = A(base) + 4 × A(cara lateral)

La base tiene forma de cuadrado, por lo que A(base) = l². Para calcular el área de la superficie lateral, partamos del área de una cara triangular:

1. Para hallar la altura del triángulo, necesitaremos de nuevo la fórmula de la hipotenusa:

   c = √(a² + b²)

2. Calcula la hipotenusa del triángulo ABC (que es al mismo tiempo la altura de la cara triangular):

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. El área de un triángulo (en nuestro caso, se trata de un triángulo isósceles) puede calcularse como:

   A = altura × base / 2, por lo que:

   A(cara lateral) = √(h² + l²/4) × l / 2

4. Por tanto, la fórmula final del área superficial de una pirámide es:

   A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)

   A = l² + l × √(4 × h² + l²)

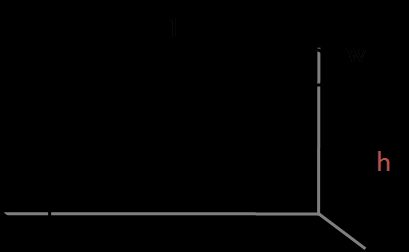
Para calcular el área superficial de un prisma rectangular, basta con calcular las áreas de los lados rectangulares:

• A = 2 × (A1 + A2 + A3)

donde:

• A1 = l × w
• A2 = w × h
• A3 = l × h

Por tanto, la fórmula final es:

• A = 2 × (l × w + w × h + l × h)

Para comprender de dónde procede la fórmula del área superficial de un prisma triangular, veamos esta derivación:

1. La parte del área de la superficie lateral es fácil de calcular en este caso. Como puedes ver en la imagen, está formado por tres rectángulos, con una longitud lateral en común:

   A(lateral) = a × h + b × h + c × h = h × (a + b + c)

   que también podemos escribir abreviadamente como

   A(lateral) = h × P, donde P es el perímetro de uno de los triángulos de la base.

2. A continuación, halla el área de una de las bases triangulares. Puedes hacerlo de muchas formas, dependiendo de lo que te den. En nuestra calculadora, hemos implementado el cálculo basándonos en la fórmula de Herón 🇺🇸, que se utiliza cuando tienes tres lados de triángulo dados (SSS).

   A(base) = 0.25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

3. Finalmente, la fórmula final del área superficial de un prisma triangular es:

   A = A(lateral) + 2 × A(base)

   A = h × (a + b + c) + 0.5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

Puedes calcular la superficie de cualquier sólido, por ejemplo, de tu cuerpo, ¡no hace falta que sea la forma simple de la geometría! Si tienes curiosidad por saber cuál es el área superficial externa de un cuerpo humano, consulta esta calculadora de superficie corporal.

Si quieres hallar el área superficial de una esfera, sigue estos pasos:

1. Determina el radio de la esfera. Podemos suponer un radio de 10 cm.

2. Introduce este valor en la fórmula:

   A = 4πr²

3. Calcula el resultado:

   A = 4π × (10 cm)² = 1256 cm²

4. También puedes utilizar nuestra calculadora de área superficial para hallar el radio de la esfera si conoces su área.

Las unidades de área superficial son siempre unidades cuadradas de longitud. Por ejemplo, puedes expresarla en cm², in², ft², m², pero también en acres y hectáreas.

Si quieres hallar el volumen de cualquiera de estos sólidos, utiliza nuestra calculadora de volumen para hacerlo.

Para convertir de área superficial a arista, sigue estos pasos:

1. Escribe el área de tu cubo.
2. Divídela por seis. El resultado es el área de una cara.
3. Saca la raíz cuadrada del número del paso 2.
4. Esta es la longitud de cada arista de tu cubo. ¡Bien hecho!

Para deducir el radio de una esfera a partir de su área superficial:

1. Escribe el área superficial de la esfera.
2. Divídela por 4π ≈ 12.5664.
3. Saca la raíz cuadrada: √(Área / 4π).
4. Ya está; ¡este es el radio! Puedes comprobar el resultado con una calculadora de área superficial.

La respuesta es 50.2655 centímetros cuadrados. Para obtener este resultado, recuerda que la fórmula del área superficial de un cilindro es:

Área = 2πr(r + h)

Introduciendo r = h = 2 cm, obtenemos Área = 16π cm² ≈ 50.2655 cm².

Como tanto r como h están en cm, el área está en cm².