Calculadora de la altura de un triángulo
Si buscas una herramienta sencilla para calcular la altura de cualquier triángulo, estás en el lugar correcto. Esta calculadora de la altura de un triángulo es la herramienta que necesitas. Ya sea que estés buscando las fórmulas de altura de triángulos especiales, como el triángulo rectángulo, equilátero o isósceles, o cualquier triángulo escaleno, esta calculadora te será de gran ayuda. Con ella puedes calcular la altura de un triángulo, así como los lados, ángulos, el perímetro y el área del triángulo.
Si aún te preguntas cuál es la fórmula de la altura de un triángulo equilátero o cómo hallar la altura sin el área, sigue leyendo y encontrarás la respuesta.
¿Cuál es la altura de un triángulo?
Cada lado de un triángulo puede considerarse como una base, y desde cada vértice puedes trazar una línea perpendicular a una recta que contenga la base. A esta línea perpendicular se la conoce como la altura del triángulo. Todos los triángulos tienen tres alturas en total. Dibujar la altura se conoce como "bajar la altura" en ese vértice.
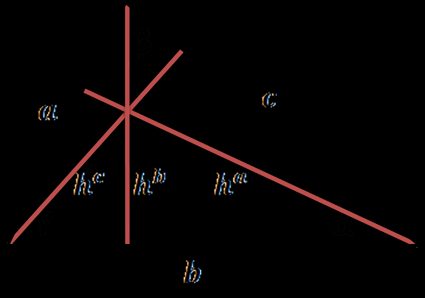
Cómo hallar la altura de un triángulo – fórmulas
Existen diversas maneras de encontrar la altura de un triángulo. La más común es utilizando el área del triángulo, pero también hay muchas otras fórmulas:
-
Dada el área del triángulo
La fórmula del área de un triángulo puede reordenarse para calcular la altura de un triángulo rectángulo:
-
, donde es la base, y la altura; y
-
Entonces .
-
-
Dados los lados del triángulo
Utilizando la fórmula de Herón, puedes calcular el área del triángulo cuando conoces los lados. Una vez que tienes el área, puedes utilizar la ecuación del área para encontrar la altura de un triángulo:
Fórmula de Herón:
Por tanto:
Puedes obtener más información sobre esta ecuación con nuestra calculadora de la fórmula de Herón 🇺🇸.
-
Dados dos lados y el ángulo entre ellos
Utiliza la trigonometría u otra fórmula para el área de un triángulo:
(o o si tienes diferentes caras dadas):
Si tu figura es un tipo de triángulo especial, desplázate hacia abajo para encontrar más fórmulas de la altura de un triángulo. Las versiones simplificadas de las ecuaciones generales son más fáciles de recordar y calcular.
Cómo hallar la altura de un triángulo equilátero
Un triángulo equilátero es un triángulo con los tres lados iguales y los tres ángulos iguales a . Las tres alturas tienen la misma longitud que puede calcularse a partir de:
- , donde es un lado del triángulo.
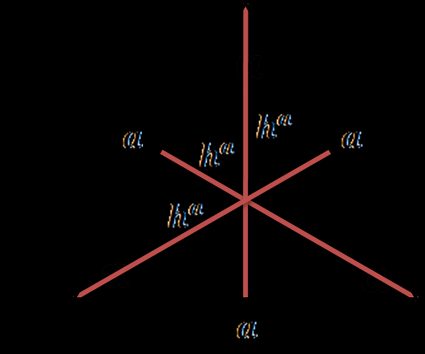
En un triángulo equilátero, las alturas, las bisectrices de los ángulos, las bisectrices perpendiculares, y las medianas, coinciden.
Si lo que buscas son las fórmulas del área y el perímetro, visita nuestra calculadora de triángulos equiláteros.
Cómo hallar la altura de un triángulo isósceles
Un triángulo isósceles es un triángulo con dos lados de igual longitud. Hay dos alturas diferentes de un triángulo isósceles; la fórmula para la del punto más alto es:
-
, donde es un cateto del triángulo, y es la base. La fórmula se deriva del teorema de Pitágoras.
-
Las alturas desde los vértices de la base se pueden calcular a partir de:
Fórmula del área:
Trigonometría:
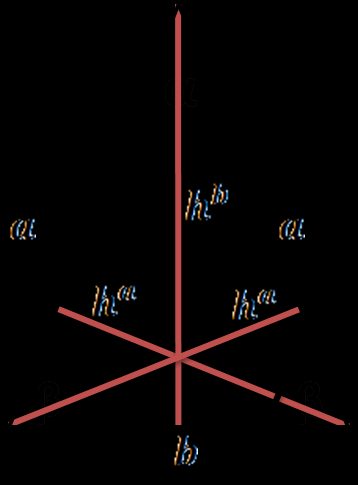
Para obtener las fórmulas del área y el perímetro de este tipo de triángulo, visita nuestra calculadora de triángulos isósceles.
Cómo hallar la altura de un triángulo rectángulo
Un triángulo rectángulo es un triángulo con un ángulo de . Es fácil encontrar dos de las alturas, ya que los catetos son perpendiculares: si consideramos el cateto más corto como una base, el cateto más largo se convierte en la altura, y viceversa. La tercera altura de un triángulo puede calcularse mediante la siguiente fórmula:

Si te interesan las ecuaciones del área y el perímetro de este triángulo, consulta nuestra calculadora de triángulos rectángulos.
¿Cómo hallar la altura de un triángulo con esta calculadora de la altura de un triángulo?
Después de leer nuestra explicación, estamos seguros de que ahora entiendes cómo calcular la altura de un triángulo sin conocer el área. Pero veamos un ejemplo sencillo para mostrarte la versatilidad de nuestra herramienta:
- Elige el tipo de triángulo. Supongamos que queremos calcular las alturas de un triángulo escaleno, así que no cambiamos la opción por defecto.
- Ingresa los valores conocidos. Pueden ser tres lados o dos lados y un ángulo. Quedémonos con la primera opción: , , .
- La calculadora de la altura de un triángulo mostrará las tres alturas: estas son , , y . Además, la calculadora proporcionará los ángulos del triángulo, el área y el perímetro.
Muy útil, ¿no?
Preguntas frecuentes
¿Cómo se halla la altura de un triángulo si todos sus lados son iguales?
Para determinar la altura de un triángulo equilátero:
- Escribe la longitud de los lados de tu triángulo.
- Multiplícala por
√3 ≈ 1.73. - Divide el resultado por
2. - Ya está, ¡el resultado es la altura de tu triángulo!
¿Son iguales todas las alturas de un triángulo?
Por lo general no; cada altura de un triángulo puede tener una longitud diferente. Sin embargo, si las tres alturas tienen longitudes iguales, entonces este triángulo es equilátero, es decir, todos sus lados son iguales entre sí (¡pero no iguales a las alturas!).
¿Cómo se halla la altura de un triángulo dados los ángulos?
No puedes determinar la altura de un triángulo solo conociendo sus ángulos. Esto se debe a que existen infinitos triángulos con los mismos ángulos, y las longitudes de las alturas en cada uno de esos triángulos varían.
¿Cómo se halla la altura de un triángulo rectángulo?
Cada uno de los lados perpendiculares (catetos) de un triángulo rectángulo es una de las alturas. Para calcular la tercera altura h3, utiliza la fórmula del área:
½ × cateto1 × cateto2 = área = ½ × hipotenusa × h3
En consecuencia:
h3 = cateto1 × cateto2 / hipotenusa
¿Cuál es la altura más corta del triángulo 3 4 5?
La respuesta es 2.4. Para llegar a este resultado, observa que el área es área = ½ × 3 × 4 = 6.
Por otra parte, área = ½ × hipotenusa × altura más corta.
Como hipotenusa = 5 y área = 6, obtenemos que la altura más corta = 2 × área / hipotenusa = 2 × 6 / 5 = 2.4.