Calculadora de triángulos rectángulos

La calculadora de triángulos rectángulos te ayudará a encontrar las longitudes de los lados de un triángulo rectángulo. Este solucionador de triángulos también te enseñará a hallar el área de un triángulo rectángulo, además de darte mucha información sobre las aplicaciones prácticas de un triángulo rectángulo.

Lo primero es lo primero, vamos a explicar qué es un triángulo rectángulo. La definición es muy sencilla e incluso puede parecer obvia para quienes ya la conocen: un triángulo rectángulo es un triángulo en el que uno y solo uno de los ángulos mide exactamente 90°. Los otros dos ángulos serán claramente menores que el ángulo recto, porque la suma de todos los ángulos de un triángulo es siempre 180°.

En un triángulo rectángulo, definimos los lados de un modo especial. El lado opuesto al ángulo recto es siempre el mayor del triángulo y recibe el nombre de “hipotenusa”. Los otros dos lados se llaman catetos. La relación entre la hipotenusa y cada cateto es sencilla, como veremos cuando hablemos del teorema de Pitágoras.

Si lo único que quieres calcular es la hipotenusa de un triángulo rectángulo, esta página y su calculadora de triángulos rectángulos funcionarán perfectamente. Sin embargo, también te recomendamos que utilices la herramienta específica que hemos desarrollado en Omni: la calculadora de hipotenusas. La hipotenusa está frente del ángulo recto y puede resolverse mediante el teorema de Pitágoras. En un triángulo rectángulo con catetos a y b y con hipotenusa c, el teorema de Pitágoras establece que: a² + b² = c².

Para resolver c, toma la raíz cuadrada de ambos lados para obtener c = √(b²+a²). Podemos considerar esta ampliación del teorema de Pitágoras como una “fórmula de la hipotenusa”. Una calculadora del teorema de Pitágoras también resulta excelente para calcular la hipotenusa.

Resolvamos ahora un ejemplo práctico de lo que supondría calcular la hipotenusa de un triángulo rectángulo sin utilizar ninguna calculadora disponible en Omni:

1. Obtén los valores de a y b.
2. Eleva al cuadrado a y b.
3. Suma ambos valores: a² + b².
4. Saca la raíz cuadrada del resultado.
5. La raíz cuadrada dará resultados positivos y negativos. Como se trata de longitudes, ignora el negativo.
6. El valor resultante es el valor de la hipotenusa c.

Veamos ahora cómo sería el proceso utilizando una de las calculadoras de Omni, como la calculadora de triángulos rectángulos de esta página web:

1. Introduce el valor de a y b en la calculadora.
2. Obtén inmediatamente el valor de c.
3. Como extra, obtendrás el valor del área de dicho triángulo.

Ya hemos visto que calcular el área de un triángulo rectángulo es muy fácil con la calculadora de triángulos rectángulos. En Omni, también tenemos una calculadora diseñada específicamente para ese fin: calculadora del área de un triángulo rectángulo. Veamos ahora un poco más en profundidad cómo calcular áreas de triángulos rectángulos.

El método para hallar el área de un triángulo rectángulo es bastante sencillo. Todo lo que necesitas son las longitudes de la base y la altura. En un triángulo rectángulo, la base y la altura son los dos lados que forman el ángulo recto. Como multiplicando estos dos valores se obtendría el área del rectángulo correspondiente, y el triángulo es la mitad de este, la fórmula es:

área = ½ × base × altura.

Si no conoces la base ni la altura, puedes hallarla mediante el teorema de Pitágoras. Prueba la calculadora de triángulos rectángulos para comprobar tus cálculos o calcula el área de triángulos cuyos lados tengan longitudes mayores o con valores decimales.

Ahora vamos a ver otras cosas que se pueden calcular a partir de un triángulo rectángulo utilizando algunas de las herramientas disponibles en Omni. Los lados de un triángulo tienen un determinado gradiente o pendiente. La fórmula de la pendiente es:

Pendiente = (y₂ - y₁)/(x₂ - x₁).

Por tanto, si las coordenadas son (1,-6) y (4,8), la pendiente del segmento es (8 + 6)/(4 - 1) = 14/3. Una forma fácil de determinar si el triángulo es rectángulo, y solo conoces las coordenadas, es ver si las pendientes de dos rectas cualesquiera se multiplican para ser iguales a -1.

Hay una forma fácil de convertir ángulos de radianes a grados y de grados a radianes con el uso de la conversión de ángulos:

• Si un ángulo está en radianes, multiplícalo por 180/π; y
• Si un ángulo está en grados, multiplícalo por π/180.

A veces puedes encontrarte con un problema en el que falten las longitudes de dos o incluso tres lados. En tales casos, la calculadora de triángulos rectángulos, la calculadora de hipotenusas y el método sobre cómo hallar el área de un triángulo rectángulo no te serán de ayuda. Tienes que utilizar funciones trigonométricas para resolver estas piezas faltantes.

El triángulo rectángulo es solo uno de los muchos triángulos especiales que existen. Estos triángulos tienen una o varias características especiales que los hacen únicos. Por ejemplo, como hemos visto, el triángulo rectángulo tiene un ángulo recto y, por tanto, una hipotenusa, lo que lo convierte en un tipo único de triángulo. Aparte del triángulo rectángulo, hay otros triángulos especiales con propiedades interesantes.

Uno de los triángulos especiales más conocidos es el triángulo equilátero, que tiene tres lados iguales y todos sus ángulos son de 60°. Esto hace que sea mucho más sencillo que una calculadora de triángulos evalúe distintos parámetros de un triángulo de este tipo.

Otro de los triángulos especiales es el triángulo isósceles, que tiene 2 lados de igual longitud, y, por tanto, dos ángulos del mismo tamaño. A diferencia del triángulo equilátero, los triángulos isósceles tienen muchas formas diferentes.

Hay muchos otros triángulos especiales. Sin embargo, a continuación veremos algunos triángulos rectángulos muy especiales que, además de ser triángulos rectángulos, tienen otras propiedades únicas que los hacen interesantes.

El llamado triángulo “45-45-90” es probablemente el más especial entre todos los triángulos rectángulos especiales. Se trata de un triángulo rectángulo que también es un triángulo isósceles. Sus dos catetos tienen la misma longitud (isósceles), y además tiene la peculiaridad de que los ángulos no rectos miden exactamente la mitad que el ángulo recto que da nombre al triángulo rectángulo.

Este triángulo rectángulo es el tipo de triángulo que puedes obtener cuando divides un cuadrado por su diagonal. Por eso ambos catetos (lados del cuadrado) tienen la misma longitud. A los interesados en saber más sobre el más especial de los triángulos rectángulos especiales, les recomendamos que consulten la calculadora de triángulos 45-45-90, hecha con este fin.

Otro triángulo fascinante del grupo de los triángulos rectángulos especiales es el llamado triángulo “30-60-90”. El nombre se debe a que tiene un ángulo recto (90°), luego un ángulo de 30° y otro de 60°. Estos ángulos son especiales por los valores de sus funciones trigonométricas (coseno, seno, tangente, etc.). Las consecuencias de esto se pueden ver y comprender con la calculadora de triángulos 30-60-90, pero para los que les dé un poco de pereza hacer clic en el enlace, resumiremos aquí algunas de ellas. Suponiendo que el lado más corto es de longitud a, el triángulo sigue:

1. La segunda longitud es igual a a√3.
2. La hipotenusa es 2a.
3. El área es igual a (a²√3)/2.
4. El perímetro es igual a a(3 + √3).

A primera vista puede parecer que un triángulo rectángulo y un paralelogramo no tienen nada en común. ¿Cómo puede ayudarte un solucionador de triángulos a entender un paralelogramo? La realidad es que cualquier paralelogramo puede descomponerse en 2 o más triángulos rectángulos. Tomemos como ejemplo el rectángulo, que es el más fácil de ver.

Imagina un rectángulo cualquiera. Dibuja ahora un trazo sobre una de las diagonales de este rectángulo. Si separamos el rectángulo por la diagonal, obtendremos dos triángulos rectángulos. Observando los triángulos, no hace falta utilizar la calculadora de triángulos rectángulos para ver que ambos son iguales, por lo que sus áreas serán iguales. Esto significa que el área del rectángulo es el doble que la de cada triángulo.

Si pensamos en las ecuaciones, tiene sentido, ya que el área de un rectángulo de lados a y b es exactamente área = a × b, mientras que para el triángulo rectángulo es área = base × altura / 2 que, en este caso, significaría área = a × b /2. Esto es precisamente lo que ya vimos cortando el rectángulo por la diagonal.

Era un ejemplo sencillo de rectángulo, pero lo mismo se aplica al área de un cuadrado. Para otros paralelogramos, el proceso se complica un poco más (puede implicar hasta 4 triángulos rectángulos de distintos tamaños). Aun así, con un poco de habilidad, puedes utilizar la misma idea y calcular el área de un paralelogramo utilizando triángulos rectángulos. Por supuesto, puedes ser aún más eficiente y usar simplemente nuestra calculadora.

La geometría y los polígonos, especialmente los triángulos, siempre van de la mano. Las propiedades de algunos triángulos, como los rectángulos, suelen ser interesantes e impactantes, incluso para los no matemáticos. A continuación veremos un interesante conjunto de números, muy relacionados con los triángulos rectángulos, y que los matemáticos (y quizá a tú también) aman.

Estos conjuntos de números se llaman ternas pitagóricas y son conjuntos de 3 números enteros (llamémoslos a, b y c) y satisfacen el teorema de Pitágoras: a² + b² = c². Es decir, pueden formar un triángulo rectángulo con lados de longitud a, b y c. La cantidad de números que satisfacen esta relación es limitada, pero a los matemáticos les divierte buscar nuevos de estos.

Aparte del factor curiosidad de esta relación, tiene algunas propiedades interesantes que se explotan en criptografía. Dadas las aplicaciones que se podrían encontrar para tales conjuntos de números, los matemáticos han explorado incluso más allá, utilizando 4, 5… y más conjuntos de números que satisfacen una relación similar en la que la suma de los cuadrados de todos los números, excepto uno, da el cuadrado del número que queda.

También está muy relacionado con estas ternas pitagóricas el infame último teorema de Fermat, en el que el casi legendario matemático críptico Pierre Fermat afirmó que no podía haber un conjunto de tres números enteros que satisficiera la relación aⁿ + bⁿ = cⁿ para n mayor que 2. Esta conjetura no se demostró hasta 1995, más de 300 años después de su formulación, y se considera uno de los problemas matemáticos más importantes del siglo.

Hemos hablado mucho de triángulos, sobre todo de triángulos rectángulos, y de sus aplicaciones en matemáticas y geometría. De lo que aún no hemos hablado es de la utilidad de los triángulos rectángulos para calcular cosas en la vida real. Puede parecer que las aplicaciones fuera de la geometría son limitadas, pero echemos un vistazo a las sombras.

Sí, las sombras. La sombra oscura que proyecta un objeto cuando está iluminado. Si observaras la forma que forman la sombra, el objeto y el suelo, te darías cuenta de que, de hecho, ¡es un triángulo rectángulo! Al menos, lo es cuando el objeto está perfectamente vertical y el suelo horizontal. La mayoría de las veces es así, o al menos se aproxima bastante. Esto significa que podemos utilizar la calculadora de triángulos rectángulos para encontrar distintos datos sobre los objetos bajo el sol. Veamos cómo.

Imagina que tienes un edificio del que queremos saber la altura, pero no puedes medirlo directamente porque es demasiado alto para dejar caer una cinta métrica desde lo alto. Lo que puedes hacer es medir la longitud de la sombra en la calle. Luego, con la ayuda de cualquier herramienta de medición de ángulos y un trozo de papel, puedes averiguar el ángulo entre la sombra y el suelo. Sabiendo que el ángulo entre el edificio y el suelo es de 90°, puedes obtener el valor de la altura del edificio.

Usando esta técnica, puedes medir la altura de muchos objetos siempre que tengas un día soleado u otras fuentes de luz para iluminar el objeto. De hecho, esta solía ser una técnica de medición muy común antiguamente. Probablemente, el uso más interesante y alucinante de los triángulos rectángulos sea el de Eratóstenes, que consiguió utilizar triángulos rectángulos y sombras para medir el radio de la Tierra, y ahora vamos a explicar cómo lo hizo.

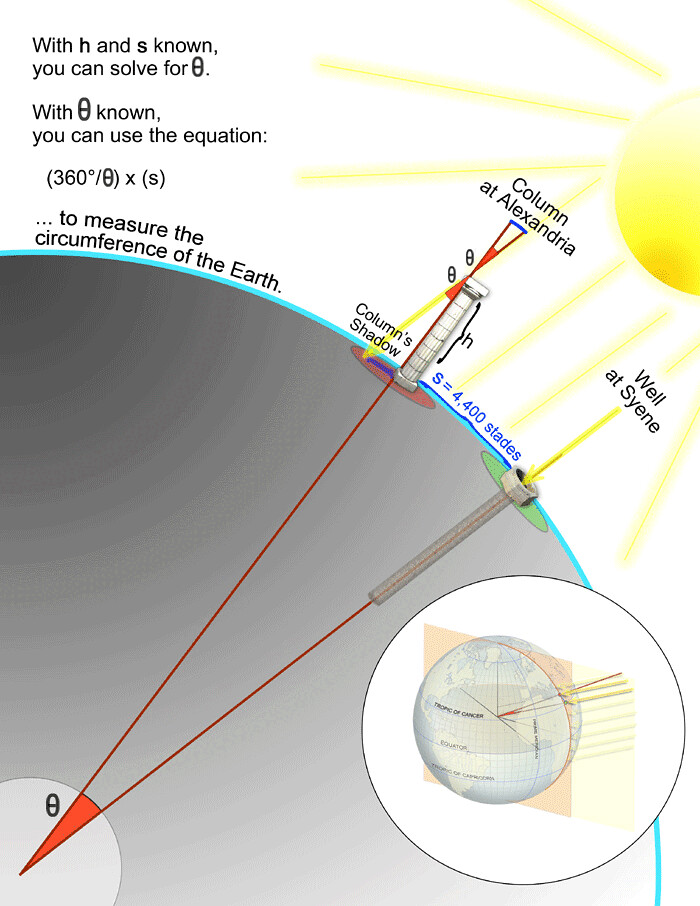
Eratóstenes observó que en el solsticio de verano había un lugar en la Tierra donde los pozos no tenían sombra al mediodía, es decir, el sol brillaba directamente sobre ellos. Observando esto, colocó una columna de una altura conocida a una distancia conocida de ese pozo y midió el tamaño de la sombra creada por el poste al mediodía del día del solsticio. Luego, utilizando triángulos rectángulos y trigonometría, pudo determinar el ángulo que va desde el centro de la Tierra entre el pozo y el poste, así como el radio de la Tierra, basándose en la distancia conocida entre estos dos puntos.

Fue una hazaña asombrosa que ahora puedes lograr mucho más fácilmente, con solo usar las calculadoras Omni que hemos hecho para ti.