Última actualización: 27 de Jul. de 2024

Calculadora del área de un triángulo rectángulo

Q: ¿Cuál es el área de un triángulo rectángulo con hipotenusa de 5 cm y ángulo de 45°?

El área es 6.25 . Obtenemos esta respuesta aplicando la fórmula área = c² × sen(α) × cos(α) / 2 con c = 5 y α = 45° . El teorema matemático utilizado para obtener esta fórmula se llama ley de los senos .

Q: ¿Cómo llamamos a los lados de un triángulo rectángulo?

Los dos lados perpendiculares entre sí se llaman catetos . El lado opuesto al ángulo recto (es decir, el lado más largo) es la hipotenusa .

Índice general

Fórmulas del área de un triángulo rectángulo Área de un triángulo rectángulo isósceles Cómo usar la calculadora del área de un triángulo rectángulo Preguntas frecuentes

Si te preguntas cómo calcular el área de un triángulo rectángulo, estás en el lugar adecuado: esta calculadora del área de un triángulo rectángulo es la herramienta para ti.

Tanto si buscas la ecuación dados los catetos del triángulo, el cateto y la hipotenusa, o el lado y el ángulo, no te decepcionará: esta calculadora las tiene todas implementadas.

Desplázate hacia abajo para saber más sobre las fórmulas del área de un triángulo rectángulo, ¡o simplemente para probar nuestra calculadora!

Fórmulas del área de un triángulo rectángulo

🙋 Si acabas de darte cuenta de que tu triángulo no es un triángulo rectángulo, consulta esta calculadora del área de triángulos.

La ecuación básica es una versión transformada de la fórmula de la altura de un triángulo ( $a \cdot h / 2$ ). Como los catetos del triángulo rectángulo son perpendiculares entre sí, uno de los catetos se toma como base y el otro como altura del triángulo rectángulo:

\text{área}=\frac{a\cdot b}{2}

A veces no es tan fácil: tienes otros valores dados, no dos catetos. ¿Entonces qué?

Si tienes un cateto y una hipotenusa dados, utiliza el teorema de Pitágoras para encontrar el cateto que falta:

\qquad a^2+b^2=c^2

A continuación, calcula la raíz cuadrada de la ecuación transformada:

Dados $a$ y $c$ encontramos que $b = \sqrt{c^2 - a^2}$ :

\qquad\text{area}=a\cdot\frac{\sqrt{c^2-a^2}}{2}

Dados $b$ y $c$ calculamos que $a = \sqrt{c^2 - b^2}$ :

\qquad \text{area} = b\cdot\frac{\sqrt{c^2-b^2}}{2}

Si conoces un ángulo y la hipotenusa, puedes aplicar la ley de los senos sobre este triángulo:

\qquad a=c\cdot\text{sen}(\alpha)

Por tanto:

\qquad \begin{split} b&=c\cdot\text{sen}(\beta)\\&=c\cdot\text{sen}(90\degree-\alpha)\\ &=c\cdot\cos(\alpha) \end{split}

Así:

\qquad \text{area}=c^2\cdot\text{sen}(\alpha)\cdot\frac{\cos(\alpha)}{2}

Dados un ángulo y un cateto, puedes calcular el área utilizando, por ejemplo, funciones trigonométricas:

\qquad\frac{a}{b}=\tan(\alpha)

\qquad\frac{b}{a}=\tan(\beta)

Encontramos:

\qquad \begin{split} \text{area}&=b\cdot\tan(\alpha)\cdot\frac{b}{2}\\ \\[1.5em] &=b^2\cdot\frac{\tan(\alpha)}{2} \end{split}

\qquad \begin{split} \text{area}&=a\cdot a\cdot \frac{\tan(\beta)}{2}\\[1em] &=a^2\cdot\frac{\tan(\beta)}{2} \end{split}

🙋 ¿Quieres saber más sobre triángulos rectángulos? ¡Visita nuestra calculadora de triángulos rectángulos!

Área de un triángulo rectángulo isósceles

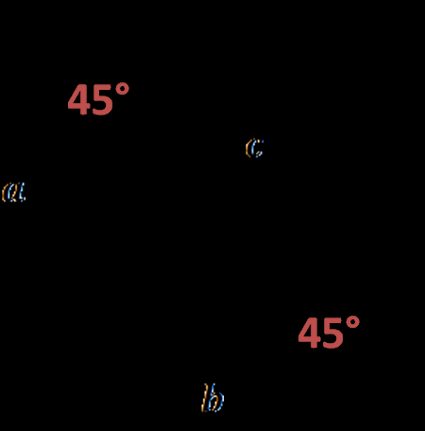
Un triángulo rectángulo isósceles es un triángulo rectángulo especial, a veces llamado triángulo 45-45-90 (es tan especial que hemos creado una herramienta sólo para él, la calculadora de triángulos 45-45-90). En un triángulo de este tipo, los catetos tienen la misma longitud (ya que la hipotenusa siempre debe ser el más largo de los lados del triángulo rectángulo):

a=b

Un cateto es la base y el otro es la altura: entre ellos hay un ángulo recto. Por tanto, el área de un triángulo rectángulo isósceles es:

\text{area}=\frac{a^2}{2}

Cómo usar la calculadora del área de un triángulo rectángulo

Vamos a mostrar el cálculo paso a paso:

Elige una opción, según los datos que tengas. Supongamos que conocemos un cateto y un ángulo, así que cambiamos la selección a ángulo dado y un lado.
Introduce los valores. Por ejemplo, sabemos que $\alpha = 40\degree$ y $b$ es $17\ \text{cm}$ .
¡Observa cómo nuestra calculadora del área de un triángulo rectángulo realiza todos los cálculos por ti! El área del triángulo elegido es $121.25\ \text{cm}^2$ .

Preguntas frecuentes

¿Cómo hallo el área de un triángulo rectángulo dados sus lados?

El método depende de los lados que te den:

Si conoces los dos catetos, utiliza la fórmula área = a × b / 2, donde a y b son los catetos.
Si conoces un cateto a y la hipotenusa c, utiliza la fórmula área = a × √(c² - a²) / 2.

¿Cuál es el área de un triángulo rectángulo con hipotenusa de 5 cm y ángulo de 45°?

El área es 6.25. Obtenemos esta respuesta aplicando la fórmula área = c² × sen(α) × cos(α) / 2 con c = 5 y α = 45°. El teorema matemático utilizado para obtener esta fórmula se llama ley de los senos.

¿Cómo sé si es un triángulo rectángulo?

Si te dan tres lados de un triángulo y quieres saber si este triángulo es rectángulo, comprueba si se cumple la fórmula pitagórica: a² + b² = c², donde c es el lado más largo y a y b son otros dos lados.

¿Cómo llamamos a los lados de un triángulo rectángulo?

Los dos lados perpendiculares entre sí se llaman catetos. El lado opuesto al ángulo recto (es decir, el lado más largo) es la hipotenusa.