Calculadora de raíz cuadrada

Con la calculadora de raíces cuadradas te ayuda a saber cuál es la raíz cuadrada de cualquier número y te permite sacar fácilmente la raíz cuadrada de cualquier número positivo que desees. Sólo tienes que introducir el número elegido y leer los resultados. ¡Todo se calcula rápida y automáticamente! Con esta herramienta, también puedes calcular el cuadrado del número deseado (sólo tienes que introducir el valor en el segundo campo), lo que puede ser de gran ayuda para encontrar cuadrados perfectos a partir de la fórmula de la raíz cuadrada.

¿Tienes problemas con las operaciones aritméticas básicas: sumar raíces cuadradas, restar raíces cuadradas, multiplicar raíces cuadradas o dividir raíces cuadradas? ¡Pues ya no! En el siguiente texto encontrarás una explicación detallada sobre distintas propiedades de la raíz cuadrada, por ejemplo, cómo simplificar raíces cuadradas, con varios ejemplos. Además, con esta calculadora de raíces cuadradas podrás sacar raíces cuadradas fácilmente sin hacer cálculos a mano.

Te contaremos también qué es y cómo calcular la raiz de un número negativo, te mostraremos ejemplos de raíces cuadradas exactas y no decimales y aprenderás a calcular la raíz cuadrada de cualquier número. Ademásss, si buscas la gráfica de la raíz cuadrada o las propiedades de la función raíz cuadrada, tenemos una sección entera para ti (como puedes ver en la tabla de contido arriba).

Por último, si no necesitas aprender cómo sacar la raíz de un número y sólo quieres tener las raíces ya calculadas, tenemos una gran lista de resultados para que puedas buscar la respuesta a tus preguntas sin tener que calcular la raíz cuadrada exacta de un número.

Si lo único que necesitas es saber cuál es la raíz cuadrada de un número y no quieres liarte aprendiendo cómo sacar la raíz cuadrada de un número, no te preocupes. Nuestra calculadora de raíces cuadradas puede calcular raices cuadradas por tí rápida y fácilmente. Veamos cómo:

1. Abre la página de Omnicalculator de la calculadora de raíces cuadradas. (Si estás leyendo esto, probablemente ya has completado el primero paso)
2. Haz click con el ratón en la primera casilla de entrada de datos; la que dice "Número".
3. Teclea el número del cuál quieres calcular la raíz cuadrada
4. ¡Ya está! La calculadora de raíz cuadrada te mostrará el resultado al momento en la casilla de debajo; llamada "Raíz cuadrada"

Parece mágia, ¿verdad? Nunca ha sido tan fácil saber cuál es la raíz cuadrada de cualquier número.

Si has introducido un número que no es un cuadrado perfecto, habrás visto que el resultado tiene muchos decimales y aparece un texto extra debajo. Este texto muestra el resultado exacto de la raíz cuadrada del número que has puesto, pero quizás no tiene la forma que esperabas.

No todos los números tienen una raíz cuadrada exacta. Esto nos deja dos opciones: aproximar el resultado con decimales, o indicar la raíz del número en cuestión como un factor de otra raíz cuadrada más pequeña. La calculadora de raíces cuadradas te ofrecen ambas opciones a la vez para que escojar cuál se adapta mejor a tus necesidades.

Explicaremos en detalle más adelante por qué existen raíces cuadradas no exactas y cómo resolverlas a mano, sin usar la calculadora de raíces cuadradas de Omni Calculator. Pero antes de nada, veamos qué es la raíz cuadrada.

La raíz cuadrada o raíz matemática es una operación que se realiza sobre un número para hallar el número que multiplicado por si mismo nos da el número inicial. Sacar la raíz cuadrada o calcular la raíz cuadrada de un número es la operación inversa a elevar un número al cuadrado. Esta es la definición más coloquial, pero veamos ahora qué es la raíz cuadrada de una forma más técnica.

La raíz cuadrada de un número dado x es todo número y cuyo cuadrado y² = y × y da como resultado el número original x. Por tanto, la fórmula de la raíz cuadrada puede expresarse como

√x = y ⟺ x = y²,

donde ⟺ es un símbolo matemático que significa si y sólo si. Cada número real positivo tiene siempre dos raíces cuadradas: la primera es positiva y la segunda negativa. Sin embargo, para muchos fines prácticos, solemos utilizar la positiva. El único número que tiene una raíz cuadrada es el cero. Esto se debe a que √0 = 0, y el cero no es ni positivo ni negativo.

También existe otra notación común de las raíces cuadradas que podría ser más conveniente en muchos cálculos complejos. Esta fórmula alternativa de la raíz cuadrada dice que la raíz cuadrada de un número es un número elevado al exponente de la fracción un medio:

√x = x^(1/2) = x^0.5

En interpretación geométrica, la raíz cuadrada del área de un cuadrado da la longitud de su lado. Por eso √ lleva la palabra cuadrado en su nombre. Algo parecido ocurre con la raíz cúbica, ∛. Si tomas la raíz cúbica del volumen de un cubo, obtienes la longitud de sus aristas. Mientras que las raíces cuadradas se utilizan cuando se consideran áreas superficiales, las raíces cúbicas son útiles para determinar cantidades relacionadas con el volumen, por ejemplo, la densidad.

La mejor forma de sacar la raíz cuadrada es usando nuestra calculadora de raices cuadradas. Puedes utilizarla tanto en tu computadora como en tu smartphone para calcular rápidamente la raíz cuadrada de un número dado. Por desgracia, a veces hay situaciones en las que sólo puedes confiar en ti mismo. ¿Y entonces qué? Para prepararte para ello, debes recordar varias raíces cuadradas perfectas básicas:

• Raíz cuadrada de 1: √1 = 1, ya que 1 × 1 = 1.

• Raíz cuadrada de 4: √4 = 2, ya que 2 × 2 = 4.

• Raíz cuadrada de 9: √9 = 3, ya que 3 × 3 = 9.

• Raíz cuadrada de 16: √16 = 4, ya que 4 × 4 = 16.

• Raíz cuadrada de 25: √25 = 5, ya que 5 × 5 = 25.

• Raíz cuadrada de 36: √36 = 6, ya que 6 × 6 = 36.

• Raíz cuadrada de 49: √49 = 7, ya que 7 × 7 = 49.

• Raíz cuadrada de 64: √64 = 8, ya que 8 × 8 = 64.

• Raíz cuadrada de 81: √81 = 9, ya que 9 × 9 = 81.

• Raíz cuadrada de 100: √100 = 10, ya que 10 × 10 = 100.

• Raíz cuadrada de 121: √121 = 11, ya que 11 × 11 = 121.

• Raíz cuadrada de 144: √144 = 12, ya que 12 × 12 = 144.

Los números anteriores son las raíces cuadradas exactas y son más sencillas, porque cada vez obtienes un número entero. ¡Intenta recordarlas! Pero, ¿qué puedes hacer cuando hay un número que no tiene una raíz cuadrada exacta? Lo más fácil es usar la calculadora de raíces cuadradas, pero si no tienes acceso a ella, hay múltiples soluciones. En primer lugar, puedes intentar predecir el resultado por ensayo y error. Digamos que quieres calcular la raíz cuadrada de 52:

1. Sabes que √49 = 7 y √64 = 8, así que √52 debería estar entre 7 y 8.

2. El número 52 está más cerca del 49 (su raíz, más cerca del 7), así que puedes intentar adivinar que √52 es 7.3.

3. Entonces, elevas al cuadrado 7.3, obteniendo 7.3² = 53.29 (como dice la fórmula de la raíz cuadrada), que es mayor que 52. Tienes que intentarlo con un número más pequeño, digamos 7.2.

4. El cuadrado de 7.2 es 51.84. Ahora tienes un número más pequeño, pero mucho más cercano al 52. Si esa precisión te satisface, puedes terminar aquí la estimación. Si no, puedes repetir el procedimiento con un número entre 7.2 y 7.3; por ejemplo, 7.22, y así sucesivamente.

Otro método consiste en simplificar primero la raíz cuadrada y luego utilizar las aproximaciones de las raíces cuadradas de los números primos (normalmente redondeadas a dos decimales). Aquí tienes ejemplos de la raíz cuadrada de algunos números primos:

• Raíz cuadrada de 2: √2 ≈ 1.41,
• Raíz cuadrada de 3: √3 ≈ 1.73,
• Raíz cuadrada de 5: √5 ≈ 2.24,
• Raíz cuadrada de 7: √7 ≈ 2.65,
• Raíz cuadrada de 11: √11 ≈ 3.32,
• Raíz cuadrada de 13: √13 ≈ 3.61,
• Raíz cuadrada de 17: √17 ≈ 4.12,
• Raíz cuadrada de 19: √19 ≈ 4.34, etc.

Volvamos a intentar hallar la raíz cuadrada de 52. Puedes simplificarla a √52 = 2√13 (aprenderás a simplificar la raíz cuadrada en el siguiente apartado) y luego sustituirla por √13 ≈ 3.61. Por último, haz una multiplicación √52 ≈ 2 × 3.61 = 7.22. ¡El resultado es el mismo que antes!

Ahora que ya hemos aprendido qué es la raíz cuadrada y cómo sacar la raíz cuadrada de un número a mano, volvamos a la calculadora que nos ocupa para entender bien sus ventajas.

Antes mencionamos que la calculadora de raíces cuadradas da tanto un resultado decimal (aproximado) como el resultado exacto como producto de raíces de números más pequeños. Como ya sabes cómo convertir una forma en otra, y entiendes perfectamente que son equivalentes, es momento de ver cuándo es una más útil que la otra.

Por ejemplo, si queremos calcular la raíz cuadrada de un número para luego seguir operando con él, nos puede interesar más el valor exacto ya que nos evita acarrear errores en los cómputos futuros, por eso la calculadora de raíces cuadradas te proporciona este valor adicional. Sin embargo, si queremos saber cuál es la raíz de nuestro número como resultado final (por ejemplo, calcular el lado de un cuadrado a partir de su área) entonces preferiremos la raíz aproximada en forma decimal.

Es por eso que nuestra calculadora de raíces cuadradas te calcula la raíz de cualquier número de ambas formas, tú escoges cuál es más útil. Recuerda, también, que nuestra calculadora recalcula automáticamente los números introducidos en cualquiera de los campos. Puedes sacar la raíz cuadrada de un número concreto rellenando el primer cuadro de entrada u obtener el cuadrado de un número que hayas introducido en el segundo. Por ejemplo, si introduces 17 en el segundo campo, descubrirás que 17² = 289, es decir, 289 es un cuadrado perfecto.

En primer lugar, vamos a preguntarnos qué raíces cuadradas pueden simplificarse. Para saberlo, debes tomar el número que está después del símbolo de la raíz cuadrada y encontrar sus factores. Si alguno de sus factores son cuadrados perfectos (4, 9, 16, 25, 36, 49, 64, etc.), entonces puedes simplificar la raíz cuadrada. ¿Por qué estos números son cuadrados perfectoss? Se pueden expresar respectivamente como 2², 3², 4², 5², 6², 7², etc. Veamos algunos ejemplos:

• ¿Puedes simplificar √27? Los factores de 27 son: 1, 3, 9, 27. ¡Aquí está el 9! Esto significa que puedes simplificar √27.

• ¿Puedes simplificar √15? Los factores de 15 son 1, 3, 5 y 15. No hay cuadrados perfectos en esos números, así que esta raíz cuadrada no se puede simplificar.

Entonces, ¿cómo simplificar raíces cuadradas? Para explicarlo, utilizaremos una práctica propiedad de la raíz cuadrada de la que hemos hablado antes; la fórmula alternativa de la raíz cuadrada:

√x = x^(1/2)

Podemos utilizar esas dos formas de expresar una raíz cuadrada y alternar entre ellas siempre que queramos. En particular, recordamos que la multiplicación de dos números elevados a la misma potencia, es equivalente a multiplicar ambos números y luego elevar el resultado a la potencia dada. Por tanto, podemos escribir:

(x × y)^(1/2) = x^(1/2) × y^(1/2) ⟺ √(x × y) = √x × √y,

¿Cómo utilizo esto para calcular la raíz cuadrada? El argumento de una raíz cuadrada no suele ser un cuadrado perfecto que puedas calcular fácilmente, pero puede contener un cuadrado perfecto entre sus factores. En otras palabras, puedes escribirlo como una multiplicación de varios números, donde uno (o más) de esos números es un cuadrado perfecto, por ejemplo, 45 = 9 × 5 (9 es un cuadrado perfecto). El requisito de tener al menos un factor que sea un cuadrado perfecto es necesario para poder simplificar la raíz cuadrada. Llegados a este punto, tienes que poner esta multiplicación bajo la raíz cuadrada. En nuestro ejemplo

√45 = 45^(1/2) = (9 × 5)^(1/2) = 9^(1/2) × 5^(1/2) = √9 × √5 = 3√5.

¡Has simplificado con éxito la primera raíz cuadrada! Por supuesto, no hace falta que escribas todos estos cálculos. Mientras recuerdes que la raíz cuadrada equivale a elevar un número a 1/2, puedes acortarlos. Practiquemos la simplificación de raíces cuadradas con otros ejemplos. ¿Sabrías cómo sacar la raíz cuadrada de estos números, en la forma simplificada?:

• ¿Cómo simplificar la raíz cuadrada de 27?

  √27 = √(9 × 3) = √9 × √3 = 3√3

• ¿Cómo sacar la raíz cuadrada de 8 simplificada?

  √8 = √(4 × 2) = √4 × √2 = 2√2

• ¿Cómo se saca la raíz cuadrada simplificada de 144?

  √144 = √(4 × 36) = √4 × √36 = 2 × 6 = 12

En el último ejemplo, no has tenido que simplificar la raíz cuadrada en absoluto porque 144 es un cuadrado perfecto. Te bastaba con recordar que 12 × 12 = 144. Sin embargo, queríamos mostrarte que, con el proceso de simplificación, también puedes sacar fácilmente las raíces cuadradas de cuadrados perfectos. Es útil cuando tratas con números grandes.

Por último, puedes preguntar cómo simplificar raíces de órdenes superiores, por ejemplo, raíces cúbicas 🇺🇸. De hecho, el proceso es muy análogo al de las raíces cuadradas, pero en el caso de las raíces cúbicas, tienes que encontrar al menos un factor que sea un cubo perfecto, no un cuadrado perfecto, es decir, 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ y así sucesivamente. Entonces divides tu número en dos partes y las colocas bajo la raíz cúbica. Tomemos el siguiente ejemplo de simplificación ³√192:

∛192 = ∛(64 × 3) = ∛64 × ∛3 = 4∛3

Puede parecer un poco complicado a primera vista, pero después de un poco de práctica, serás capaz de simplificar las raíces en tu cabeza. ¡Confía en nosotros!

Sumar raíces cuadradas y restar raíces cuadradas

Por desgracia, sumar o restar raíces cuadradas no es tan fácil como sumar/restar números normales. Por ejemplo, si 2 + 3 = 5, no significa que √2 + √3 sea igual a √5. **Para entenderlo, imagina que tienes dos tipos de figuras diferentes: triángulos 🔺 y círculos 🔵. ¿Qué ocurre cuando añades un triángulo a un círculo 🔺 + 🔵? ¡Nada! Sigues teniendo un triángulo y un círculo 🔺 + 🔵. Por otra parte, ¿qué ocurre cuando intentas sumar tres triángulos a cinco triángulos? 3🔺 + 5🔺? Acabarás con ocho triángulos 8🔺.

Sumar raíces cuadradas es muy parecido a esto. El resultado de sumar √2 + √3 sigue siendo √2 + √3. No puedes simplificarlo más sin resolver las raíces. Sin embargo, la situación es distinta cuando ambas raíces cuadradas tienen el mismo número bajo el símbolo de la raíz. Entonces podemos sumarlas como números normales (o triángulos). Por ejemplo, 3√2 + 5√2 es igual a 8√2. Lo mismo ocurre al restar raíces cuadradas. Veamos más ejemplos que ilustran esta propiedad de la raíz cuadrada:

• ¿Qué es 6√17 + 5√17? Respuesta: 6√17 + 5√17 = 11√17.

• ¿Qué es 4√7 - 7√7? Respuesta: 4√7 - 7√7 = -3√7.

• ¿Qué es 2√2 + 3√8? Respuesta: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, porque hemos simplificado √8 = √(4 × 2) = √4 × √2 = 2√2.

• ¿Cuánto es √45 - √20? Respuesta: √45 - √20 = 3√5 - 2√5 = √5, porque hemos simplificado √45 = √(9 × 5) = √9 × √5 = 3√5 y √20 = √(4 × 5) = √4 × √5 = 2√5.

• ¿Cuánto es 7√13 + 2√22? Respuesta: 7√13 + 2√22, no podemos simplificarlo más.

• ¿Qué es √3 - √18? Respuesta: √3 - √18 = √3 - 3√2, no podemos simplificarlo más, pero al menos hemos simplificado √18 = √(9 × 2) = √9 × √2 = 3√2.

Multiplicar raíces cuadradas y dividir raíces cuadradas

Ahora que sabes cómo sumar raíces cuadradas fácilemente, vayamos un paso más allá. ¿Qué te parece aprender cómo multiplicar raíces cuadradas y cómo dividir raíces cuadradas? ¡No te asustes! En realidad ya lo hemos hecho cuando hablamos de cómo simplificar raíces cuadradas. La multiplicación de raíces cuadradas se basa en la propiedad de la raíz cuadrada que hemos utilizado antes:

√x = x^(1/2)

¿Recuerdas cómo multiplicar números elevados a la misma potencia? A modo de recordatorio:

xⁿ × yⁿ = (x × y)ⁿ,

y, por tanto:

x^(1/2) × y^(1/2) = (x × y)^(1/2) ⟺ √x × √y = √(x × y).

A diferencia de la suma, puedes multiplicar cualquier raíz cuadrada. Recuerda que la multiplicación tiene propiedades conmutativas, lo que significa que el orden de los factores no altera el producto. Unos ejemplos aclararán esta cuestión:

• ¿Qué es √3 × √2? Respuesta: √3 × √2 = √6.

• ¿Qué es 2√5 × 5√3? Respuesta: 2√5 × 5√3 = 2 × 5 × √5 × √3 = 10√15, porque la multiplicación es conmutativa.

• ¿Qué es 2√6 × 3√3? Respuesta: 2√6 × 3√3 = 2 × 3 × √6 × √3 = 6√18 = 18√2, simplificamos √18 = √(9 × 2) = √9 × √2 = 3√2.

Dividir una raíz cuadrada es casi lo mismo, ya que:

x^(1/2) / y^(1/2) = (x / y)^(1/2) ⟺ √x / √y = √(x / y).

Basta con sustituir el signo de multiplicación por una división. Sin embargo, ¡la división no es un operador conmutativo! Tienes que calcular por separado los números que están delante de las raíces cuadradas y los números que están debajo de las raíces cuadradas. Como siempre, aquí tienes algunos ejemplos prácticos:

• ¿Cuánto es √15 / √3? Respuesta: √15 / √3 = √5;

• ¿Qué es 10√6 / 5√2? Respuesta: 10√6 / 5√2 = (10 / 5) × (√6 / √2) = 2√3;

• ¿Qué es 6√2 / 3√5? Respuesta: 6√2 / 3√5 = (6 / 3) × (√2 / √5) = 2√(2/5) = 2√(0.4), ahí pasamos de una fracción simple 2/5 a la fracción decimal 2/5 = 4/10 = 0.4.

Calcular la raíz cuadrada de números elevados a una potencia o la raíz cuadrada de fracciones puede ser confuso si no usas la calculadora de raíz cuadrada. Pero si quieres o necesitas hacerlo a mano, vamos a ver cómo sacar la raíz cuadrada de esos número fácilmente. Empecemos por sacar las raíces cuadradas de potencias. En ese caso, te resultará más fácil utilizar la forma alternativa de raíz cuadrada √x = x^(1/2). ¿Recuerdas la regla de las potencias? Si no es así, aquí tienes un rápido recordatorio rápido:

(xⁿ)^m = x^{(n × m)}

donde n y m son números reales cualesquiera. Ahora bien, si colocas 1/2 en lugar de m, obtendrás una fracción como exponente:

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2)

Y así es como se saca la raíz cuadrada de un número elevado a una potencia.

Si aún no estás seguro de cómo sacar raíces cuadradas de potencias, aquí tienes algunos ejemplos:

• Raíz cuadrada de 2⁴:

  √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4

• Raíz cuadrada de 5³:

  √(5³) = (5³)^(1/2) = 5^(3/2)

• Raíz cuadrada de 4⁵:

  √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32

Como puedes ver, a veces es imposible obtener un resultado bonito como el del primer ejemplo. Sin embargo, en el tercer ejemplo te mostramos un pequeño truco para expresar 4 como 2². A menudo, este método ayuda a simplificar ecuaciones y raíces más complicadas.

¿Qué pasa con las raíces cuadradas de fracciones? Echa un vistazo a la sección anterior, donde escribimos sobre la división de raíces cuadradas. Allí encontrarás la siguiente relación que debería explicarlo todo:

(x / y)^(1/2) ⟺ √x / √y = √(x / y)

donde x / y es una fracción. A continuación encontrarás algunos ejemplos de raíces cuadradas de una fracción:

• Raíz cuadrada de 4/9:

  √(4/9) = √4 / √9 = 2/3

• Raíz cuadrada de 1/100:

  √(1/100) = √1 / √100 = 1/10

• Raíz cuadrada de 1/5:

  √(1/5) = √1 / √5 = 1/√5 = √5/5

Dejar raíces en el denominador no es una buena costumbre, verás que nuestra calculadora de raíces cuadradas evita hacerlo. Por eso nos deshicimos de ella en el último ejemplo. Nos limitamos a multiplicar tanto el numerador como el denominador por el mismo número (siempre podemos hacerlo, ya que es lo mismo que multiplicar por 1), en este caso, por √5.

Aunque la calculadora de raíces cuadradas no tenga opción de representar funciones, por motivos obvios, estás son importantes. Las funciones nos ayudan a entender el comportamiento de ecuaciones (y operaciones como la raíz cuadrada) para cualquier número. Son de gran ayuda si quieres saber cómo calcular el interés compuesto o estimar el valor futuro de una renta vitalicia, o, en nuestro caso concreto, desarrollar la intuinción de cuánto más grande es la raíz cuadrada de 58 comparada con la raíz cuadrada de 11.

A continuación encontrarás la gráfica de la raíz cuadrada, formada por la mitad de una parábola. Chécala e intenta validar, por ejemplo, si la función raíz cuadrada de x = 9 es 3 y de x = 16 es 4 (como debería ser).

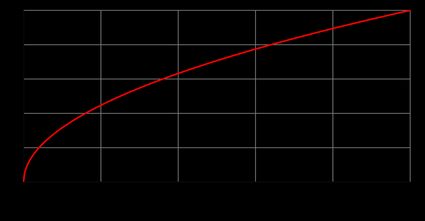
Volvamos a la función raíz cuadrada f(x) = √x y exploremos cuáles son sus propiedades básicas. Consideramos aquí sólo la parte positiva de f(x) (como puedes ver en la gráfica de la raíz cuadrada de arriba). Por tanto, la función raíz cuadrada:

• Es continua y creciente para todo x no negativo.

• Es diferenciable para todo x positivo (para más información, consulta la sección derivadas de la raíz cuadrada.

• Se aproxima al infinitio positivo a medida que x se crece, o se aproxima al infinito (lim √x → ∞ cuando x → ∞).

• Es un número real para todo x no negativo y un número complejo para todo x negativo.

La derivación de raíces cuadradas es un proceso que generalmente se hace más cómodamente a mano ya que las calculadoras númericas como esta calculadora de raíz cuadrada no pueden hacerlo por sí solas. Si es algo que realmente te interesa siempre puedes pedirnoslo e intentaremos crear una calculadora de raíces cuadradas que haga derivadas simbólicas, pero por ahora centrémonos en entender las derivadas y cómo hacerlas a mano.

Las derivadas de una función nos indican a qué velocidad cambia dicha función con su argumento. Uno de los ejemplos más sencillos en física es la posición de un objeto y su velocidad (la rapidez de cambio de posición). Digamos que la función x(t) describe cómo cambia la distancia del automóvil en movimiento desde un punto concreto con el tiempo t. ¿Sabes qué determina la rapidez del cambio en la distancia recorrida? La respuesta es ¡la velocidad del automóvil! Así que la derivada de la posición x(t) es la velocidad v(t) (la velocidad también puede depender del tiempo). Para denotar la derivada, solemos utilizar el apóstrofo v(t) = x'(t) o el símbolo de la derivada v(t) = dx(t)/dt.

La derivada de la función general f(x) no siempre es fácil de calcular. Sin embargo, en algunas circunstancias, si la función adopta una forma específica, tenemos algunas fórmulas. Por ejemplo, si

f(x) = xⁿ,

donde n es cualquier número real, la derivada es la siguiente:

f'(x) = n × x^(n-1).

Puede que no lo parezca, pero esto responde a la pregunta cuál es la derivada de una raíz cuadrada. ¿Recuerdas la forma alternativa (exponencial) de una raíz cuadrada? Vamos a recordártela:

√x = x^(1/2).

Puedes ver que en este caso, n = 1/2, por lo que la derivada de una raíz cuadrada es:

(√x)' = (x^(1/2))' = 1/2 × x^(-1/2) = 1/(2√x).

Como un número elevado a una potencia negativa es uno sobre ese número, la estimación de la derivada implicará fracciones. Tenemos una herramienta que puede ser esencial a la hora de sumar o restar fracciones con distintos denominadores. Se llama calculadora de MCM 🇺🇸, y te indica cómo hallar el mínimo común múltiplo.

La derivada de una raíz cuadrada es necesaria para obtener los coeficientes en la llamada expansión de Taylor. No queremos profundizar demasiado en los detalles, así que, brevemente, la serie de Taylor te permite aproximar diversas funciones con los polinomios, que son mucho más fáciles de calcular. Por ejemplo, la expansión de Taylor de √(1 + x) en torno al punto x = 0 viene dada por:

√(1 + x) = 1 + 1/2 × x - 1/8 × x² + 1/16 × x³ - 5/128 × x⁴ + ...,

que es válida para -1 ≤ x ≤ 1. Aunque la expresión anterior tiene un número infinito de términos, para obtener el valor aproximado, puedes utilizar sólo unos pocos primeros términos. ¡Vamos a probarlo! Con x = 0.5 y los cinco primeros términos, obtienes

√(1.5) = 1 + 1/2 × 0.5 - 1/8 × 0.25 + 1/16 × 0.125 - 5/128 × 0.0625,

√(1.5) ≈ 1.2241,

y el valor real, proporcionado por nuestra calculadora, es √(1.5) ≈ 1.2247. ¡Bastante cerca!

Hasta aquí muchas matemáticas y ecuaciones. Para los que seáis lo bastante persistentes, hemos preparado la siguiente sección, que explica cómo calcular la raíz cuadrada de un número negativo.

Nuestra calculadora de raíces cuadradas se queja y muestra un error si le preguntas cuál es la raíz cuadrada de un número negativo, tal y como probablemente te enseñaron de más chico.

Tiene sentido sentido porque al multiplicar un número por si mismo el resultado es positivo... ¿o no? En algún momento los matemáticos se hicieron está pregunta y decidieron ver qué pasaría si nos imaginamos un número que multiplicado por si mismo nos de un resultado negativo: el número i. Estos números se llaman imaginarios y tienen la forma:

x = a + b × i,

donde x es el número complejo con la parte real a y la parte imaginaria b. Lo que diferencia un número complejo de uno real es el número imaginario i. Aquí tienes algunos ejemplos de números complejos: 2 + 3i, 5i, 1,5 + 4i y 2. Quizá te sorprenda ver ahí 2, que es un número real. Sí, lo es, pero también es un número complejo con b = 0. Los números complejos son una generalización de los números reales

Hasta ahora, el número imaginario i probablemente siga siendo un misterio para ti. ¿Qué es? Bueno, aunque parezca raro, se define mediante la siguiente ecuación:

i = √(-1),

y eso es todo lo que necesitas para calcular la raíz cuadrada de cualquier número, sea positivo o no. Veamos algunos ejemplos de cómo sacar la raíz cuadrada de números imaginarios:

• Raíz cuadrada de -9: √(-9) = √(-1 × 9) = √(-1)√9 = 3i.
• Raíz cuadrada de -13: √(-13) = √(-1 × 13) = √(-1)√13 = i√13.
• Raíz cuadrada de -49: √(-49) = √(-1 × 49) = √(-1)√49 = 7i.

¿No es sencillo? Este problema no se plantea con la raíz cúbica, ya que puedes obtener el número negativo multiplicando tres números negativos idénticos (cosa que no puedes hacer con dos números negativos). Por ejemplo:

³√(-64) = ³√[(-4)×(-4)×(-4)] = -4.

Ahora ya sabes cómo se saca la raíz cuadrada de un número negativo y puedes enseñar a tus compañeros cómo sacar la raíz cuadrada de prácticamente cualquier número si lo necesitan. ¿No es maravilloso?