Calculadora de distancia

¿Alguna vez has querido calcular la distancia de un punto a otro, o la distancia entre dos ciudades? ¿Te has preguntado alguna vez cuál es la definición de distancia? Tenemos todas estas respuestas y más, incluida una explicación detallada de cómo calcular la distancia entre dos objetos cualesquiera en un espacio bidimensional. Como extra, tenemos un tema fascinante acerca de cómo percibimos distancias (por ejemplo, como diferencia porcentual) ¡Estamos seguros de que te encantará!

¿Prefieres ver a leer? Aprende todo lo que necesitas en 90 segundos con este vídeo que hemos hecho para ti:

Antes de entrar en cómo calcular distancias, probablemente deberíamos aclarar qué es distancia. El significado más común es el espacio unidimensional entre dos puntos. Esta definición es una forma de decir lo que casi todos pensamos intuitivamente sobre la distancia, pero no es la única forma en que podríamos hablar de distancia. En los apartados siguientes verás cómo el concepto de distancia puede ampliarse más allá de la longitud, en más de un sentido, que es el avance que hay detrás de la teoría de la relatividad de Einstein.

Si nos atenemos a la definición geométrica de distancia, aún tenemos que definir en qué tipo de espacio estamos trabajando. En la mayoría de los casos, probablemente estemos hablando de tres dimensiones o menos, ya que es todo lo que podemos imaginar sin que nos explote el cerebro. Para esta calculadora, nos centraremos únicamente en la distancia 2D (con la 1D incluida como caso especial). Si estás buscando la distancia 3D entre 2 puntos te sugerimos que utilices nuestra calculadora de distancia 3D 🇺🇸 hecha específicamente para ese fin.

Para hallar la distancia entre dos puntos, lo primero que necesitas son, por supuesto, dos puntos. Estos puntos se describen mediante sus coordenadas en el espacio. Para cada punto en un espacio 2D, necesitamos dos coordenadas que sean exclusivas de ese punto. Si quieres hallar la distancia entre dos puntos en el espacio 1D, puedes seguir usando esta calculadora simplemente estableciendo que una de las coordenadas sea la misma para ambos puntos. Como se trata de un caso muy especial, a partir de ahora solo hablaremos de distancia en dos dimensiones.

El siguiente paso, si quieres ser matemáticamente exacto y preciso, es definir el tipo de espacio en el que trabajas. No, espera, ¡no huyas! Es más fácil de lo que crees. Si no sabes en qué espacio estás trabajando o si ni siquiera sabías que hay más de un tipo de espacio, lo más probable es que estés trabajando en el espacio euclidiano. Ya que este es el espacio "por defecto" en el que realizamos casi todas las operaciones geométricas, y es en el que tenemos configurada la calculadora. Vamos a profundizar un poco más en el espacio euclídeo, ¿qué es, qué propiedades tiene y por qué es tan importante?

El espacio euclidiano o geometría euclidiana es lo que todos solemos pensar que es el espacio 2D antes de recibir una formación matemática profunda en cualquiera de estos aspectos. En el espacio euclídeo, la suma de los ángulos de un triángulo es igual a 180º y los cuadrados tienen todos sus ángulos iguales a 90º; siempre. Esto es algo que todos damos por supuesto, pero no es cierto en todos los espacios. Tampoco confundamos el espacio euclidiano con los espacios multidimensionales. El espacio euclidiano puede tener tantas dimensiones como quieras, siempre que haya un número finito de ellas, y sigan obedeciendo las reglas euclidianas.

No queremos aburrirte con definiciones matemáticas sobre qué es un espacio y qué hace que el espacio euclídeo sea único, ya que eso sería demasiado complicado de explicar en una simple calculadora de distancias. Sin embargo, podemos intentar darte algunos ejemplos de otros espacios que se utilizan habitualmente y que podrían ayudarte a comprender por qué el espacio euclídeo no es el único espacio. Además, esperemos que entiendas por qué no vamos a molestarnos en calcular distancias en otros espacios.

El primer ejemplo que te presentamos es un poco ofuscado, pero esperamos que puedas disculparnos, ya que somos físicos, por empezar con este tipo de espacio tan importante: El espacio de Minkowski. La razón por la que lo hemos seleccionado es porque es muy común en física, en concreto se utiliza en la teoría de la relatividad, la relatividad general e incluso en la teoría cuántica relativista de campos. Este espacio es muy similar al espacio euclidiano, pero difiere de él en una característica muy crucial: su producto punto, también llamado producto interno (no confundir con el producto cruz).

Tanto el espacio euclidiano como el de Minkowski son lo que los matemáticos llaman espacio plano. Esto significa que el espacio en sí tiene propiedades planas; por ejemplo, la distancia más corta entre dos puntos cualesquiera es siempre una línea recta entre ellos (consulta la calculadora de interpolación lineal 🇺🇸. Sin embargo, existen otros tipos de espacios matemáticos llamados espacios curvos, en los que el espacio es intrínsecamente curvo y la distancia más corta entre dos puntos no es una línea recta.

Este espacio curvo es difícil de imaginar en 3D, pero para 2D podemos imaginar que, en lugar de tener una superficie plana, tenemos un espacio 2D, por ejemplo, curvado en la forma de la superficie de una esfera. En este caso, ocurren cosas muy extrañas. La distancia más corta de un punto a otro no es una línea recta, porque cualquier línea en este espacio es curva debido a la curvatura intrínseca del espacio. Otra característica muy extraña de este espacio es que algunas rectas paralelas 🇺🇸 sí se encuentran en algún punto. Puedes intentar comprenderlo pensando en las llamadas líneas de longitud que dividen la Tierra en muchos husos horarios y se cruzan en los polos.

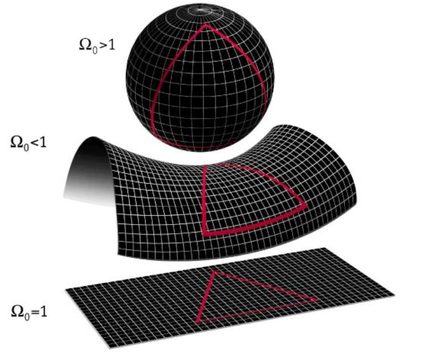
Es importante señalar que esto es conceptualmente MUY diferente de un cambio de coordenadas. Cuando tomamos las coordenadas estándar $x, y, z$ y las convertimos en coordenadas polares, cilíndricas o incluso esféricas, seguiremos estando en el espacio euclidiano. Cuando hablamos de espacio curvo, estamos hablando de un espacio muy diferente en cuanto a sus propiedades intrínsecas. En coordenadas esféricas, puedes seguir teniendo una línea recta y la distancia se sigue midiendo en línea recta, incluso aunque eso sea muy difícil de expresar en números.

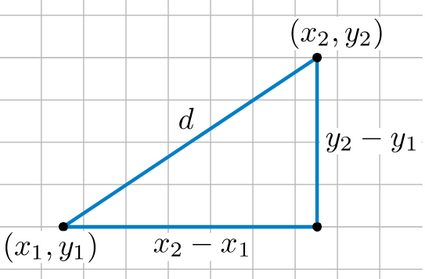
Volviendo al espacio euclídeo, ahora podemos presentarte la fórmula de la distancia que te prometimos al principio. La fórmula de la distancia es

que se relaciona con el Teorema de Pitágoras, que afirma que $a^2+b^2=c^2$. Aquí, $a$ y $b$ son los catetos de un triángulo rectángulo y $c$ es la hipotenusa. Supongamos que dos puntos, $(x_1, y_1)$ y $(x_2, y_2)$, son coordenadas de los extremos de la hipotenusa. Entonces $(x_2 - x_1)^2$ en la ecuación de la distancia corresponde a $a^2$ y $(y_2 - y_1)^2$ corresponde a $b^2$. Puesto que $c = \sqrt{a^2 + b^2}$, puedes ver por qué esto no es más que una extensión del teorema de Pitágoras.

La fórmula de distancia que acabamos de ver es la fórmula estándar de la distancia euclídea, pero si lo piensas un poco, puede parecer un poco limitada. A menudo no queremos hallar solo la distancia entre dos puntos. Algunas veces queremos calcular la distancia de un punto a una recta o a una circunferencia. En estos casos, primero tenemos que definir es qué punto de esta recta o circunferencia vamos a utilizar para el cálculo de la distancia, y luego utilizar la fórmula de la distancia que hemos visto arriba.

Aquí es cuando el concepto de recta perpendicular 🇺🇸 resulta crucial. La distancia entre un punto y un objeto continuo se define mediante la perpendicularidad. Desde un punto de vista geométrico, el primer paso para medir la distancia de un punto a otro, es crear una línea recta entre ambos puntos, y luego medir la longitud de ese segmento. Cuando medimos la distancia de un punto a una recta, la pregunta se convierte en "¿Cuál de las muchas rectas posibles debo trazar?". En este caso la respuesta es la recta que pasa por el punto y que es perpendicular a la primera recta. Esta distancia será cero en el caso en que el punto sea una parte de la recta. Para estos casos 1D, solo podemos considerar la distancia entre puntos, ya que la recta representa todo el espacio 1D.

Esto impone restricciones a la forma de calcular distancias en algunos casos geométricos interesantes. Por ejemplo, podríamos redefinir el concepto de altura de un triángulo para que fuera simplemente la distancia de un vértice al lado opuesto del triángulo. En este caso, el área del triángulo también se redefine en términos de distancia, ya que el área es una función de la altura del triángulo.

Veamos un par de ejemplos en el espacio 2D. Para calcular la distancia entre un punto y una recta podríamos ir paso a paso (calcular el segmento perpendicular a la recta desde la recta hasta el punto y luego calcular su longitud) o podríamos simplemente utilizar esta ecuación:

donde la línea viene dada por $Ax+By+C = 0$ y el punto viene definido por $(x_1, y_1)$.

El único problema aquí es que una recta viene dada generalmente por $y=mx+b$, por lo que tendríamos que convertir esta ecuación a la forma mostrada anteriormente:

por lo que podemos ver que $A=m$, $B=-1$ y $C=b$. Esto deja la ecuación anterior con los siguientes valores:

Para la distancia entre 2 rectas, basta con calcular la longitud del segmento que va de una a otra y es perpendicular a ambas. Una vez más, existe una fórmula para ayudarnos:

si las rectas son $A_1x+B_1y+C_1=0$ y $A_2x+B_2y+C_2=0$. También podemos convertir a la forma pendiente-intersección y obtener:

para las rectas $y=m_1x+b_1$ y $y=m_2x+b_2$.

Observa que ambas rectas deben ser paralelas, ya que de lo contrario se tocarían en algún punto y su distancia sería $d=0$. Esa es la razón por la que las fórmulas omiten la mayoría de los subíndices, puesto que para las rectas paralelas: $A_1=A_2=A$ y $B_1=B_2=B$ mientras que en la forma pendiente-intersección las rectas paralelas son aquellas para las que $m_1=m_2=m$.

Como hemos dicho antes, distancia puede significar muchas cosas, por eso te hemos proporcionado diferentes opciones en esta calculadora. Puedes calcular la distancia entre un punto y una recta, la distancia entre dos rectas (siempre tienen que ser paralelas), o la distancia entre puntos en el espacio. Cuando se trata de calcular las distancias entre dos puntos, tienes la opción de hacerlo en 1, 2, 3 o 4 dimensiones. Está bien, lo sabemos, 4 dimensiones suena aterrador, pero no es necesario que utilices esa opción. Y siempre puedes aprender más sobre ello leyendo algunos recursos interesantes y jugando con la calculadora. Te prometemos que no romperá Internet ni el universo.

También hemos añadido la posibilidad de que definas 3 puntos diferentes en el espacio, a partir de los cuales obtendrás los 3 pares de distancias entre ellos, así que, si tienes más de dos puntos, esto te ahorrará tiempo. El número de dimensiones con las que trabajes determinará el número de coordenadas que describen un punto, por eso, a medida que aumentes el número de dimensiones, la calculadora te pedirá más valores.

Aunque el uso de la calculadora es muy sencillo, hemos decidido incluir una solución paso a paso. Así podrás familiarizarte con la fórmula de la distancia y cómo utilizarla (como si estuviéramos en los años 50 e Internet aún no existiera). Veamos ahora un ejemplo práctico: Cómo hallar la distancia entre dos puntos en 2D.

Supongamos que tienes dos coordenadas, $(3, 5)$ y $(9, 15)$, y quieres calcular la distancia entre puntos. Para calcular la distancia en 2-D entre estos dos puntos, sigue estos pasos:

1. Introduce los valores en la fórmula $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
2. En la fórmula, resta los valores dentro del paréntesis.
3. Eleva al cuadrado las dos cantidades entre paréntesis.
4. Suma los resultados.
5. Saca la raíz cuadrada.
6. Usa la calculadora de distancias para comprobar tus resultados.

Calculando el ejemplo a mano, obtienes:

que es aproximadamente $11.66$. Ten en cuenta que, al sacar la raíz cuadrada, obtendrás un resultado positivo y otro negativo, pero como se trata de la distancia, solo te interesa el resultado positivo. La calculadora realizará este cálculo paso a paso para darte el resultado en formato exacto y aproximado.

Veamos una de los usos de la calculadora de distancias. Supongamos que viajas entre las ciudades A y B, y que la única parada es en la ciudad C. La ruta de A a B es perpendicular a la ruta de B a C. Podemos determinar la distancia de A a B, y luego, conociendo el precio de la gasolina, determinar el coste del combustible, el combustible utilizado y el coste por persona durante el viaje. La calculadora de gasolina, que puedes encontrar en nuestro sitio, puede facilitarte esa tarea.

La dificultad aquí es calcular con precisión las distancias entre ciudades. Una línea recta (como la que utilizamos en esta calculadora) puede ser una buena aproximación, pero puede fallar bastante si la carretera que tomas no es directa, sino que toma algún desvío, quizá para evitar montañas o para pasar por otra ciudad. En ese caso, usa Google Maps o cualquier otra herramienta que calcule la distancia a lo largo de un camino y no solo la distancia de un punto a otro en línea recta.

Nuestra calculadora puede dar medidas y predicciones para distancias entre objetos, no la longitud de un camino. Teniendo esto en cuenta, sigue habiendo múltiples escenarios en los que realmente te puede interesar conocer la distancia entre objetos, independientemente del camino que tengas que recorrer. Un ejemplo de ello es la distancia entre objetos astronómicos.

Cuando consideramos una distancia dentro de nuestra Tierra, es difícil ir lejos sin tropezar con algunos problemas, desde la curvatura intrínseca de este espacio (debido a que la curvatura de la Tierra es distinta de cero) hasta la distancia máxima entre dos puntos de la Tierra. Por ello, y también porque hay todo un universo más allá de nuestra Tierra, las distancias en el universo son de gran interés para muchas personas. Como no disponemos de medios adecuados para realizar viajes interplanetarios, y mucho menos viajes interestelares, centrémonos por ahora en la distancia euclidiana a algunos objetos celestes. Por ejemplo, la distancia de la Tierra al Sol, o la distancia de la Tierra a la Luna.

Estas distancias están más allá de lo imaginable para nuestros cerebros. Nos cuesta comprender el tamaño de nuestro planeta, por no hablar del vasto e infinito universo. Esto es tan difícil que necesitamos utilizar la notación científica o los años luz, como unidad de distancia para longitudes tan grandes. Los viajes más largos que puedes hacer en la Tierra son de apenas un par de miles de kilómetros, mientras que la distancia de la Tierra a la Luna, el objeto astronómico más cercano a nosotros, es de 384 000 km. Además, la distancia a nuestra estrella más cercana, que es la distancia de la Tierra al Sol, es de 150 000 000 km o algo más de 8 minutos luz.

Si comparamos estas distancias con la distancia a nuestra segunda estrella más cercana (Alfa Centauri), que es de 4 años luz, de repente empiezan a parecer mucho más pequeñas. Si queremos hacer una comparación aún más ridícula, podemos pensar en un vuelo de Madrid (España) a Lima (Perú), que suele durar aproximadamente 12 h y tiene 9500 km, y compararlo con el tamaño del universo observable, que es de unos 46 600 000 000 de años luz****

Aquí, sin darnos cuenta, hemos desvelado un punto fascinante, y es que no medimos las distancias en longitud, sino en tiempo. Así, ampliamos la noción de distancia más allá de su sentido geométrico. Exploraremos esta posibilidad en la próxima sección, cuando hablemos de la importancia y utilidad de la distancia más allá del sentido puramente geométrico. Se trata de un camino muy interesante y se inspira sobre todo en la necesidad filosófica de ampliar todo concepto para que tenga un significado universal, así como también lo requiere la teoría física que todos conocemos, al hablar de permutaciones del espacio y el tiempo, o de cualquier otra variable que pueda medirse.

Normalmente, el concepto de distancia se refiere a la distancia geométrica euclidiana y está vinculado a la longitud. Sin embargo, puedes ampliar la definición de distancia para que signifique solo la diferencia entre dos cosas, y entonces se abre un mundo de posibilidades. De repente se puede decidir cuál es la mejor forma de medir la distancia entre dos cosas y ponerla en términos de la cantidad más útil. Un paso muy sencillo es pensar en la distancia entre dos números, que no es más que la diferencia 1D entre estos números. Para obtenerla, simplemente restamos uno del otro y el resultado sería la diferencia, es decir, la distancia.

Podríamos saltar de esta distancia numérica a, por ejemplo, la diferencia o distancia en términos de diferencia porcentual, que en algunos casos podría proporcionar una mejor forma de comparación. Esto no deja de ser un nivel de abstracción en el que simplemente eliminamos las unidades de medida. Pero, ¿y si utilizáramos unidades totalmente distintas?

Ampliando el concepto de distancia para que signifique algo más cercano a la diferencia, podemos calcular la diferencia entre dos temperaturas, u otra cantidad similar, como la presión. Pero no hace falta que lleguemos a extremos, veamos cómo dos puntos pueden estar separados por una distancia diferente, dependiendo de las suposiciones que hagamos. Volviendo al ejemplo de la distancia de manejo, podríamos medir la distancia del trayecto en tiempo, en lugar de en longitud. En este caso, necesitamos una suposición para permitir dicha traslación; a saber, el medio de transporte.

Hay una gran diferencia entre el tiempo que se tarda en recorrer 10 km en avión y el que se tarda en automóvil. A veces, sin embargo, la suposición es clara y está implícitamente acordada, como cuando medimos la distancia de un rayo utilizando tiempo, para luego convertirlo en longitud. Esto plantea un punto interesante: que el factor de conversión entre distancias en tiempo y longitud es lo que llamamos “rapidez” o “velocidad” (recuerda que no son exactamente lo mismo). A decir verdad, esta velocidad no tiene por qué ser constante, como ejemplifican los movimientos acelerados, como el de una caída libre bajo la fuerza gravitatoria, el que relaciona el tiempo de frenado y la distancia de frenado mediante la fuerza de frenado y la resistencia o, en casos muy extremos, mediante la fuerza de un accidente de automóvil.

Otro lugar donde puedes encontrar unidades extrañas de distancia es en la física del estado sólido, donde la distancia que recorre una partícula en el interior de un material suele expresarse como un promedio de interacciones o colisiones. Esta distancia se relaciona con la longitud mediante el camino libre medio, que es la distancia media (en longitud) que recorre una partícula entre interacciones. Si queremos ponernos aún más exóticos, podemos pensar en la distancia del valor actual al valor futuro de algo (como un automóvil).

Sin embargo, no queremos hacer explotar el cerebro de nadie, así que, por favor, no reflexiones demasiado sobre esto. Simplemente, coge esta calculadora y úsala para la distancia basada en la longitud en un espacio 2D. Siempre puedes volver a esta visión filosófica de las distancias si alguna vez te aburres.

Para hallar la distancia entre dos puntos utilizaremos la fórmula de la distancia: √[(x₂ - x₁)² + (y₂ - y₁)²]:

1. Obtén las coordenadas de ambos puntos en el espacio.
2. Resta las coordenadas x de un punto del otro, lo mismo para las componentes y.
3. Eleva al cuadrado ambos resultados por separado.
4. Suma los valores obtenidos en el paso anterior.
5. Halla la raíz cuadrada del resultado anterior.

Si te parece demasiado esfuerzo, puedes utilizar simplemente la calculadora de distancia de Omni

La distancia no es un vector. La distancia entre puntos es una cantidad escalar, es decir, solo está definida por su valor. Sin embargo, el desplazamiento sí es un vector con valor, dirección y sentido. Así, la distancia de A a B es la misma que de B a A, pero el desplazamiento es distinto según su orden.

“Klick” es un término empleado para referirse al kilómetro. Se escribe con "k" (klick), ya que deriva de la palabra kilómetro. Se utiliza habitualmente en el ejército y entre los motociclistas.

La fórmula de distancia es √[(x₂ - x₁)² + (y₂ - y₁)²]. Esto funciona para dos puntos cualesquiera en el espacio 2D, con coordenadas (x₁, y₁) para el primer punto y (x₂, y₂) para el segundo. Puedes memorizarlo fácilmente si observas que se trata del teorema de Pitágoras y que la distancia es la hipotenusa, y las longitudes de los catetos son la diferencia entre las componentes x e y de los puntos.

La distancia de un vector es su magnitud. Si conoces sus componentes:

1. Toma cada una de las componentes del vector y elévalas al cuadrado.
2. Súmalas.
3. Halla la raíz cuadrada del resultado anterior.
4. ¡Disfruta del buen trabajo!

Si conoces su representación en coordenadas polares, será un número y un ángulo. Ese número es la magnitud del vector, que es su distancia.

La unidad SI de distancia es el metro, abreviado como “m”. Un metro equivale aproximadamente a 3.28 pies. Otras unidades comunes del Sistema Internacional de unidades son el centímetro (una centésima parte de un metro, o 0.39 pulgadas) y el kilómetro (mil metros o 0.62 millas), entre otras.

La distancia de A a B es la longitud de la recta que va de A a B. La distancia de B a A es la misma que la distancia de A a B porque la distancia es un escalar.

La distancia es una medida del espacio unidimensional. La distancia entre dos puntos es la longitud más corta del espacio unidimensional entre ellos. Si divides la distancia por el tiempo, obtendrás la velocidad, que tiene dimensiones de espacio por tiempo.

Un año-luz es una medida de distancia. Son 9.461×10¹² kilómetros o 5.879×10¹² millas, que es la distancia recorrida por un rayo de luz en el vacío a lo largo de un año.

La velocidad y el tiempo de desplazamiento de un objeto te permiten calcular la distancia:

1. Asegúrate de que la velocidad y el tiempo tienen unidades compatibles (metros por segundo y segundos, kilómetros por hora y horas, etc...).
2. Si no lo son, conviértelas a las unidades necesarias.
3. Multiplica la velocidad por el tiempo.
4. El resultado debería ser la distancia recorrida en las unidades de longitud que utilizaba tu velocidad.