Calculadoras de triángulos 45-45-90

Esta calculadora de triángulos 45-45-90 está hecha para resolver este triángulo rectángulo especial. Averigua cuáles son los lados, la hipotenusa, el área, y el perímetro, y aprende sobre las fórmulas y proporciones del triángulo 45-45-90. También hablaremos de las reglas del triángulo 45-45-90 que tienen más probabilidad de aparecer en tus tareas escolares. Nunca más te preguntarás cómo resolver un triángulo 45-45-90.

Si quieres saber más sobre otros triángulos rectángulos populares, consulta esta calculadora de triángulos 30-60-90 y la calculadora de triángulos rectángulos especiales.

¿Necesitas fórmulas para el triángulo 45-45-90? ¡Estás en el sitio adecuado! Si el cateto del triángulo es igual a a, entonces:

• el segundo cateto también es igual a a;
• la hipotenusa es a√2;
• el área es igual a a²/2; y
• el perímetro es igual a a(2 + √2).

De acuerdo, estas fórmulas de triángulos 45-45-90 parecen fáciles, pero ¿de dónde salen? Hay un par de métodos para demostrarlas, los más populares son:

1. Usando el teorema de Pitágoras

• Dado que ya conoces la longitud de uno de los catetos (a), también sabes la longitud del otro, ya que ambos son iguales.

• Calcula la hipotenusa usando el teorema de Pitágoras: tenemos a² + b² = c² y a = b, así que

  a² + a² = c²

  lo que da

  c = √(2a²) = a√2

2. Usando las propiedades de los cuadrados

¿Has notado que el triángulo 45-45-90 es la mitad de un cuadrado dividido a lo largo de su diagonal?

• De nuevo, sabemos que ambos catetos son iguales a a.
• Como probablemente recuerdes, la diagonal del cuadrado es igual a lado por raíz cuadrada de 2, es decir a√2. En nuestro caso, esta diagonal es igual a la hipotenusa. ¿Rápido, no?

3. Usando trigonometría

Si tienes conocimientos de trigonometría, podrías aplicar las propiedades del seno y el coseno. Para este ángulo especial de 45°, ambos son iguales a √2/2. Así que
a/c = √2/2 entonces c = a√2

Para hallar el área del triángulo, utiliza la fórmula básica del área del triángulo, que es área = base × altura / 2. En nuestro caso, un cateto es la base y el otro es la altura, ya que hay un ángulo recto entre ellos. Por lo tanto, el área de un triángulo 45-45-90 es:

área = a²/2

Para calcular el perímetro, basta con sumar todos los lados del triángulo 45-45-90:

Perímetro = a + b + c = a + a + a√2 = a(2 + √2)

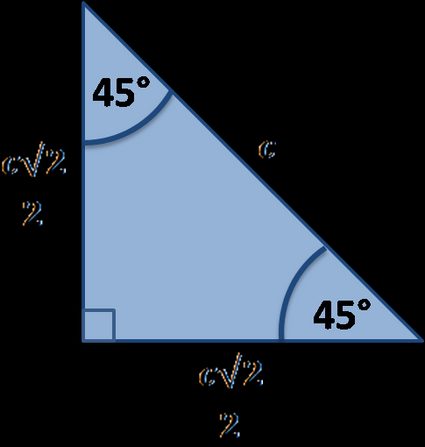
Los catetos de dicho triángulo son iguales, por lo que la hipotenusa se calcula fácilmente a partir de la ecuación c = a√2. Por otro lado, si se da el valor de la hipotenusa, la longitud del lado será igual a a = c√2/2.

La regla más importante es que este triángulo tiene un ángulo recto y otros dos ángulos iguales a 45°. Esto implica que dos lados —los catetos— tienen la misma longitud, y puedes calcular la hipotenusa fácilmente. Otras propiedades interesantes de los triángulos 45-45-90 son:

• es el único triángulo rectángulo que también es un triángulo isósceles;
• De todos los triángulos rectángulos, es el que tiene la menor proporción entre la hipotenusa y la suma de los catetos; y
• De todos los triángulos rectángulos, es el que tiene la mayor proporción entre altitud y la suma de los catetos (tomando como base a la hipotenusa).

En un triángulo 45-45-90, las proporciones son las siguientes:

• 1 : 1 : 2 para los ángulos (45° : 45° : 90°); y
• 1 : 1 : √2 para los lados (a : a : a√2).

Echa un vistazo a este ejemplo real para entender las reglas del triángulo 45-45-90.

Supongamos que queremos resolver el triángulo isósceles del juego de escuadras anterior.

1. Escribe el valor conocido. En nuestro caso, lo más sencillo es introducir la longitud del cateto horizontal, el cual se puede medir con la escala. Su longitud habitual es de 20 centímetros, así que teclea ese valor en la casilla a o b.
2. Inmediatamente, la calculadora de triángulos 45-45-90 mostrará el resto de los parámetros.

Ahora ya sabes:

• longitud de la hipotenusa = 20 cm × √2 = 28.3 cm;
• área = 20 cm × 20 cm / 2 = 200 cm²; y
• perímetro = 20 cm + 20 cm + 20 cm × √2 = 68.3 cm.

Recuerda que puedes cambiar las unidades simplemente haciendo clic en el nombre de la unidad. Además, no olvides que nuestra calculadora de triángulos 45-45-90 es una herramienta flexible: si solo conoces el área, la hipotenusa o incluso el perímetro, también puede calcular el resto de los parámetros. ¡Genial! 😉