Última actualización: 07 de Jul. de 2024

Calculadora de triángulos rectángulos especiales

Q: ¿Cuáles son las fórmulas de un triángulo 45-45-90?

Un triángulo 45-45-90 tiene las siguientes fórmulas, donde x es la longitud de cualquiera de los lados iguales: Hipotenusa = x√2 ; Área = x²/2 ; Perímetro = x(2+√2) .

Q: ¿Es 3, 4 y 5 un triplete pitagórico?

**Sí. Los números enteros a = 3 , b = 4 y c = 5 forman un triplete pitagórico, ya que a² + b² = c² , y un triángulo de lados abc es un triángulo rectángulo especial.

Creada por Hanna Pamuła, doctorado/a

Revisada por Bogna Szyk y Adena Benn

Adena Benn

LinkedInWebsite

Adena Benn is an Information Technology teacher with a degree in Computer Science. She has been teaching high schoolers since 1996 and loves everything computers. She loves problem-solving, so creating calculators to solve real-world problems is her idea of fun. She writes children's stories, is a seamstress, and is an avid reader. In her spare time, she travels and enjoys nature. See full profile

Check our editorial policy

Traducida por Luis Hoyos

Luis Hoyos

Luis Hoyos is a fresh graduate Mechanical Engineer with thermodynamics and fluids mechanics expertise. He's interested in learning new things and applying them to real-life problems. Luis also likes to build tools that make repetitive and boring tasks a breeze, like calculators (surprise?). When he's not creating calculators, he's in the process of building the size of the tissue attached to his bones, aka bodybuilding. He also loves being with his little cat and seeing her do crazy things. See full profile

Check our editorial policy

¡Nuevo!

Índice general

Triángulos rectángulos especiales 30 60 90 Triángulos rectángulos especiales 45 45 90 Otros triángulos rectángulos especiales Fórmulas de los triángulos rectángulos especiales Reglas especiales del triángulo rectángulo Calculadora especial triángulo rectángulo: un ejemplo Preguntas frecuentes

Esta calculadora especial de triángulos rectángulos te ayudará a resolver las medidas del triángulo elegido en un abrir y cerrar de ojos. Selecciona el triángulo que necesites e introduce los valores dados: el resto de parámetros se calcularán automáticamente.

Los triángulos rectángulos especiales son triángulos rectángulos para los que existen fórmulas sencillas. Esto permite cálculos rápidos, por lo que no necesitas utilizar el teorema de Pitágoras o algún método avanzado. Desplázate hacia abajo para leer más sobre las fórmulas y reglas de los triángulos rectángulos especiales.

Triángulos rectángulos especiales 30 60 90

El triángulo rectángulo especial $30\degree$ $60\degree$ $90\degree$ es uno de los triángulos rectángulos más populares. Sus propiedades son únicas porque es la mitad del triángulo equilátero.

Triángulo rectángulo especial: 30-60-90.

Si quieres saber más sobre esta forma especial, consulta nuestra calculadora de triángulos 30° 60° 90°.

Triángulos rectángulos especiales 45 45 90

Otro famoso triángulo rectángulo especial es el $45\degree$ $45\degree$ $90\degree$ triángulo. Es el único triángulo rectángulo posible que también es un triángulo isósceles. Además, es la forma que se crea cuando cortamos el cuadrado por la diagonal:

Triángulo rectángulo especial: 45-45-90 con una longitud de cateto determinada.

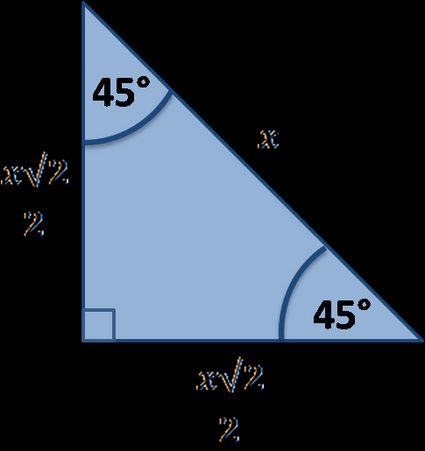
Triángulo rectángulo especial: 45-45-90 con una longitud de hipotenusa dada.

¿Tienes curiosidad por conocer las propiedades de este triángulo? Consulta nuestra calculadora de triángulo 45-45-90.

Otros triángulos rectángulos especiales

Existen muchos triángulos rectángulos especiales, a continuación encontrarás los implementados en nuestra herramienta:

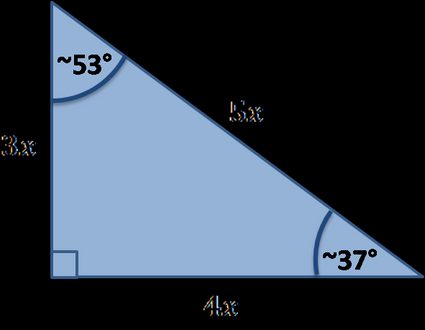
Triángulo rectángulo especial: 3x-4x-5x.

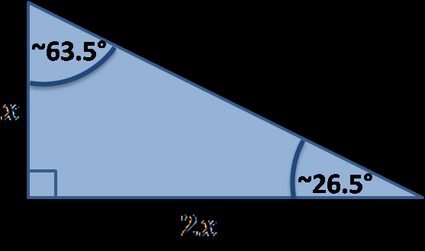
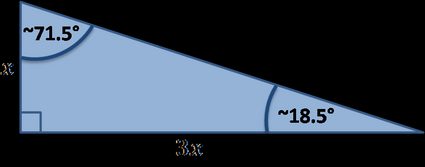
Fórmulas de los triángulos rectángulos especiales

Triángulo rectángulo de lados a, b, c y ángulos α, β.

Si buscas las fórmulas de los triángulos rectángulos especiales, estás en el lugar adecuado. Fíjate en la tabla que aparece a continuación; ¡todo debería estar claro! En esta tabla encontrarás las fórmulas para la relación entre los ángulos, catetos, hipotenusa, área y perímetro de los triángulos rectángulos especiales:

Triangulo rectángulo especial	$a$ (cateto corto)	$b$ (cateto largo)	$c$ (hipotenusa)	Área	Perímetro	Ángulo $\alpha$	Ángulo $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\sim26.5\degree$	$\sim63.5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\sim18.5\degree$	$\sim71.5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\sim37\degree$	$\sim53\degree$

Reglas especiales del triángulo rectángulo

Los triángulos rectángulos especiales son los triángulos que tienen algunas características específicas que facilitan los cálculos. Por supuesto, la regla más importante de los triángulos rectángulos especiales es que deben tener un ángulo recto además de esa característica extra. En general, los triángulos rectángulos especiales pueden dividirse en dos grupos:

Triángulos rectángulos basados en ángulos; por ejemplo, los triángulos $30\degree$ - $60\degree$ - $90\degree$ y $45\degree$ - $45\degree$ - $90\degree$ .
Triángulos rectángulos basados en los lados; figuras cuyas longitudes de los lados se rigen por una regla específica, por ejemplo:
- Lados con longitudes enteras llamados tripletes pitagóricos:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ ..
- Lados con longitudes enteras pero casi isósceles:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ ..
- Triángulo rectángulo cuyos lados siguen una progresión geométrica (triángulo de Kepler). Está formado por tres lados cuadrados. Sus áreas están en progresión geométrica, según la proporción áurea. Para más información sobre esta proporción especial, visita nuestra calculadora de la proporción áurea.

Hay muchas reglas y opciones diferentes por las que podemos elegir el triángulo y llamarlo especial. En nuestra calculadora de triángulos rectángulos especiales, implementamos cinco triángulos elegidos: dos basados en ángulos y tres basados en lados.

Calculadora especial triángulo rectángulo: un ejemplo

Veamos un ejemplo: queremos hallar la longitud de la hipotenusa de un triángulo rectángulo si la longitud de un cateto es $5$ cm y un ángulo es $45\degree$ .

Elige el tipo adecuado de triángulo rectángulo especial. En nuestro caso, es el triángulo $45\degree$ - $45\degree$ - $90\degree$ .
Escribe el valor dado. Sabemos que el lado es igual a $5$ en, así que escribimos ese valor en la casilla a o b; no importa dónde porque es un triángulo isósceles.
¡Vaya! ¡La calculadora especial de triángulos rectángulos ha resuelto las medidas de tu triángulo! Ahora ya lo sabemos:
- El segundo cateto $b$ es igual a $5\ \mathrm{cm}$ ;
- Hipotenusa $c$ es $7.07\ \mathrm{cm}$ ;
- El perímetro es igual a $17.07\ \mathrm{cm}$ ; y
- El área de nuestro triángulo especial es $12.5\ \mathrm{cm^2}$ .

No esperes más. ¡Pruébalo tú mismo!

Preguntas frecuentes

¿Cuáles son las fórmulas de un triángulo 45-45-90?

Un triángulo 45-45-90 tiene las siguientes fórmulas, donde x es la longitud de cualquiera de los lados iguales:

Hipotenusa = x√2;
Área = x²/2;
Perímetro = x(2+√2).

¿Cómo resuelvo un triángulo rectángulo especial 30 60 90?

Para resolver un triángulo rectángulo especial de 30° 60° 90°, sigue estos pasos:

Halla la longitud del cateto más corto. Lo llamaremos x.
El cateto más largo será igual a x√3.
Su hipotenusa será igual a 2x.
El área es A = x²√3/2.
Por último, el perímetro es P = x(3 + √3).

¿Cuáles son los dos triángulos especiales en trigonometría?

Los triángulos 30° 60° 90° y 45° 45° 90° (o triángulo rectángulo isósceles) son los dos triángulos especiales de la trigonometría. Aunque hay más de dos triángulos rectángulos especiales diferentes, éstos son los más rápidos de reconocer y con los que resulta más fácil trabajar. Un ejemplo de triángulo rectángulo especial no basado en ángulos es un triángulo rectángulo cuyos lados forman una terna pitagórica.

¿Es 3, 4 y 5 un triplete pitagórico?

**Sí. Los números enteros a = 3, b = 4 y c = 5 forman un triplete pitagórico, ya que a² + b² = c², y un triángulo de lados abc es un triángulo rectángulo especial.