Last updated: Jun 08, 2024

Carrying Capacity Calculator

Q: What is the carrying capacity in biology?

The carrying capacity is the maximum number of individuals sustainable by a specific environment . This quantity corresponds to a plateau in the population reached after a period of growth or shrinkage. In the logistic model, only a few factors affect the carrying capacity: The intrinsic growth rate r ; and The rate of change of the population at a given time.

Q: What is the carrying capacity of Earth for a human population?

Between 7 and 11 billion. Scientists don't know the limit to humanity's growth precisely, but they agree that it is close to the current number of individuals hosted on the Planet. If we've already passed Earth's carrying capacity, we will face a phase of rapid shrinking of the population; otherwise, we will meet a plateau (expected for the second half of the century).

Q: What is the carrying capacity of a population of 100 individuals growing at a rate of 25 individuals per year, and with an intrinsic growth rate r=0.27?

1,350 individuals. To calculate the carrying capacity, first, identify the given data: r = 0.27 ; N = 100 ; and C p = 25 . This combination identifies a particular moment in the growth of a population. The rate of change is rather high, meaning that we are far from the carrying capacity. Let's use the formula to calculate K : K = N/(1 - (C p /r × N)) = 100 × 1/(1 − (25/(0.27 × 100)) = 1,350 .

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Łucja Zaborowska, MD, PhD candidate and Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

How does a population grow? – the logistic model Definition of carrying capacity in biology How do I calculate the carrying capacity?Some practical examples of carrying capacity: rabbits and bacteria Did humanity pass the carrying capacity of Earth?FAQs

Math underlines the dynamics of populations: learn one of the fundamental laws of ecology with our carrying capacity calculator.

Keep reading to learn:

Why can we find math in biology?
What are the laws of population growth?
What is the carrying capacity?
How to calculate the carrying capacity from the logistic equation.
Some examples of carrying capacity.

Plus, much more. Explore the point of contact between math and biology with Omni!

How does a population grow? – the logistic model

To enter this topic, we need to introduce a friend: Thomas Robert Malthus. At the end of the 18^th century, he single-handedly revolutionized the field of mathematical biology by finding and modeling the correlation between population growth and exponential functions.

The connection formally made it possible to describe the growth of a population with a dynamical system.

🔎 A dynamical system, in science, is a set of equations describing the trajectory of a point in a specific space. Often, dynamical systems use relatively simple equations with an emerging complexity that can lead to the rise of chaotic phenomena.

In particular, the logistic equation governs the number of individuals in a population. Please take a look at it: it is surprisingly simple!

\frac{\mathrm{d}N}{\mathrm{d}t} = r\times N \times \left(1-\frac{N}{K}\right)

We could write a couple of books about this equation, but we will keep it short. Let's identify the elements of the logistic equation:

$N$ is the number of individuals at a given time;
$r$ is the rate of change per individual; and
$K$ is the carrying capacity.

The logistic equation is a differential equation: the left-hand side is a derivative, particularly the derivative of the number of individuals with respect to time. In other words, this derivative is the rate of increase of the population. If you think of the curve describing the population over time, the equation above is nothing but its slope.

🔎 Mathematical corner! The expression $\tfrac{\mathrm{d}N}{\mathrm{d}t}$ is a derivative. We read it as "derivative of $N$ with respect to $t$ " and is only a notation, where $\mathrm{d}N$ and $\mathrm{d}t$ are infinitely small intervals of the relative quantities.

In the graph below, you can appreciate the behavior of that function.

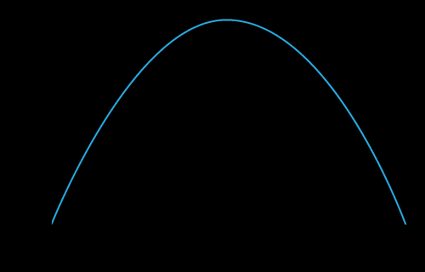
Note that the population starts and ends changing at an extremely low pace, while it has a maximum between the beginning and when it reaches the carrying capacity.

You can find it interesting to see how the population effectively changes with time: that's why we solved the differential equation for you (it is slightly tricky and out of scope):

N = \frac{1}{(1 + ((K - 1)\times \mathrm{e}^{-r\times t}))}

We assumed that the initial population is $N_0 =1$ , but this doesn't make much of a difference in this context. Now we can plot it!

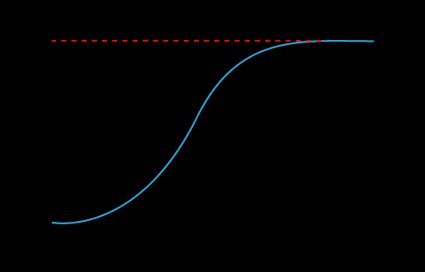
Logistic function — A population grows following the logistic curve. The dashed red line indicates the carrying capacity.

As you can see, the population (on the vertical axis) starts growing slowly, then accelerates: it makes sense since there are more individuals capable of reproducing.

However, the curve slows down and reaches a plateau: the population meets the carrying capacity. We will talk in detail about the carrying capacity in the next section. For now, we need to focus for a moment on $r$ , the rate of change per individual. The value of $r$ defines the variation of the population for each individual. If there is one birth and one death for each individual, then $r=0$ . If births outnumber deaths, the population grows.

Definition of carrying capacity in biology

The carrying capacity definition is the maximum size of a population sustainable by a specific environment. When a population reaches the carrying capacity, the net growth rate is $0$ : the number of births equals the number of deaths (and the other factors affecting the number of individuals balance each other).

The population plateaus because the environment can't support more than that number. A temporary increase would necessarily result in a decrease that would bring the number back toward the carrying capacity: we say that the population is controlled by a limiting factor.

What is the limiting factor?

The real world is a world of limitations. Space, food, resources: you name it; they all contribute to keeping the populations down to manageable numbers, and with a reason: the characteristic times of population growth are centuries, if not more, generally outliving the lifespan of a single individual. These extended times allow for careful tailoring of the populations. Only catastrophic events tilt the balance.

🔎 Why do we call the carrying capacity $K$ ? It comes from the German Kapazitätsgrenze, which means "capacity limit".

A combination of the growth rate per individual and the carrying capacity defines the story of a population, from its explosive growth to the eventual plateau and stabilization. What if other factors come and influence the growth of a population? A pandemic, or the discovery of new fertile grounds, are a couple of examples. At that point, both $r$ and $K$ change.

How do I calculate the carrying capacity?

To calculate the carrying capacity, we start from the differential form of the logistic equation.

\frac{\mathrm{d}N}{\mathrm{d}t} = r\times N \times \left(1-\frac{N}{K}\right)

Take the derivative and substitute it with its value at the desired point in the population growth: we can call it $C_p$ . Now we can invert the equation to find the definition of carrying capacity:

K= \frac{N}{1-\frac{C_\mathrm{p}}{r\times N}}

$K$ acts as the attractor of the dynamical system. Every trajectory (the story of a population given a set of initial conditions) converges on the carrying capacity.

Some practical examples of carrying capacity: rabbits and bacteria

Rabbits! Bunnies are the perfect example for studies in population dynamics since they reproduce... like rabbits!

Rabbits were a species unknown in Australia until Thomas Austin introduced a few pairs (12) in 1859 because rabbits reminded him of England. Australia didn't have a natural predator with a specialization in cottontails, which literally recreated the "it's free real estate" meme. Rabbit Inc. was in for serious business, and in six years, the population reached $22$ million individuals.

Believe it or not, we can help you even with the pregnancy of your bunny: visit our rabbit gestation calculator for all your needs while your long-eared pet carries the litter to term. Hopefully, it won't be a million rabbits!

You can pinpoint this tumultuous growth stage in the first part of the population curve: the exponential growth. What happened after?

We know the parameters of this frantic growth:

$r=2.3$ : The next generation had almost two and a half new rabbits for each rabbit. For comparison, the US population had $r=0.4$ in 2020.
$6$ years in, the population was $22,\!000,\!000$ , and the rate of change of the population $C_\mathrm{p}$ was $C_\mathrm{p}=49.12\times10^6$ rabbits per year.

Can we calculate the carrying capacity of Australia for an uncontrolled rabbit population?

\begin{align*} K &= \frac{N}{1-\frac{C_\mathrm{p}}{r\times N}}\\\\ &= \frac{2.2\times10^7}{1-\frac{49.12\times10^6}{2.3\times 2.2\times10^7}}\\\\ &=7.52\times10^8 \end{align*}

The result is in accordance with the outcome of the rabbit baby boom. In 1930, their population reached an estimated $750$ million individuals, a number at which it stopped growing: it touched the carrying capacity.

The story ends in tragedy, though, at least for the rabbits. After this explosive growth, the Australian government decided to introduce a deadly virus for rabbits, myxomatosis. After the infection, in 1950, the population quickly decreased by over $90\%$ . Moral of the story? Don't be like Thomas Austin and keep your country's animals in your country!

Let's take another example. Imagine a bacteria population (the good old E. coli) growing in a welcoming Petri dish. The intrinsic growth rate is $r=2.0$ (perfect mitosis and no deaths). Considering that at the time we are measuring the population, we find that:

The population is $\log{N}=4.75\ \text{CFU/ml}$ ; and
It is growing with a rate of change of $C_\mathrm{p}= 5.05\ \text{CFU/ml}$ per hour.

What's a CFU? CFUs are a widely used unit in laboratories worldwide, the colony-forming unit. It only includes the viable cells, which we consider in a population growth model.

What is the carrying capacity of our Petri dish? Input these values in our calculator (we purposefully left out the measurement units): you will find out that the carrying capacity is $\log{K}=4.75\ \text{CFU/ml}$ . Once our bacteria reach that point, the nutrients and the space in the dish would not allow for growth anymore, but for a certain period of sustained population. Without intervention, a decrease would follow.

If you are interested in the math behind bacterial growth, try our doubling time calculator and our generation time calculator!

Did humanity pass the carrying capacity of Earth?

Science is at the basis of human societies, whether we know it or not. Take, for example, the Haber process, which is crucial to fertilizer production. Its development allowed for the population boom of the 20^th century: to reach one billion, humanity took tens of thousands of years; it took barely more than a century to reach two billion. From 1900 to 2000, however, the population reached six billion, and it is still growing.

The Haber process is often remembered as the most important discovery of the 20^th century. However, shadows cover the ability to turn air into bread: its discoverer also contributed to the development of chemical warfare. Germany's increased agricultural productivity is thought to be a contributing factor to the events of both world wars.

Did humanity reach the Earth's carrying capacity? We don't know. Estimates vary from a mere seven billion (which we passed) to a reasonable 9-10 billion. In any case, there will be a limit to humanity's growth, and it's nearing. Reaching that limit at the speed our species is expanding today would have dramatic consequences, especially dire famines and conflicts (a Malthusian catastrophe or trap: you can read more on this page). We can hope the growth will slow before this, reaching that carrying capacity plateau slowly.

FAQs

What is the carrying capacity in biology?

The carrying capacity is the maximum number of individuals sustainable by a specific environment. This quantity corresponds to a plateau in the population reached after a period of growth or shrinkage. In the logistic model, only a few factors affect the carrying capacity:

The intrinsic growth rate r; and
The rate of change of the population at a given time.

What is the carrying capacity of Earth for a human population?

Between 7 and 11 billion. Scientists don't know the limit to humanity's growth precisely, but they agree that it is close to the current number of individuals hosted on the Planet. If we've already passed Earth's carrying capacity, we will face a phase of rapid shrinking of the population; otherwise, we will meet a plateau (expected for the second half of the century).

How do I calculate the carrying capacity?

To calculate the carrying capacity of a population, we can start from the differential form of the logistic equation:

dN/dt = r × N × (1 − N/K)

where:

r – Intrinsic rate of change;
dN/dt – Change in the number of individuals;
N – Number of individuals; and
K – Carrying capacity.

By defining the rate of change when the population is N as C_p, we can compute the carrying capacity as:

K = N/(1 − (C_p/r × N))

What is the carrying capacity of a population of 100 individuals growing at a rate of 25 individuals per year, and with an intrinsic growth rate r=0.27?

1,350 individuals. To calculate the carrying capacity, first, identify the given data:

r = 0.27;
N = 100; and
C_p = 25.

This combination identifies a particular moment in the growth of a population. The rate of change is rather high, meaning that we are far from the carrying capacity. Let's use the formula to calculate K:

K = N/(1 - (C_p/r × N)) = 100 × 1/(1 − (25/(0.27 × 100)) = 1,350.

What happens if a population passes the carrying capacity?

Since the carrying capacity is a property of the environment and the population together, if the latter passes this critical value, the former will react accordingly. A scenario where a population exceeds the carrying capacity can bring:

Resource scarcity;
More damaging spread of infectious disease;
Degradation of the environment;
Reduced space and territory; and
Unbalance in the population of other species.

If left untouched, nature is usually good at finding a balance and preventing that scenario.

Related calculators

VPD Calculator & Chart (Vapor Pressure Deficit)Sod Calculator Molar Mass Calculator