K-Factor Calculator

This K-factor calculator will assist you in finding the K-factor for sheet metal. Sheet metal is the building block of structures, from forming the body of automobiles to the skin of aircraft wings. The roofs on the house (cf. roofing calculator) or the geyser that supplies water for your warm showers and baths all use sheet metal for the fabrication process. Other applications of sheet metal include piping, medical equipment, machine components, and transformers used in power transmission.

First, the metal is worked into thin sheets for the uses mentioned above and more. It could be any metal as per the demand and loads, but the most commonly manufactured sheets are aluminum, brass, copper, and steel sheets. These sheets undergo different fabrication processes like bending, forming, and punching and are also joined together using welding.

The focus of this article is the K-factor associated with the sheet metal bending process. K-factor deals with the position of the neutral axis, and in this article, you'll learn how to calculate the K-factor.

Before we get into the K-factor, let's look at the bending process for a sheet. You can perform bending using a press brake machine or a bending machine. A press brake consists of a punch and die: the punch presses the sheet down into the die to bend the sheet. The punch and die must be compatible to ensure accuracy and safety.

Let's consider the cross-section of a sheet: the sheet's neutral axis is the line that passes through the points where the stresses and strains are exactly zero. As the punch presses the sheet onto the die, the sheet begins to bend, and the neutral axis shifts.

But why are we concerned about the neutral axis? The neutral axis is the line that divides the cross-section into two regions. The cross-sectional area (see cross-sectional area calculator) above the neutral axis (between the inner surface of bending and the neutral axis) experiences compression stresses. In contrast, the region below the neutral axis (between the outer surface and the neutral axis) undergoes tension. The length of the neutral axis does not change upon bending. Instead, it shifts along the thickness direction of the material.

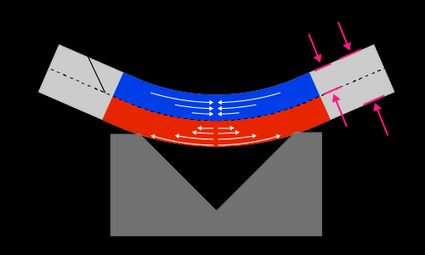
The K-factor is the parameter that tells us about the location of the neutral axis. In other words, the K-factor is the ratio of the location of the neutral axis and the material thickness. Mathematically,

where:

• $K$ is the K-factor;
• $\theta$ is the bend angle;
• $\text{BA}$ is the bend allowance;
• $T$ is the material thickness; and
• $R_i$ is the inner radius.

The neutral axis then lies from the inner surface a distance of the K-factor times the sheet thickness. We denote this distance as $t = K\cdot T$.

Let's calculate the K-factor for a metal sheet having a thickness of $1 \text{ mm}$ and bent to an angle of $90^\circ$. Take the bend allowance as $2.1 \text{ mm}$ and bend radius as $1 \text{ mm}$.

To calculate K-factor:

1. Enter the material thickness, $T = 1 \text{ mm}$.
2. Insert the inner radius, $R_i =1 \text{ mm}$.
3. Fill in the angle of bending, $\theta = 90^\circ$.
4. Punch in the bend allowance, $\text{BA} = 2.1 \text{ mm}$.
5. Using the K-factor calculator:

And so we've found that the neutral axis lies at a distance $0.337$ times the material thickness from the inner surface, i.e. at a distance of