Gambrel Roof Calculator

This gambrel roof calculator is a one-stop tool you can use to find the different measurements and angles of a gambrel roof. You may have your preferred upper and lower roof pitches and want to know the height of your gable. Or you may be visualizing a gambrel roof framing design but don't know where to begin. This tool is for you.

In this gambrel roof calculator, you will learn the following:

• What a gambrel roof is;
• How to calculate gambrel roof angles and dimensions using the two-pitch method;
• What the half-circle method is;
• How to use this gambrel roof calculator; and
• Some frequently asked questions that we will answer for you.

Keep on reading to start learning.

A gambrel roof is a roofing design option in which the roof is divided into an upper and a lower section, where the lower section has a steeper roof pitch than the upper section. We typically see this type of roofing design on barns and houses for its more voluminous attic space than a roof with triangular gables. Below is an example illustration of what a gambrel roof looks like:

Now that we know what a gambrel roof is, let us now discuss how to calculate the gambrel roof angles and the different dimensions of a gambrel roof.

To calculate the different length measurements and angles on a gambrel roof, we first need to label its essential dimensions, as shown in the illustration below:

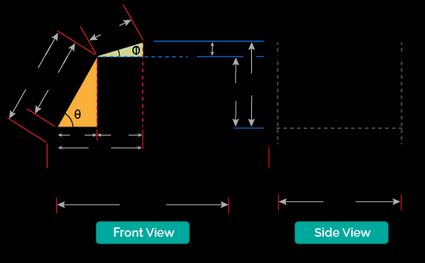
At first glance, we can see that the sum of the upper run length ($x_2$) and lower run length ($x_1$) is equal to half the width of the building ($W$). In equation form, we express that as:

On the other hand, the sum of the upper rise height ($y_2$) and lower rise height ($y_1$) is equal to the total roof rise ($H$), as we can express in this formula:

That means we can easily find one of the runs or rises if we have the other one of them and their sums (half the building width or the total roof rise, respectively).

Consequently, we can also consider the right triangles formed within the gambrel roof, which we highlighted in green for the upper triangle and orange for the lower triangle. Using the basic trigonometric functions, we can find the relationship between the respective run and rise if we know the roof pitch angles of our gambrel roof.

For the upper roof segment, we have these formulas we can use:

where:

• $\phi$ — Upper roof pitch angle (in radians); and
• $R_2$ — Upper rafter length (in the same unit as the run and rise).

For the lower roof segment, we can use the following formulas:

where:

• $\theta$ — Lower roof pitch angle (in radians); and
• $R_1$ — Lower rafter length (in the same unit as the run and rise).

We typically decide on our preferred gambrel roof angles for both the upper and lower roof segments first. Then we decide either how long the upper or lower run length is or how high the upper or lower rise height is. Given those measurements and the relationships we discussed earlier, we can already calculate each and every dimension of our gambrel roof.

Furthermore, we can also calculate the area of the roof to know how much roofing material we'll need for our gambrel roof. For that, we'll need to consider both our roof's gable overhang ($g$) and the eaves overhang ($e$). Here is the formula we need to calculate the upper roof segment area ($A_2$) and the lower roof segment area ($A_1$), respectively:

By multiplying the sum of these areas by $2$, we can find the total roof area ($A_\text{T}$), as shown in this equation:

Lastly, we can also calculate the average volume of our gambrel roof's attic using this equation:

In the half-circle method of designing gambrel roofs, we fit the gambrel roof in a semicircle (or half of a circle), wherein the roof joints touch the semicircle's arc, as shown in the illustration below:

The total roof height is also equal to half the building's width, which is also the radius of the semicircle. Like the two-pitch method, the relationship among the other measurements follows.

By drawing lines from the center of the semicircle's diameter to the joints (the roof's ridge and the gambrels), we can see that we form two isosceles triangles (highlighted in light green and light blue, with peak angles, $\alpha$ and $\beta$, respectively), as shown in the image below:

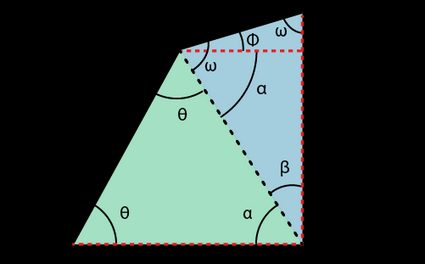
Unnoticeably at first glance, the lower roof pitch is now 45° greater than the upper roof pitch.

We can arrive at that relationship by recalling that the sum of all the interior angles of a triangle is equal to 180°. For the lower triangle, we have the following:

$\alpha + 2\theta = 180^\circ$

where:

• $\theta$ — The lower roof pitch angle and lower isosceles triangle's base angle.

And for the upper triangle, we have this equation:

$\beta + 2\omega = 180^\circ$

where:

• $\omega$ — The upper isosceles triangle's base angle.

Since $\beta = 90^\circ - \alpha$ and $\omega = \alpha + \phi$, we can substitute these equations into the upper triangle's equation to have:

By subtracting this from the equation of the upper triangle's equation, we have the following:

Dividing both sides of the equation by $2$, we now get $\theta - \phi = 45^\circ\\$, giving us the special relationship between the two roof pitches in the half-circle method.

Now that we know the different formulas we used in this tool, let us now discuss how to use this gambrel roof calculator in the next section of this text.

Our gambrel roof calculator features the two methods we can use to calculate the gambrel roof angles and the gambrel roof framing dimensions.

To use the two-pitch method, select the two-pitch calculation method and enter the building length and width, the eaves and gable overhang, and the two pitches of your gambrel roof. After that, you must enter at least one of the following details:

• Upper or lower run length;
• Upper or lower rise height;
• Upper or lower rafter length; or
• Upper or lower roof segment area.

Our tool will automatically calculate the total roof height, the remaining roof details for both the upper and lower roof segments, the total roof area, and the approximate attic volume.

If you only know one roof pitch, follow the same step as above, but you must also enter another value (any other detail listed above or the total roof height).

To use the half-circle method, you must also enter the building length, building width (this will give the total roof height, which is just half the building width), and the eaves and gable overhang.

Finally, enter any of the roof segment details listed below:

• Upper or lower roof segment's roof pitch;
• Upper or lower run length;
• Upper or lower rise height;
• Upper or lower rafter length; or
• Upper roof segment area.

That's it! Now you can find any dimension of almost any gambrel roof design you can imagine.

A gable roof typically has a triangular gable, whereas a gambrel roof has a pentagonal gable for having two-roof pitches. Because of the two-pitch layout of a gambrel roof, the attic volume of gambrel roofs is usually larger than in gable roofs.

The angles of a gambrel roof are the lower roof pitch angle and the upper roof pitch angle. In gambrel roofs, the lower roof pitch has a steeper angle than the lower roof pitch.

To calculate the other gambrel roof pitch for a building with a width of 5 meters and a total roof height of 3 meters, we need to have one of the roof pitches of the gambrel roof. Let's say the lower roof pitch (θ) is 70 degrees and has a run length (x₁) of 1.0 meter.

1. Calculate the lower rise height using the formula:

   y₁ = tan(70°) × 1.0 m = 2.7475 m

2. Obtain the upper rise height, y₂, by subtracting y₁ from the total roof height as follows:

   y₂ = 3.0 m − 2.7475 m = 0.2525 m

3. Determine the upper run length, x₂, by subtracting x₁ from half the building width (5.0 m / 2 = 2.5 m), like this:

   x₂ = 2.5 m − 1.0 m = 1.5 m

4. Finally, calculate the upper roof pitch angle, Φ, using this formula:

   Φ = arctan(0.2525 m / 1.5 m) = 9.556°

The upper roof pitch angle of a gambrel roof with a lower pitch angle of 60 degrees is 15 degrees. Using the half-circle method, we can get that value by subtracting 45° from the lower pitch angle to get 60° - 45°= 15°. Using the two-pitch method, the upper roof pitch can be of any angle less than 60° to have a gambrel roof.