Tree Height Calculator

The tree height calculator is designed to help you where a common measuring stick can not. Of course, you could attempt to take the height measurement of a tree using a ruler; however, that would be troublesome and likely dangerous. That's why we have prepared this risk-free tool that works not only on trees - it can also be used as a building height calculator! What is even better, all you need is your phone. Read on to learn about the science behind measuring the height of a tree using trigonometry!

Trees can be... pretty tall (if you want to discover how they can reach those heights, check out our water potential calculator), and over centuries, people have come up with several ways of telling how tall a tree is. How did our ancestors manage to tell how tall a tree was?

• Thales aptly used the properties of similar isosceles triangles when measuring pyramids. He waited for the shadow of a stick to be the same length as the stick itself, and then he measured the pyramid's shadow, which was also its height. Naturally, this could also be applied to trees.
• Scouts use a similar method, but instead of waiting for the right time of the day, they use a stick that is the same height as the distance from their eyes to their hand. When they are far enough for the rod to "mask" the tree, the straight line's length from the eyes to the base is the estimated tree height.
• Another way is to use the Pythagorean Theorem. However, it is not very practical as it is difficult to tell the distance between the apex and the observer.
• Measuring the height of a tree using trigonometry. This is the method used in our tree height calculator, and although it may sound complicated, don't feel discouraged. In fact, it uses only one function, namely tangent, and the fact that the line at your eye level forms a right-angled triangle with the tree height. The actual formula depends upon the position of the tree.

The measurements required for estimating tree height vary depending on the tree's location relative to you.

• On the same level

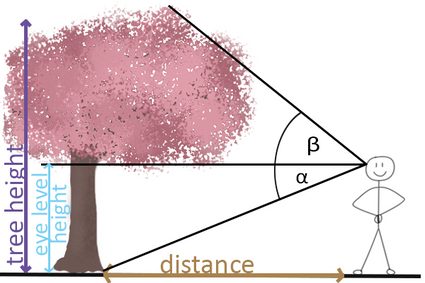
This case is the simplest as we only need to account for the change in height since the viewpoint (e.g., your eyes) is above the ground. The formula is:

tree height = tan(β) * distance from the tree + eye height,

where β is the angle between your eyes and the top of the tree.

Remember that the height of your eyes is not equal to how tall you are. If you do not know this value and can't measure it, you can take α to be the angle between your eyes and the tree's base. Then

eye height = tan(α) * distance from the tree.

• Below the viewpoint

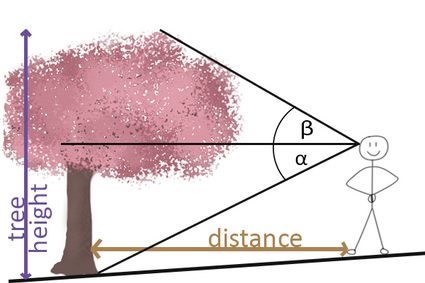
This instance is similar to the previous one, but you cannot use the eye height anymore because we have to also consider the angle of depression. The formula is therefore

tree height = (tan(β) + tan(α)) * distance from the tree.

Most likely, α will be larger than it would have been if the tree had been located on level ground.

• Above the viewpoint

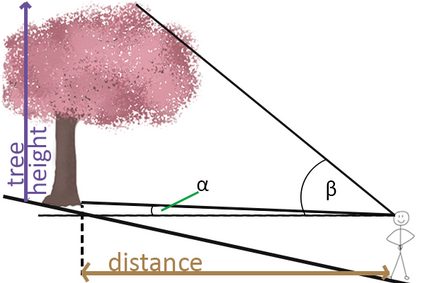
If the tree is on an elevation, the formula changes only slightly and is given by

tree height = (tan(β) - tan(α)) * distance from the tree.

Although the definitions of α and β remain the same, notice that in this case, α is included in β. This is the reason we need to subtract.

Hopefully, you now know how to find the height of an object using trigonometry. Since we already know the size of your tree, there's also a tool to work out its diameter - the tree diameter calculator! 🌳

In case you can't or don't want to trouble yourself with the angle measurement, there is a simpler way - one based on Thales's method of estimating pyramid height. However, it is more universal because you do not have to wait for the proper time of day. In fact, all you need to do is measure the length of your shadow, the tree's shadow, and know how tall you are. Then you can use the following formula:

tree height = (your height * tree's shadow length) / your shadow length.

Bear in mind that this equation tells you only how to calculate the height of a tree if it is on level ground. If the tall object is elevated or located below you, you should opt for the trigonometrical method.

You may think that the trigonometrical method is not very practical. After all, how are you supposed to know the angles? One way could be to use a clinometer, a tool created specifically to determine elevation angle. However, if you do not own one, there is another way. Most of us carry exceptionally versatile devices in our pockets - our smartphones. There are (free!) apps designed specifically to assist you in measuring not only the angles but also the distance. Our calculator also works on mobile browsers so that you can input the results straight away!

As we stated previously, our tree height calculator is multifunctional, and we are about to present an example that is meant to prove it.

Imagine that you want to renovate your garden. After some typical changes, such as seeding fresh grass, you decide to build a treehouse - after all, didn't most of us want to have one at some point in our childhood? To check if you chose a good spot and estimate the amount of materials required, you need to know how tall the tree is. It is located on a small slope upwards, so you move 26 feet away and, using your phone, measure the angle between the base and the top - 54 degrees - and the angle between your eyes and the base - 13 degrees. Inputting this into the tree height calculator gives you the result of 41.79 feet - this tree should be perfect to have a treehouse built on it (assuming it is also robust enough).

However, you are concerned that it could obscure the view from your bedroom. The house is at the same level as you, so you measure the angle between your eyes and the top of the window (treated as β). It is 39 degrees as you stand 20 feet from the building, and since you are 5 feet 6 inches tall, your eye level is approximately at 5 feet 2 inches. Using our tool as a building height calculator, you find out that the window is located at the height of 21.74 feet. Perhaps the treehouse should be moved elsewhere, so as not to block the window.