Elo Calculator

This is an Elo calculator - a fantastic tool that helps you estimate your ♟ chess rating after playing a game, or two, … or even as many as ten. Do you want to know what is the Elo rating system and how it works in practice? Well, here is the right place to begin!

If you're curious, you can find a detailed explanation of the statistical origins of the Elo method and the meaning of Elo rating coefficients in the text below.

The Elo rating system is a method that estimates the relative strength of a player (or team) in a game. In this system, beating a higher-rated opponent gives you more points than beating one with a lower rating. At the same time, your opponent loses as many points as you win.

The name comes from Arpad Elo - the Hungarian-American chess player (and physics professor) who invented it. That's right, Elo is NOT an abbreviation or acronym. It's a surname, exactly the same as in Hooke's and Hubble's law. Funny, huh?

Naturally, the current chess rating system is the best-known Elo ranking (The International Chess Federation, FIDE, provides the official rankings). However, the Elo method (and its variations) is widely used within many other games and sports, e.g., Go, Scrabble, football, and tennis to name a few. Even some online video games base their players' rankings on the Elo algorithm.

Now you should see that the Elo rating system is quite popular. It's high time to look at how to calculate things.

The original idea was to create a system that used a statistical approach. This means that the probability of winning is greater than the probability of losing for a player with a higher ranking. The more significant the difference between opponents, the higher this likelihood is for the higher Elo player.

Having two players, A and B, to find Elo rating change:

1. Take the difference in ratings:

   B - A

2. Divide the difference in ratings by 400:

   (B - A) / 400

3. Find the value of ten to the power of this fraction and add 1:

   10^[(B - A) / 400] + 1

4. The expected score is the multiplicative inverse of the latter:

   expected = 1 / (10^[(B - A) / 400] + 1)

5. Lastly, use the K-factor and the final score (win = 1, draw = 0.5, loss = 0) to get the Elo rating change: Elo change = K × (score - expected).

We can add this result to the previous rating to get the new rating!

K is known as the k-factor, or development coefficient (you can find it in the calculator using the Advanced mode). It usually takes values between 10 and 40, depending on the player's strength (see the dedicated section below for more details).

As you can see, estimating the rating by hand may be painful, so here is our Elo rating calculator that helps you do the math!

Let's take a closer look at the statistical approach that characterizes the Elo system. We assume that every competitor plays at some average level, with some deviations - sometimes they play brilliantly, while sometimes they are below their expectations. In general, we can describe a player's overall performance with a bell curve (or normal distribution) centered at his/her current rating.

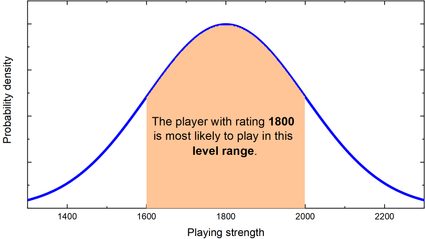
This graph shows that an individual's performance in a game corresponds to a random variable from this distribution. For example, a player with an 1800 rating "plays like a 1500" on a bad day, while on a good day, he can perform as if he was 2200. Usually, he plays around his typical 1800-level.

It is really tricky to estimate an absolute value of performance in practice, but luckily the Elo rating system measures the relative strength between players!

Additionally, a rating of 2000 today may indicate different strength than the same rating one year ago, as such systems experience rating inflations and deflations over time.

Well, knowing that, let's move on to describing the coefficients in the Elo equations.

Let's begin with the mysterious 400 in the Elo rating change formula. The scale is built so that a player with a 400 point advantage over their opponent is ten times more likely to win than to lose. A player with a higher rating of 800 points is 100 times more likely to win, and so on.

The number is arbitrary - if you want a wider range of possible rankings, increase the value, if you want a narrower scale, decrease it.

The k-factor is more intuitive to describe, as it determines how strongly a result affects the rating change. The higher the value, the more drastic the difference is. For example, if the game's score is 1, while the expected score was 0.25, then, for a k-factor equal to 20, the rating will change by 20⋅(1 − 0.25) = 15. If we increase the development coefficient to 40, it doubles the difference to 30 points.

K-factor depends mainly on the strength of players. In chess, it equals 10 for the top players. For children who begin their careers, or players with relatively low rankings, it's set at 40, as young players tend to improve faster over time than the masters.

Feeling confused a little already? What about making some computations to get familiar with the Elo rating system?

Imagine you are playing a rated chess game. Your initial Elo rating is 1750, while your opponent's is 1810. After an exciting battle, you won. What is the change in your Elo rating? At this level of play, we assume that the k-factor is equal to 20. If you want to check or change the development coefficient, go to this calculator's Advanced mode. Let's compute it step by step:

1. Estimate the rating difference, $1810 - 1750 = 60$.

2. Divide it by 400, $^{60}/_{400}$. We can simplify this fraction to $^{3}/_{20}$. We can leave it in this form or convert the fraction to a decimal, which is $0.15$.

3. Raise ten to the power $0.15$ and add one, $1 + 10^{0.15} = 2.413$.

4. Find the expected score by working out the latter's multiplicative inverse, $\text{expected score} = 1 / 2.413 = 0.414.$

5. Evaluate the rating change according to the Elo rating formula, $20\cdot(1 - 0.414) = 11.7$.

6. Finally, add this number to your current rating, $1750 + 11.7 = 1761.7$. Typically, we round Elo ratings to one decimal digit.

Great, you won and gained some points!

Sometimes, it's common to play two games (one as white and one as black) to determine who gets promoted to the next round, especially in knock-out tournaments.

Let's say the second game ended in a peaceful draw. What is the new rating in this case?

• We can repeat the whole procedure, making one change, that the score equals 0.5 instead of 1. Then, sum up both rating updates.

• We can also combine both results into one. The expected outcome will change to $2 \cdot 0.414 = 0.828$, just doubling the number for a single game. In this case, the score equals 1.5. The rest of the computation remains the same.

• The fastest way is to use our Elo calculator! Simply change the option from Single game to Tournament/Multiple games, and type both results.

Whichever option you choose, you should end up with the updated rating equal to $+13.4$. Great job!

Our tool also allows you to choose between a single opponent or multiple ones (like a tournament). We hope that the meaning of the Elo rating system will never trouble you again!

Although the Elo rating system works fine in many fields to estimate players' relative strength, many more methods already do the same. Some are more or less complicated variations of the Elo algorithm, while others take a totally different approach. Here we present a few chess rating systems that are getting more and more popular these days:

1. Glicko rating system - the base of the algorithm is similar to the Elo one. The main difference is that you should always consider two numbers - the rating itself and the Rating Deviation (RD), which imitates standard deviation from statistics. Long story short - the more you play, the lower the RD gets, which means that your ranking represents your real strength with better accuracy. Over time, RD naturally increases when you aren't playing at all.

2. Universal Rating System (URS™) - the one that combines ratings for different time controls into one. There are currently separate FIDE Elo rankings, as they depend on the pace of play (classic, rapid, blitz). Moreover, the more recent a game is, the more it contributes to the overall rating. As a result, your rating may change even if you haven't played a single game for a while.

3. Computer Aggregated Precision Score (CAPS) - this system is quite different from the others. It doesn't consider the games' results but measures the 'greatness' of each individual move and compares them to the best computer moves. It's also a percentage scale - 100% means you are always playings as well as the top chess engine, while 0% indicates that you are always choosing the worst options. It may become helpful as an analyzing tool or even make it possible to compare players from different eras!

Generally speaking, no. A 1000 Elo rating means you are near the middle percentile of all ranked players. The interpretation of this rating varies with each platform too.

There is no clear answer. It is subjective. For example, an Elo rating from 2000 to 2099 at chess.com sits at the 98% percentile, meaning someone with this Elo is better than 98% of players on the platform. However, these players will have a tough time playing against a 2500 Elo player.