Wind Correction Angle Calculator

Welcome to Omni's wind correction angle calculator. This calculator uses vector analysis to determine the correction angle for any wind speed and direction. Using this information, you can compensate for the effect of wind and fly your aircraft along its desired course.

Read on to understand the effect of wind on the aircraft's flight path and how to calculate wind correction angle.

Let us imagine that we want to fly from A to B along the path (desired course) shown in Figure 1, and the wind is blowing across the path from the left. The wind will try to blow us off our desired course. And if we do not compensate for this effect, we will fly along the path shown in yellow (track) and end up at point C.

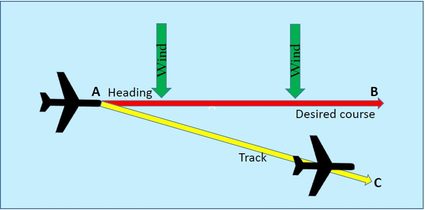
Of course, we don't want to do that unless we are in a movie and are destined to meet someone special (or a horrible end if it's a horror movie) at C! Therefore, a navigator/pilot needs to counteract the effect of wind to maintain the desired course.

The wind correction angle (or WCA) is the correction angle applied to the aircraft's course by pointing its nose towards the wind in such a way that it counteracts the effect of wind. This will ensure that our aircraft follows its desired course.

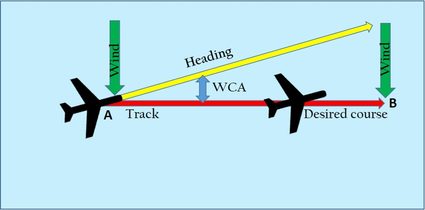
To understand this, let us consider Figure 2. Due to the effect of the wind, the aircraft will tend to drift to the right (as shown in Figure 1). Therefore, we must point the nose of the aircraft to the left to correct this drift. The angle between the heading (i.e., the direction in which the nose of the aircraft points) and the desired course is called wind correction angle.

If you want to learn more about air navigation, you can check the Pilot's Handbook of Aeronautical Knowledge by FAA.

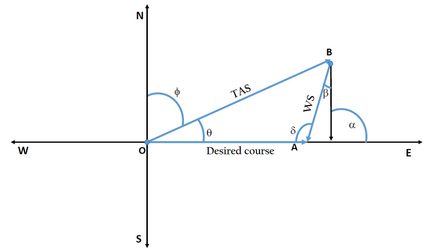
To determine the wind correction angle, let us consider the vector diagram shown in Figure 3, where,

• Vector OA represents the desired course of the aircraft, and $\alpha$ is the azimuth (direction measured in degrees clockwise from the true north) of the desired course.

• Vector BA represents the wind speed ($WS$), and $\beta$ is the wind direction (direction from which the wind is blowing). The azimuth of wind direction is $(180\degree + \beta)$.

• Vector OB represents the true airspeed ($TAS$), and $\phi$ is the azimuth of the heading of the aircraft.

• $\delta$ is the wind angle, i.e., the angle between the wind direction and the desired course:
  $\delta = \alpha - (180\degree + \beta)$.

• $\theta$ is the wind correction angle.

Applying the law of sines formula to the triangle OBA, we get:

The wind correction angle, $\theta$, is calculated by taking the arcsin (inverse sine) of the above function:

The heading of the aircraft, $\phi$, is calculated as: $\phi = \alpha + \theta$

We also recommend checking out our true airspeed calculator and ground speed calculator to learn more about aircraft motion.

Let us see how to calculate the wind correction angle using our calculator. We will consider an example where the flight's intended course is towards the East, and the wind is blowing from the Northeast. Let the true airspeed be 100 knots, and the wind speed is 20 knots:

1. Enter the true airspeed of the aircraft, i.e., 100 knots, in the first row. To choose different units, use the drop-down menu or refer to the knots to mph converter.
2. Enter the azimuth of the desired course of the aircraft, i.e., 90 degrees, in the second-row. Our azimuth calculator can help you calculate the azimuth from latitude and longitude.
3. Enter the speed of the wind, i.e., 20 knots, in the third-row.
4. Enter the wind direction, i.e., 45 degrees, in the fourth row.
5. The calculator will display the calculated wind correction angle, i.e., -8 degrees., in the fifth row.
6. The sixth row will display the heading to be maintained, i.e., 82 degrees.