Last updated: Apr 22, 2024

Wien's Law Calculator

Q: How do I find the temperature using Wien's law?

To find the temperature of any object: Determine the peak wavelength of its emission spectrum. Take the Wien's displacement constant b = 2.8977719 mm·K . Divide this constant by the estimated peak wavelength. That's all! The resulting quotient is the temperature in kelvins. Read more

Q: What does Wien's law reveal about stars in the sky?

Wien's law tells us that there are different star types whose surface temperatures are reflected by their apparent colors . We can deduce that the coldest visible stars are red, while the hottest ones appear blue. Read more

Q: Can you use Wien's law to tell star temperature?

Yes, but it's usually a rough estimate rather than a precise value. That's because Wien's law determines the ideal black body temperature , and not all stars' spectra match this model. There are more accurate techniques to evaluate a star's temperature, e.g., by measuring the total radiated power or checking the color index. Read more

Q: How do I find an A-type star temperature?

Suppose the peak wavelength of the star is λ max = 340 nm : Convert the wavelength to meters: λ max = 3.4×10⁻⁷ m . Divide the Wien's displacement constant by this value: b / λ max = 2.8977719×10⁻³ m·K / 3.4×10⁻⁷ m . The resulting temperature is about 8,523 K . Generally, A-type stars' surface temperature spans 7,400 to 10,000 K. Read more

Table of contents

Wien's displacement law Wien's law formula How to estimate the temperature of the Sun's surface? – example of use FAQs

With this Wien's law calculator, you can easily estimate the temperature of an object, based on the peak wavelength or frequency of its thermal emission spectrum. Read about Wien's displacement law, learn the Wien's law formula, and evaluate the temperature of the Sun's surface, lava, or any hot body by yourself!

🔎 If you want to convert a wavelength to a frequency (or vice versa), try Omni's wavelength calculator!

Wien's displacement law

Wien's displacement law describes one of the relations between the emission spectrum of a black body and its temperature. It states that the higher the temperature, the lower the wavelength λ_max for which the radiation curve reaches its maximum.

The shift to shorter wavelengths corresponds to photons of higher energies. In other words, λ_max (peak wavelength) is inversely proportional to temperature.

The Stefan-Boltzmann law takes into account the total power radiated from a body at any temperature (you can check it in our Stefan-Boltzmann law calculator). Together with Wien's law, they originate from Planck's distribution.

Wien's law formula

The equation describing Wien's law is very simple:

λ_max = b / T,

where:

λ_max – Peak wavelength of light;
T – Absolute temperature of a black body; and
b = 2.8977719 mm·K – Wien's displacement constant.

Although the relation between wavelength and frequency of electromagnetic waves is relatively simple (λ × f = c), we can't work out the peak frequency f_max by this analogy. The reason is that spectral radiance is a sort of energy density function, so its shape and maximum depend on the argument (wavelength or frequency in our case). Knowing that the formula for the peak frequency is:

f_max = k × T,

where k = 5.8789232 × 10¹⁰ Hz/K is a numerical constant.

We can't derive Wien's law formula from classical physics. Numerous observations that confirm this law are among experiments (e.g., photoelectric effect), which contribute to the creation of quantum mechanics.

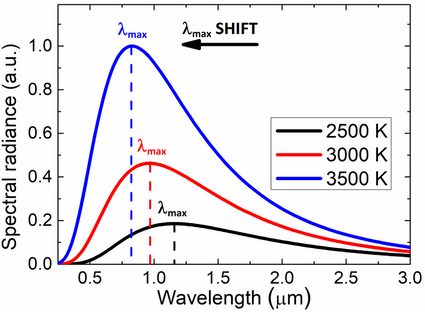
Spectral radiation of a black body as a function of wavelength.

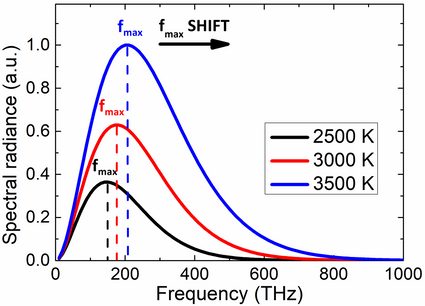
Spectral radiation of a black body as a function of frequency.

How to estimate the temperature of the Sun's surface? – example of use

Do you know how scientists can find the temperature of distant objects? Usually, they perform a spectroscopic observation, fit the Planck function to the measurement, and obtain a parameter that is the temperature.

However, we can also get a nice estimation by applying Wien's displacement law to the results. Let's try to calculate the temperature of the Sun's surface:

Find the peak wavelength of a solar spectrum. It's approximately λ_max = 501.7 nm (or 5.017 × 10⁻⁷ m in the scientific notation).
Transform the Wien's law formula to obtain the temperature: T = b / λ_max = 2.8977719 mm·K / 501.7 nm = 5,776 K.

🔎 If you aren't comfortable with kelvins, feel free to perform the temperature conversion into one of the more standard units. However, remember to always use absolute units during calculations!

Although the black body is just an idealized model, Wien's law is universal and can be a very accurate approximation for real objects. You can also work out the temperature of any body, like hot metal or lava, depending on the color of light it emits – use this Wien's law calculator and find out if the result surprises you or not!

FAQs

How do I find the temperature using Wien's law?

To find the temperature of any object:

Determine the peak wavelength of its emission spectrum.
Take the Wien's displacement constant b = 2.8977719 mm·K.
Divide this constant by the estimated peak wavelength.
That's all! The resulting quotient is the temperature in kelvins.

What does Wien's law reveal about stars in the sky?

Wien's law tells us that there are different star types whose surface temperatures are reflected by their apparent colors. We can deduce that the coldest visible stars are red, while the hottest ones appear blue.

Can you use Wien's law to tell star temperature?

Yes, but it's usually a rough estimate rather than a precise value. That's because Wien's law determines the ideal black body temperature, and not all stars' spectra match this model. There are more accurate techniques to evaluate a star's temperature, e.g., by measuring the total radiated power or checking the color index.

How do I find an A-type star temperature?

Suppose the peak wavelength of the star is λ_max = 340 nm:

Convert the wavelength to meters: λ_max = 3.4×10⁻⁷ m.
Divide the Wien's displacement constant by this value: b / λ_max = 2.8977719×10⁻³ m·K / 3.4×10⁻⁷ m.
The resulting temperature is about 8,523 K.
Generally, A-type stars' surface temperature spans 7,400 to 10,000 K.