Thermal Resistance Calculator

If you're looking for a faster way to find the thermal resistance of a plate, hollow cylinder, or hollow sphere, then our thermal resistance calculator is the right place. Once you select the shape of your object and insert geometric and material properties into our tool, you will end up getting the thermal resistance value. In essence, you can use this tool as a thermal conductivity to thermal resistance calculator for a given shape.

As an extension to thermal resistance calculation, if you are dealing with an object with a hollow geometrical shape, our calculator estimates an extra parameter called the critical radius of insulation, which acts as a limiting outer radius beyond which the object will serve as an insulator.

Now that you know how to use our calculator, would you like to understand the exciting concepts and equations behind it? Please read on to learn more about thermal resistance and the associated thermal resistance formula.

The following points will guide you on how to use our calculator to find the thermal resistance of an object:

1. First, select the shape of your object from the list. Our calculator has three shapes: a plate, a hollow cylinder, and a hollow sphere.

2. After selecting the shape of your object, you can choose an available material from the drop-down menu; it will automatically fill the "Thermal conductivity (k)" field. If you can't find the required material, select "Custom" in the materials list and enter the thermal conductivity value directly into the "Thermal conductivity (k)" field.

3. Based on the selected object's shape, our calculator will show you different geometrical options:

   • A plate
     • First, enter the thickness of your plate.
     • Now, enter the plate's cross-sectional area (A). If you have the explicit values for length and width, you can check the corresponding box to insert them.
   • A hollow cylinder
     • Enter the length of the hollow cylinder, and following that, enter the inner and outer radii.
   • A hollow sphere
     • Enter the inner and outer radii of the hollow sphere.

4. After entering the above values, you will get the thermal resistance of your object.

In addition, if your object is a hollow cylinder or a hollow sphere, the following points will guide you to find the critical radius of insulation:

• Select material or choose "Custom" and insert thermal conductivity value in the "Thermal conductivity (k)" field; and
• Now, insert the convective heat transfer coefficient value of your hollow object in the "Heat transfer coefficient" field to get the critical radius of insulation in the "Critical radius" field.

To understand the importance of thermal resistance, let's tackle a challenge. Let's assume somebody told you to choose the best insulating container out of three containers to preserve the coldness of your cold drink. And imagine that it's a hot day, so you need good insulation to keep the cold drink at a cold temperature. As shown in the figure, you have three containers: glass, wood (oak), and aluminum.

We assume all three containers have the same shape and dimensions and have the following thermal conductivity values:

• $\text{Glass = 0.78 W/(m}\cdot\text K)$;
• $\text{Wood (oak) = 0.17 W/(m}\cdot\text K)$; and
• $\text{Aluminum = 237 W/(m}\cdot\text K)$.

At the end of this article, we will find the answer by using our thermal resistance calculator. Firstly, let's try to understand what thermal resistance is.

Formally, thermal resistance $R$ is defined as the ratio of the temperature difference $T_2-T_1$ and the heat flow $Q_{1-2}$ between two points $1$ and $2$:

The SI unit for thermal resistance is K/W.

Informally, we define thermal resistance as the ability of the object of specific geometry and material to resist the flow of heat. Thermal is derived from the Greek word therme, which means heat. Combined with resistance becomes thermal resistance, which means heat obstruction.

Unlike thermal conductivity, which depends only on the object's material, thermal resistance depends both on the material and shape of the object. Good insulators are objects which have a higher thermal resistance. The following section will look at various shapes and corresponding thermal resistance formulas.

Common shapes are the geometry of the objects present all around us. This article focuses on three common shapes: a plate, a hollow cylinder, and a hollow sphere. You can find each object's geometry and corresponding thermal resistance formula below:

A plate

A plate is a thin rectangular block whose thickness ($t$) is lesser than its length ($l$) and width ($w$), i.e., $l>>t$ and $w>>t$ as shown in the figure below. The figure shows a plate with a thickness ($t$), length ($l$), and width ($w$), with temperatures $T_1$ and $T_2$ across the thickness ($t$).

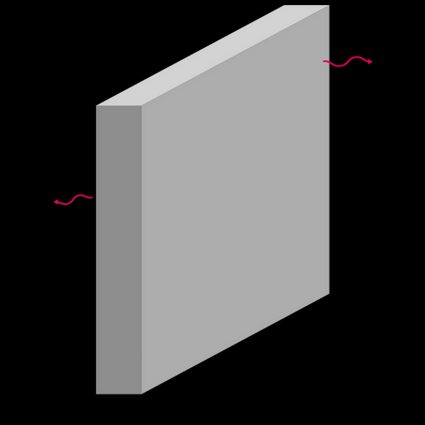
Some examples of a plate are a windowpane and a wall. Below is the thermal resistance formula:

where:

• $R_{\text{plate}}$ — Thermal resistance in $\text{K/W}$;
• $k$ — Thermal conductivity of the material $\text{W/m}\cdot\text K$;
• $t$ — Length of the plate in$m$; and
• $A$ — Cross-sectional area, i.e., $A=l \times w$ in $\text m^2$.

A hollow cylinder and hollow sphere

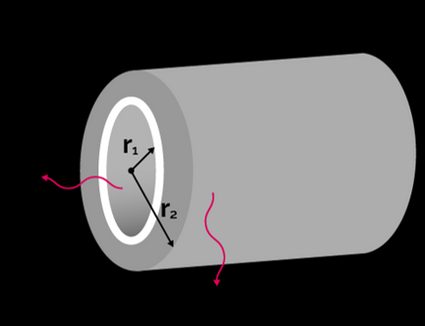
A hollow cylinder is a tubular structure of finite length $L$ with $r_1$ and $r_2$ as its internal and outer radii. When you cut out a sphere of radius $r_1$ from the sphere of radius $r_2$, the obtained spherical geometry is called a hollow sphere.

In the below figure, we can see a hollow cylinder of length $L$ with inner radius $r_1$ and outer radius $r_2$; with temperature $T_1$ and $T_2$ at $r_1$ and $r_2$, respectively.

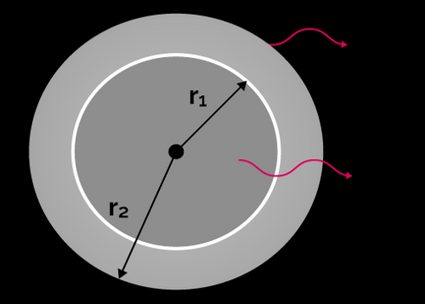
In the next figure, we have a hollow sphere with inner radius $r_1$ and outer radius $r_2$; with temperature $T_1$ and $T_2$ at $r_1$ and $r_2$, respectively.

The thermal resistance equation for both geometries is given by:

where:

• $R_{\text{cylinder}}$ and $R_{\text{sphere}}$ — Thermal resistances for hollow cylinder and hollow sphere respectively in $\text{K/W}$;
• $r_1$ and $r_2$ — Internal and outer radius, respectively, of both the geometries in $\text m$ (refer to the figure);
• $L$ — Length of the hollow cylinder in $m$; and
• $k$ — Thermal conductivity of the material $\text{W/(m}\cdot\text K)$.

Many domains in science provide us with surprisingly similar equations. For example, in the Coulomb's law calculator in electromagnetism and the gravitational force calculator in Newtonian mechanics, you'll find similar governing equations. In the same line, we can analyze the thermal resistance equation in heat transfer by drawing an analogy with the electric current flow equation. This section will briefly look at how we can achieve that.

In the 17th century, a French mathematician called Jean-Baptiste Joseph Fourier developed an empirical relation for conduction heat transfer, known as Fourier's law of heat conduction. A simple form (the one-dimensional case) of Fourier's law is the equation (5), which describes the heat flow across a medium with temperature difference:

where:

• $Q$ — Rate of heat flow given in $\text W$ across the temperature difference $\Delta T$ given in $\text K$;
• $A$ — Cross-section area perpendicular to the direction of heat flow in $\text m^2$; and
• $\Delta x$ — Distance over which the heat flows.

If our object is a plate, then in the above equation, we replace $\Delta x$ by thickness $L$. With some rearrangement of terms, the equation becomes:

Now, let us look at Ohm's law, which describes the current flow across a voltage difference:

where:

• $\Delta U$ — Electric potential difference between two terminals in $\text V$ (volts);
• $I$ — Current flow across the terminal in $\text A$ (amperes); and
• $R$ — Resistance offered by the object against the current flow given in $\Omega$ (ohms).

(Learn more about it in the Ohm's law calculator.)

Rearranging the above equation:

By comparing equation (6) and equation (8), we can notice the following analogies:

• The voltage difference across the terminal is similar to the temperature difference across the medium (or the object);
• Current is similar to heat flow; and
• Thus, the term $L/(kA)$ is equivalent to having a thermal resistance for Fourier's law similar to electrical resistance for Ohm's law.

For the plate case, if we increase the thickness $L$, the cross-section area $A$ remains the same. As a result, it continually reduces heat flow across the plate. Whereas for hollow geometries such as a hollow sphere or a hollow cylinder, as the thickness (or outer radius) increases, the convective heat transfer becomes dominant, increasing heat flow. Thus, a quantity called critical radius is defined to establish a condition on the outer radius.

The critical radius of insulation is a threshold parameter that determines the limit on the outer radius of a hollow cylinder or sphere to reduce the heat transfer.

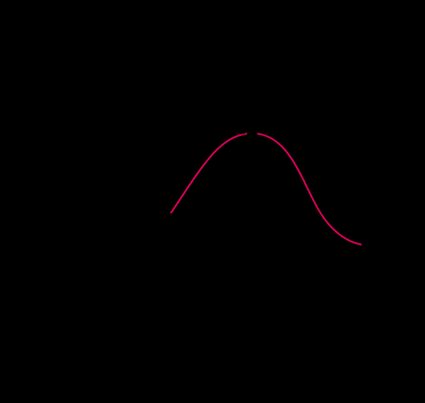
The figure shows the variation of heat flux from the hollow object vs. radius. $r_1$ indicates the internal radius. As we increase the thickness, the outer radius will increase. This increase in radius, in turn, increases the heat flux; this occurs because the area available for convective heat transfer has increased. At a certain outer radius value called critical radius $r_{\text{cr}}$, we notice a maximum heat flux. After $r_{\text{cr}}$, heat flow is smaller. Thus, to reduce the heat flow, we need to satisfy the $r_2>r_{\text{cr}}$ condition.

The following are the critical radius of insulation equations for a hollow cylinder and a hollow sphere:

where:

• $h$ — Heat transfer coefficient between the hollow structure and the medium surrounding it in $\text{W/(m}^2 \text K)$.

Let us go back to our thermal resistance challenge, which asked you to choose the best container to preserve the coldness of our cold drink. Now that you have learned what thermal resistance is and how to calculate it for different shapes, it shouldn't be a problem for you! The following steps summarize the solutions to the challenge:

1. Firstly, you can approximate the container shape as a hollow cylinder (no way as a plate!).

2. After that, choose the selected shape and insert the geometric property of the container.

   In our challenge, let's assume the following geometric properties of the container: length $L=0.5\ \text m$, inner radius $r_1=0.1\ \text m$, and outer radius $r_2=0.2\ \text m$.

3. Finally, insert the thermal conductivity of the material. In the following table, you will see the material property and corresponding thermal resistance value of each container. You obtained these values by using the thermal resistance formula embedded inside our thermal conductivity to the thermal resistance calculator.

The table shows that a wood container has a higher thermal resistance than the other two. As a result, the wood container is the best insulation container that can preserve the coldness of the cold drink.

Hurray! We hope you have learned a lot about thermal resistance. If you want to extend the knowledge gained from this article, please check out our heat transfer coefficient calculator, which provides an opportunity to apply the knowledge that you gained here to multilayer plates!