Thermal Equilibrium Calculator
The thermal equilibrium calculator helps you determine the final temperature between two elements or systems that are transferring heat between them. In this article, we will start explaining the thermal equilibrium definition, the thermal equilibrium equation, and how to calculate it.
What is thermal equilibrium?
First, let's explore why heat transfer occurs: Heat flows from a high-temperature area to a low-temperature area. As long as there is a temperature difference, there will be heat transfer. The heat flow rate is determined by several factors, but one of the most important ones is heat capacity, as we explain it in the specific heat calculator. We can see its use in the next formula:
where:
- — Supplied or subtracted heat (in joules);
- — Mass of the object, in kilograms;
- — Heat capacity, in J/(kg·K); and
- — Difference between the initial and final temperatures in kelvin.
Notice that by modifying an object's mass, heat capacity, or temperature difference, you can increase or decrease heat transfer. Also, take a look at the fact that when two objects have the same temperature, no heat transfer occurs. This state, called thermal equilibrium, occurs when the objects have reached a common temperature and can no longer exchange heat.
In the following graphic, we can see how temperature changes through time and reaches equilibrium between two objects:
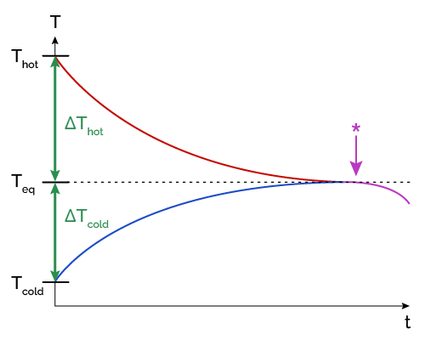
How to calculate thermal equilibrium
Now that we have understood what thermal equilibrium is, let's apply the heat transfer equation to a situation where two objects or systems are exchanging heat.
If both objects are in contact for a sufficient amount of time, they will eventually reach thermal equilibrium. This is because the temperature difference between the objects becomes zero, and there is no longer any heat exchange, as explained in the picture above.
Assuming no heat loss, we can say that the heat supplied by one object is the same as the heat absorbed by the second one. Consequently, in terms of the thermal equilibrium equation, we have:
where:
- and — Represents the heat transferred between object 1 and object 2.
Now, if we re-arrange the equation above, and we only consider specific heat (object-only experiments temperature variation, no state phase change), we have:
where subscripts and refers to objects one and two, and & refers to final temperature and initial temperature, respectively.
Finally, because of the thermal equilibrium definition, we are going to reach the same final temperature, meaning there will only be one temperature. Therefore:
How to calculate thermal equilibrium including latent heat
So far, we have discussed how to calculate thermal equilibrium in situations where there is no phase change. However, as we detail in the latent heat calculator, the process of changing phase from one state to another can require a significant amount of heat transfer. Thus, the thermal equilibrium equation has to account for it:
where:
- — Specific latent heat, expressed in J/(kg);
- — Heat absorbed or released depending on the direction of the phase transition;
- — Specific heat: Heat absorbed or released during temperature change (no phase change is involved); and
- — Represents the total heat exchanged with the other object until equilibrium
The specific latent heat is different for solid-to-liquid transition and liquid-to-gas transition. To convert 20 grams of ice into water, you need to provide an amount of energy equal to 6680 J, which is the specific latent heat of the solid-to-liquid transition. To turn the same amount of water into vapor, you need to provide an amount of energy equal to 45,294 J, which is the specific latent heat of the liquid-to-gas transition.
With the last equation, we could determine the equilibrium temperature if the object is in contact with another object, as we will see in the following example.
How do you calculate thermal equilibrium temperature? – Real life example
Similarly to what is covered in the chilled drink calculator, there are many strategies for cooling a beverage, not only adding ice to it. Other methods might involve bottles covered with napkins for increasing conductivity, as explained in the thermal conductivity calculator; others would look for increasing the as explained above. In any case, what such strategies are doing is modifying the parameters involved in the thermal equilibrium equation.
In this example, we will assume we are adding 100 grams of ice at 0 °C to 0.5 liters of water at 20 °C and that we want to know the final temperature (thermal equilibrium temperature). Also, you can verify the results in the handy thermal equilibrium calculator. You will need to include the latent heat option.
-
Find out the specific heat coefficient for liquid water and the latent heat coefficient for water fusion . Also, obtain the water-specific heat coefficient (20°C):
-
; and
-
.
Notice the suffix "p". It refers to the fact that we are going to cover a thermal process at constant pressure.
-
-
Define your first equation: Heat transfer by the ice. We will assume it fully melts and increases its temperature from 0 °C to a certain thermal equilibrium temperature: .
We are adding the subscript to indicate it refers to the first object: the ice. Consequently, the subscript will refer to the 20 °C water.
- Build your second equation: Heat transfer by the water:
- Use the thermal equilibrium equation: , we obtain .
Beware, we assumed the ice would fully melt and reach an intermediate temperature between ice temperature and 20 °C water. However, if there had been enough ice at a lower temperature, the 20 °C water would have been frozen. That is why you have to be sure of what kind of result is logical for the situation.
If the equation provides a temperature higher than the original hot object or lower than the cold object, then you know you made wrong assumptions and have to start over again.
FAQs
What is the zeroth law of thermodynamics?
The zeroth law of thermodynamics establishes a reference temperature for the measurement of temperature. It defines that if two objects or systems are each in thermal equilibrium with a third system, then the first two objects are in thermal equilibrium with each other.
Imagine first calibrating a thermometer with a calibration pattern. Then, because you have the thermometer scale based on the pattern, you can use it as a reference for measuring a third object, fulfilling the zeroth law statement.
How can thermal equilibrium be achieved?
Objects or systems achieve thermal equilibrium when both have the same temperature. At that moment, there is no more heat transfer. Thermal equilibrium can be achieved through any of the heat transfer mechanisms, such as convection, conduction, and radiation.
How can thermal equilibrium be measured?
Here is a list of steps for measuring thermal equilibrium:
-
Define the number of objects that are interacting. Let's say: 2.
-
Obtain two thermometers. Record the initial temperature of each object.
-
Put the objects in contact and wait until both thermometers have reached the same temperature value.
Congratulations! The objects have achieved thermal equilibrium.
Will 1 kg of ice freeze 1 kg of water?
Assuming the ice temperature is 0 °C and the water temperature 20 °C, the latter will freeze. Use the thermal equilibrium calculator or:
-
Remember, if the ice melts fully, that will require a latent heat of 334 kJ.
-
Calculate the heat released for a 20 °C change (1 kg of water, 20 °C to 0 °C): 83,620 J.
-
Notice that the heat released by water from 20 °C to 0 °C is less than the required latent heat: 83,620 J < 334 kJ, meaning that the liquid water will not be able to melt the ice but instead will freeze.