Skin Depth Calculator

Use the skin depth calculator to determine the skin depth in conductors at any signal frequency.

Have you ever wondered why RF antennas are made from hollow tubes, not solid rods? If you have, then our article on the skin depth effect may help you in satisfying your curiosity.

Continue reading to know what skin effect is and the formula for skin depth calculation. You will also find an example of how to calculate skin depth in a conductor.

When a DC signal flows through a conductor, the current is distributed uniformly throughout the cross-section of the conductor (see Figure 1 (a)).

On the other hand, when an AC signal flows through a conductor, the distribution of current is not uniform over the entire cross-section. The current density is higher at the surface of the conductor and decreases exponentially as we move towards its center (see Figure 1 (b)).

We call this phenomenon of non-uniform distribution of an alternating current in a conductor the skin effect.

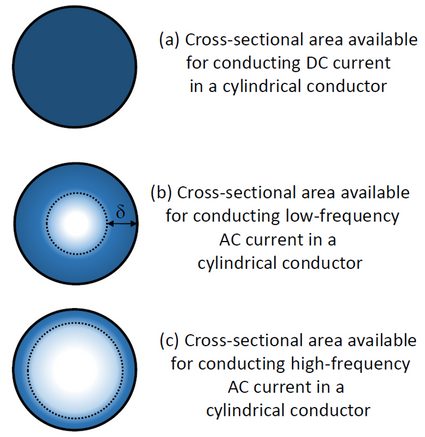
Skin effect depends on the frequency of the AC signal; the higher the frequency, the more pronounced the effect. At high frequencies, the conducting area is restricted to a very thin skin on its surface (see Figure 1 (c)).

When an alternating current flows through a conductor, the magnetic flux linked with the conductor changes with the change in the magnitude and direction of the current.

According to Faraday's law of electromagnetic induction, the changing magnetic flux induces a current in the conductor. This induced current is called eddy current, and it creates an electric field that opposes any change in the alternating current flowing through the conductor. This effect is strongest at the center, and hence, the current is forced to flow closer to the surface.

Skin effect increases the effective resistance of a conductor by reducing the cross-sectional area available for conducting current. In fact, the effective resistance offered by the conductor is greater for AC than for DC. This results in a larger power loss for a given average value of alternating current as compared to the power dissipated for the same value of direct current.

The region between the outer surface and the point where the current density drops to about 1/e or 37% of its value at the surface is called the skin depth (see figure 1 (b)).

Skin depth depends on the properties of the conductor, i.e., its size, resistivity, magnetic permeability as well as the frequency of the signal. To calculate skin depth, we will use the formula:

where:

• $\delta$ — Skin depth;

• $\rho$ — Resistivity of the conductor;

• $f$ — Frequency of the AC signal;

• $\mu_0 = 4\pi \times 10^{-7}\ \rm H/m$ — The permeability of free space; and

• $\mu_r$ — Relative magnetic permeability of the conductor. Check out the magnetic permeability calculator to learn more about permeability.

To further understand the concept of skin depth, let us study the effect of frequency on current density distribution in copper wire.

1. The resistivity of copper at room temperature is:

   $\rho= 1.678\ \rm \mu\Omega\cdot cm$,
   $\rho = 1.678 \times 10^{-8}\ \Omega\cdot \rm m$

   and the relative permeability is:

   $\mu_r = 0.999$.

2. We will first consider a copper conductor carrying an AC signal at a frequency of 50 Hz (typical frequency of AC signals used in homes). We can calculate the skin depth at this frequency as:

   $\delta = \sqrt{\frac{1.678 \times 10^{-8}\ \Omega\cdot {\rm m}}{3.14 \times 50\ \text{Hz} \times 1.257 \times 10^{-6}\ \rm H/m \times 0.999}}$

   $\delta = 9.22\ \rm mm$

   So, if we use a wire of diameter less than 1 cm, the skin effect is negligible for AC signals at typical frequencies used in the home.

3. Now will consider the same conductor carrying an AC signal at a frequency of 2.4 GHz (in radio frequency range). We can calculate the skin depth at this frequency by using the given values in skin depth equation:

   $\delta = \sqrt{\frac{1.678 \times 10^{-8}\ \Omega\cdot {\rm m}}{3.14 \times 2.4 \times 10^9\ \text{Hz} \times 1.257 \times 10^{-6}\ \rm H/m \times 0.999}}$

   $\delta = 1.3308\ \text{μm}$

   Here, we note that at radio frequencies, the current flows only through an extremely thin region (within a few μm) near the surface. That is why we use hollow metal tubes in antennas and RF conductors to save both cost and effort in managing heavy solid metal rods.

Now, let us see how we can calculate the skin depth in copper using our skin depth calculator.

1. Using the drop-down menu, select the material, copper.

2. The resistivity and relative permeability fields will auto-populate. You can also enter these values if you know them for another material by selecting the custom option at the bottom of the list. Our conductivity to resistivity calculator can come in handy if you know the conductivity and want to determine the resistivity.

3. Enter the frequency of the AC signal, e.g., 2.4 GHz.

4. The skin effect calculator will display the skin depth in copper at 2.4 GHz, i.e., 1.3308 μm.