Root Mean Square Speed Calculator for Ideal Gas

Our root mean square speed calculator gives you an effortless way to calculate the RMS speed for an ideal and mostly monoatomic gases. To calculate, we need to:

1. Choose the gas from the presets – or alternatively, choose the "custom" option and enter the molar mass of the gas,
2. Input the temperature of the gas,
3. Woosh, your result is instantly computed!

A good thing to remember is that RMS is not the median or average speed (as simple average speed would be equal to zero, as particles are moving in every direction), but it provides a good approximation of particles' movement.

An ideal gas, as defined in the kinetic theory of gases, is a model for simple gas behavior. When using ideal gases, we have to make a few assumptions:

• Container is non-movable. It always stays in one place.

• Particles of the ideal gas are so small that their volumes become negligible.

• Particles constantly collide with themselves and the walls of the container. Collisions are fully elastic, meaning that kinetic energies are conserved.

• Any interactions between particles except for collisions can be neglected. We do not need to worry about gravity or electromagnetism.

• Particles are in constant and random motion. They keep bouncing off each other in a pretty much random fashion.

Those assumptions allow our root mean square speed calculator to calculate things correctly.

The formula below is used for calculating the RMS speed in our calculator:

where:

• $v_{rms}$ – Root mean square speed;
• $R$ – Gas constant;
• $T$ – Temperature of the gas in kelvin – you can easily convert from Celsius using the celsius converter; and
• $M$ – Molar mass of the gas. Some molar masses are already given in our calculator as presets.

However, the other formula based on Boltzmann's constant exists:

where:

• $k$ is Boltzmann's constant. Roughly equal to $\small 1.380649\! \times\! 10^{-23}\ \rm m^2\ kg\ s^{-2}\ K^{-1}$;
• $T$ is the temperature of the gas in kelvin; and
• $m$ is the mass of a single particle.

Our calculator has the former equation implemented, as it's the one used more often.

We've implemented seven gases in our calculator – please note that some of them can be approximated as ideal gases within reasonable tolerances around standard pressure and temperature (air, carbon dioxide, water vapor).

To input other gas than the preset options, choose "Custom" and enter the molar mass of your ideal gas. You can use the table below to find the molar masses for other gases.

The root mean square speed formula used in our calculator may be derived from the ideal gas law formula (see the ideal gas law calculator for more):

where:

• $P$ – Pressure of the gas;
• $V$ – Volume of the gas;
• $n$ – Number of particles of the gas;
• $R$ – Gas constant; and
• $T$ – Temperature of the gas.

We need to employ the kinetic energy formula, but we have to alter it to match our assumptions about gases.

We have to calculate each particle's kinetic energy; therefore, we change the mass of the entire gas ($m$) to one based on the molar mass ($M$) and the amount of particle ($n$):

and by knowing that $\frac{3}{2} PV$ (only in monoatomic gas) is equal to $E_k$, we can arrange an equation:

So, we can now square root both sides and get the root mean square speed formula:

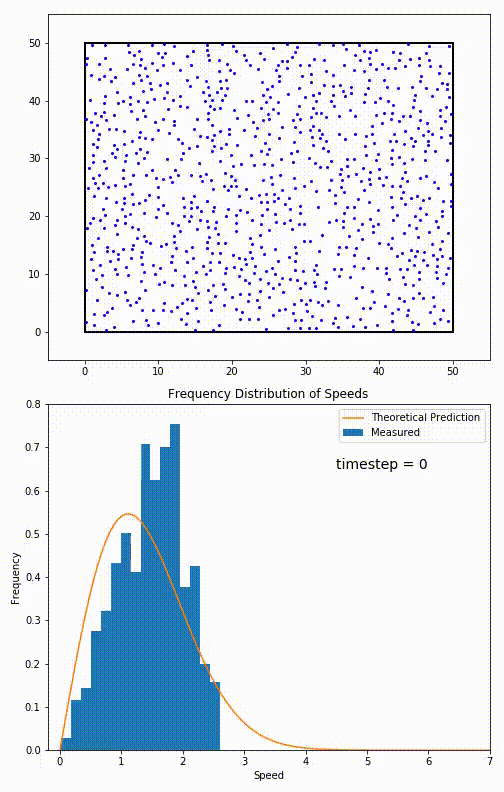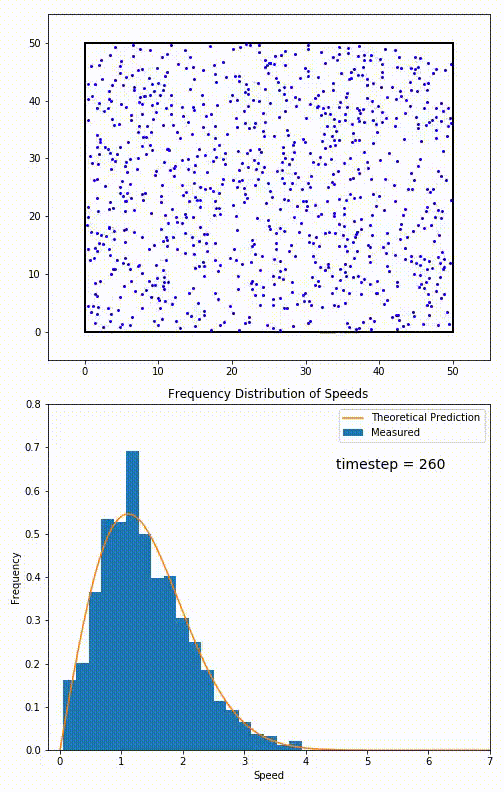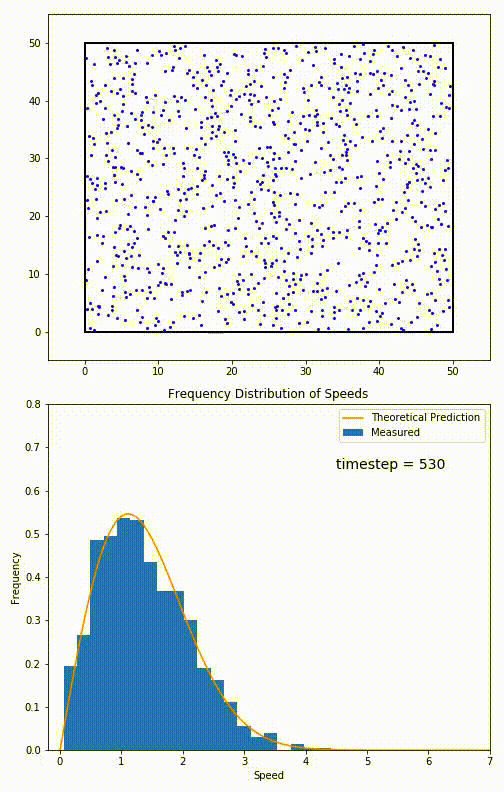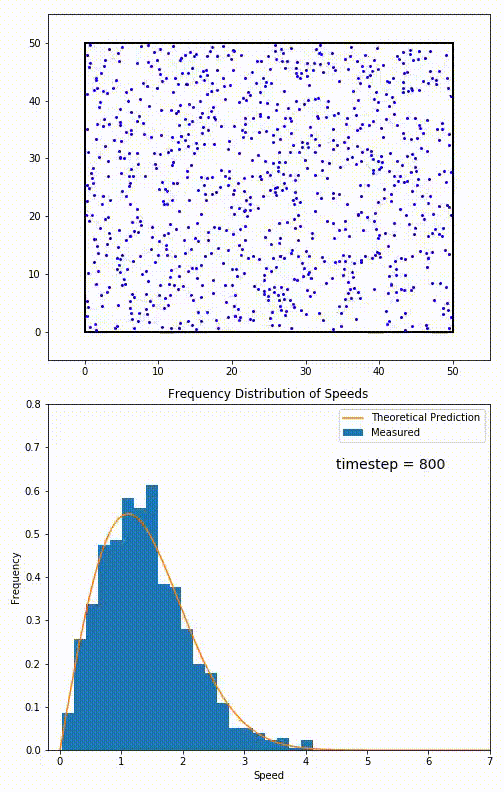
The root mean speed of gas corresponds to the speed of particles having the median kinetic energy. Particles have their expected speed, but they can have different velocities because of the collisions at each timestep.

The distribution of speeds mathematically can be assigned to an astoundingly expressive function:

where:

• $m$ – Single-particle mass;
• $k$ – Boltzmann's constant; and
• $T$ – Temperature in kelvin.

Below you can see the probability density function that arises from experimental data:

502.4 m/s. Here is how to calculate this result:

1. Convert 20 °C to kelvin by adding 273 to get the result 293.
2. Multiply by 3 times the gas constant, which is 8.314 J/(K·mol).
3. Divide by the molar mass of air, which is 0.028965 kg/mol.
4. Take the square root to get the answer of 502.4 m/s

The root mean square (RMS) speed of a gas is directly proportional to the square root of the absolute temperature (measured in kelvins). Temperature is a measure of the average kinetic energy of the particles that make up a gas, and the RMS speed is a measure of kinetic energy. Therefore the higher the temperature, the higher the RMS speed.