Pump Horsepower Calculator

The pump horsepower calculator is used to estimate the pump power, i.e., the power transmitted to the shaft. A pump is one of the most common hydraulic machinery and is used to move fluid by the means of mechanical action by its impeller. Some of its application includes maintaining water supply across the city, heating, ventilation, and cooling systems (HVAC), hydraulics and pneumatics, and electricity generation (see hydroelectric power calculator)

The pump power is a function of hydraulic power and efficiency. Given the importance of this component, it is imperative to understand the basic characteristics of a pump to ensure greater efficiency of the larger processes. You can find more information about pump efficiency and pump power calculations in subsequent paragraphs.

If you are interested in engine horsepower, visit our horsepower calculator.

A pump is a device used to move fluid using mechanical actions. The most common components of a pump are the impeller, casing, suction pipe, and delivery pipe. Pumping action involves drawing of fluid via the suction end of the pipe and moved across the body of the pump over to the delivery end of the pipe. To do so, the impeller, which is housed inside the casing, moves either by rotating or reciprocating motion, depending on the type of pump. The impeller is connected to the shaft, which is run by an electric motor.

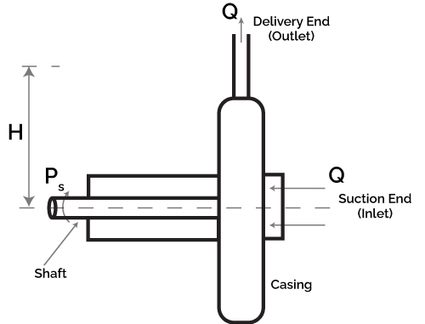
The pump shaft power is defined as the power applied to achieve the head and the volumetric flow rate. It is a function of volumetric flow rate Q, differential head H, the density of fluid ρ, efficiency η, and the gravitational constant g. Mathematically, that's:

Similarly, the hydraulic power can be estimated as:

The efficiency, therefore, can be rewritten as the ratio of hydraulic power to shaft power:

The above equations are valid given the parameters have the following units.

• Volumetric flow rate Q is in $\mathrm{m^3/s}$.
• Head H is in metres.
• Efficiency η is on a scale of 0 to 1.

We know that the pumps in most cases do not operate at an efficiency of 100%. Actually, cavitation drastically reduces it. The parameter of specific speed is used to compare the performance of the pump to the ideal case, i.e., a geometrically similar pump delivering 1 cubic meter of fluid per second against 1 m head. The specific speed $N_\mathrm{s}$ is a dimensionless quantity that is given by the equation:

where the speed of pump N is in radians per second.

Note that, while $N_\mathrm{s}$ is dimensionless, its value changes depending on the units system used for its inputs. The above version of the equation is used in the calculator that gives dimensionless output for specific speed. However, a simpler version of the equation was introduced without the acceleration due to gravity g to use with English units. Mathematically,

The user has to make sure the units used are consistent for the above equation. Such that:

• Discharge Q is in gallons per minute;
• Head H is in feet; and
• Speed N is in rotations per minute.

To calculate the shaft power of a pump:

1. Enter the discharge or fluid flow rate, Q.
2. Insert the differential head, H.
3. Fill in the density of the fluid, ρ.
4. Enter the efficiency of the pump, η.
5. The pump horsepower calculator then returns the value of shaft power and hydraulic power.

Further, to estimate the specific speed of the pump:

6. Enter the pump speed or revolutions, N.
7. The specific speed of the pump is returned by the hydraulic horsepower calculator.

Let's take a look at a pump shaft power calculation:
Determine the pump power supplying water at 10 cubic meters per hour with the differential head of 3 m. Take the efficiency of the pump as 79%.

To calculate the shaft power of a pump:

1. Enter the discharge or fluid flow rate, $Q = 10~\mathrm{m^3/h}$.
2. Insert the differential head, H = 3 m.
3. Fill in the density of the fluid, $\rho = 1000~\mathrm{kg/m^3}$.
4. Enter the efficiency of the pump, η = 0.79.
5. The shaft power equals to:

6. The hydraulic pump power calculation can be performed as: