Prandtl Meyer Expansion Calculator

If you are thinking of finding the supersonic flow Mach number after an expansion wave, this Prandtl Meyer expansion calculator is the perfect match for you. Our calculator will help you find the Mach number along with downstream flow properties.

Please read the following article to learn about:

• What is an expansion wave, and how are they generated?
• What is the Prandtl Meyer theory, and how to evaluate Prandtl Meyer function?
• How to use the Prandtl Meyer expansion calculator?

When a supersonic flow encounters a surface that folds outward, the flow will have more space to move, leading to an expansion of the flow. This expansion is assisted by a fan of waves called an expansion wave, which acts as a continuous boundary where the expansion happens.

In 1907, German fluid dynamicist Ludwig Prandtl studied the expansion waves, followed by his student Theodor Meyer in 1908. They developed a theory called Prandtl Meyer expansion to explain the behavior of expansion waves. We will briefly look at the theory and the equations behind our Prandtl Meyer expansion calculator in the following paragraphs.

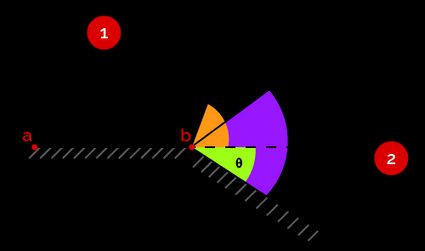
Below, in the figure, you can observe a surface folding in the outward direction. A flow with Mach number $M_1 ( M_1>1)$flows along the parallel surface (a-b). Because of the outward folded surface (after surface a-b), we notice the generation of an expansion wave. This expansion wave lends itself as a fan of waves. The flow passing through this fan of waves changes the direction of the flow. After the expansion wave (region 2), the flow will have a Mach number $M_2$ with its direction changed by an angle $\mu-\theta$. The properties in the region after the expansion wave are denoted by $T_2$, $P_2$, and $\rho_2$.

According to Prandtl Meyer theory, you can find the downstream flow properties by using the following steps:

1. Find the Prandtl Meyer function $\nu(M1)$ for the upstream Mach number $M_1$ with known specific heat ratio $\gamma$ of the fluid medium. We can use the following equation to do that:

2. Now use the deflection of the surface $\theta$ and find the $\nu(M2)$ using the following equation:

3. Use the $\nu(M2)$ to find the Mach number in the downstream region with known $\gamma$ of the fluid medium. You can again make use of the Prandtl Meyer function:

4. The above equation is transcendental, and you can solve for $M_2$ either by iterative method or by using the Prandtl Meyer function – Mach number tables.

5. As the expansion wave is isentropic, we can use the equations of our isentropic flow calculator to find the flow properties. Once you know the upstream properties, you can use the following equations to find pressure, temperature, and density, respectively:

Good job! You have successfully understood how to find the downstream properties of an expansion wave. Use our calculator to avoid all these tricky calculation steps and get answers at supersonic speed ;).

To use our Prandtl Meyer expansion calculator, use the following instructions:

1. First, based on your requirement, you can choose YES/NO for the "Do you want flow properties ?" option. If you want only the Mach number and Mach angles, you can set it to "NO": you need only the upstream Mach number $M_1$ and deflection angle $\theta$. If you want downstream properties: pressure, temperature, and density, you should choose "YES": along with upstream Mach number $M_1$ and deflection angle $\theta$, you must provide the upstream temperature, pressure, and density.
2. Let us assume that we choose YES for the "Do you want flow properties ?" option, as this is more general.
3. Now, you can insert upstream Mach number, deflection angle, and upstream flow properties: temperature $T_1$ , pressure $P_1$, and density $\rho_1$.
4. Our calculator will provide you with the following results:
   • Downstream Mach number or Mach number after the expansion wave $M_2$;
   • Downstream flow properties: temperature $T_2$, pressure $P_2$, and density $\rho_2$; and
   • Mach angles and Prandtl Meyer function evaluations for $M_1$ and $M_2$.

Hooray! You learned to use our calculator to find flow properties after the expansion waves. If you are curious about oblique shock waves, please check our oblique shock calculator. We are sure you will like it ;).

Now, it's time to look at an example.

1. Let us consider an upstream flow with the following properties:

   • Mach number $M_1$ = 1.5;
   • Pressure $P_1$ = 1 atm;
   • Temperature $T_1$ = 288 K;
   • Density $\rho_1$ = 1.22586 kg/m³; and
   • Deflection angle $\theta$ = 15 degrees.

2. For our example, let us assume we need all the downstream properties. Therefore, first, choose "YES" for the "Do you want flow properties ?" option. Now you can insert the inputs, and our calculator will provide you with the results right away. Click the advanced mode button to see forward and rearward Mach angles and Prandtl Meyer function evaluations. Following are the results from the calculator:

   • $M_2$ = 2.0;
   • $\nu_2$ = 26.91 degrees (advanced mode);
   • $\nu_1$ = 11.91 degrees (advanced mode);
   • Pressure $P_2$ = 0.469 atm;
   • Temperature $T_2$ = 230.0336 K;
   • Density $\rho_2$ = 0.69896 kg}/m³;
   • Forward Mach angle $\mu_1$ = 41.81 degrees (advanced mode);
   • Rearward Mach angle $\mu_2$ = 29.6874 degrees (advanced mode); and
   • Flow deflection with respect to horizontal plane = $\nu_2-\theta$ = 14.68737 degrees.

Cool! We hope now you are confident to tackle any challenges that arise when you want to deal with Prandtl Meyer expansion waves!

To find the pressure downstream of the expansion wave, follow these steps:

1. Find the downstream Prandtl Meyer function using the upstream Mach number and the deflection angle.
2. Using the result from step 1, use the Prandtl Meyer function – Mach number table or solve the Prandtl Meyer equation for downstream Mach number to obtain the downstream Mach number.
3. Calculate the total pressure using the upstream pressure and isentropic pressure ratio – Mach number table.
4. Obtain the downstream pressure by using the total pressure and the isentropic pressure ratio and the Mach number table.

The Mach angle is 41.81 degrees for Mach number 1.5. You can calculate the Mach angle by taking the arcsin of one divided by the Mach number.

The total pressure remains constant through an expansion wave. This constancy is due to the fact that there is no discontinuity in the expansion wave, unlike shock waves where discontinuity changes the total pressure.

Yes, expansion waves are isentropic. Due to the continuous nature of the expansion wave, there is no loss due to dissipation; as a result, entropy and stagnation properties remain constant. This condition makes expansion waves isentropic.