NPSH Calculator – Net Positive Suction Head
The net positive suction head calculator (NPSH) is a fantastic tool that assists you in obtaining the available NPSH of your pumping system and preventing it from cavitating.
This article will cover what NPSH is, how cavitation destroys your pump, how to calculate NPSH, and how to eliminate this problem from your system.
What is cavitation?
Cavitation is a phenomenon in which the static pressure of a liquid fluid decreases below its vapor pressure, causing it to evaporate, creating vapor bubbles. It happens in pumping systems near the surface of the pumping blades, where the blade's shape and rotation make different pressure profiles. First, let's explore the following pressure-temperature water diagram. Note if the pressure goes down (at a constant temperature), we get vapor.
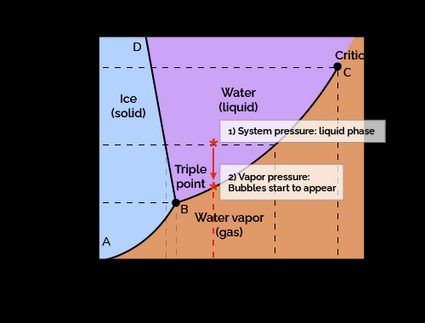
When the fluid leaves the section of low pressure and enters regions of higher pressure, it condensates. The vapor bubble experiences a volume contraction (phase liquid occupies less space than gas, as you can see in the density calculator ) that makes it burst, releasing heat, acoustic energy, and shockwaves that damage the pump internals. Again, check the image above and see what happens if fluid pressure increases at a constant temperature.
In the following two diagrams, we see the complete process.
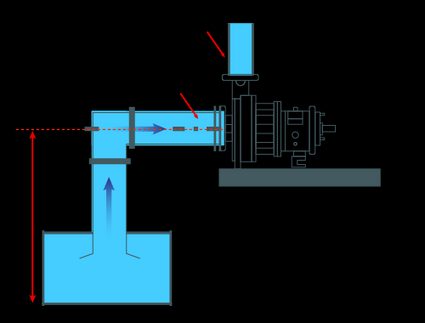
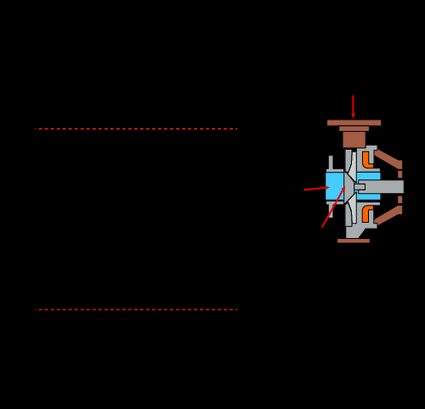
What is net positive suction head?
The net positive suction head (NPSH) of a pump refers to the difference between the suction pressure at the pump's inlet and the fluid's vapor pressure at the system temperature. See the NPSH formula per definition:
where and subscripts refer to the suction side and vapor, respectively.
Inside a pump, under normal conditions, we only have fluid in the liquid phase. However, if pressure drops to a certain value, known as vapor pressure, vapor starts to appear. Consequently, we need that differential pressure to be high enough to avoid this situation.
Manufacturers test the pumps under controlled environments to get such minimum pressure of operation and call it NPSH required.
What is the NPSH formula for avoiding cavitation?
We have already explored the NPSH formula, considering the pressure inside the pump. However, such pressure it's not practical to obtain. Consequently, we use the Bernoulli equation calculator to rearrange the formula considering other system points. See the next diagram:

Assuming this is an open reservoir, represents the friction loss in pipe fittings and to be the height between the water level and pump level. Then, we have the following NPSH formula (if you are worried about remembering it, you can try our Net positive suction head calculator):
where:
- — Represents the pressure at the surface of the liquid. If the reservoir is open, you will only have atmospheric pressure ; otherwise, you have to consider absolute reservoir pressure .
- — Indicates the vapor pressure at the pumping system temperature.
- and — Represent fluid density at the pumping system temperature and acceleration due to gravity.
- — Consider the height between the liquid surface and pump inlet level. Multiply this value by if the tank is above the pump level. You can learn more about the effect of the water height in our hydrostatic pressure calculator.
- — Reflects the fluid head loss due to friction in the suction pipe.
The above formula represents the NPSH in our system, also known as the "NPSH available." To avoid cavitation, our goal is to keep "NPSH available" greater than "NPSH required", which the manufacturer provides.
How to calculate the NPSH available — Real life example
In this section, we will explain a real-life NPSH calculation example. Imagine you want to pump water that is 1 meter below the pump level. Its temperature is 20 °C. The reservoir is open to the atmosphere, and we assume a friction loss of 1.7 meters.
Introduce the system values in our net positive suction head calculator or follow the next steps:
-
In your reservoir, because it is open, you have = . Note .
-
Get the distance between the pump and the liquid's surface: . In this case .
-
Obtain the vapor pressure for the system's temperature: 20 °C. . Also, its density: . Meanwhile, gravity is always .
-
Calculate all friction loss in the suction pipe. In this case, .
-
Finally, solve the NPSH formula:
- We obtain 7.41m, the NPSH available for the system. Now, as long as your NPSH available is above the NPSH required provided by the manufacturer at your system flow rate, you will not have cavitation.
How to reduce risk of cavitation?
First, we need to remember what cavitation is. Then, we notice we must increase the NPSH available in our system above the NPSH required. See the following considerations to achieve it:
-
Reducing the distance between your pump and your fluid reservoir will increase the NPSH available calculation. However, this method only applies if the pump is above the liquid tank.
-
Eliminate unnecessary fitting: pipes, elbows, valves, etc., in your suction line. It reduces friction losses, thus increasing the NPSH available.
-
Reduce the temperature of your pump and your pumping system. Accordingly to the NPSH formula, it will reduce , thus increasing NPSH in the pump.
-
Reduce motor/pump speed since it will decrease the pressure drop that the fluid experiences through the impeller. Higher velocities create more pressure drop, hence a higher risk of cavitation.
You can directly try the first three recommendations in our net positive suction head calculator by simulating an example and modifying the following values: the distance between the pump and fluid reservoir, friction loss, and vapor pressure.
FAQs
What is the net positive suction head?
Net positive suction head (NPSH) is the difference between the suction pressure at the inlet of a pump and the pressure at which the fluid starts to vaporize (vapor pressure). Engineers use it to design pumping systems to avoid cavitation.
What causes cavitation?
The main reason for cavitation is low pressure at the inlet of a pump because when it experiences further pressure decrease when passing through the blades, it starts evaporating. That is why you want higher pressure at the inlet, conversely, a higher net positive suction head (NPSH).
How to avoid cavitation?
You mainly need to increase the NPSH available above the NPSH required by the manufacturer. Here are three proven methods to avoid cavitation:
-
Reduce the distance between your pump and your fluid tank in case the pump is above the liquid tank.
-
Eliminate unnecessary fitting: pipes, elbows, valves, etc., in your suction line. It reduces friction losses.
-
Clean your water from any debris.
How do you calculate the NPSH available?
Try our Net positive suction head calculator or:
-
In your reservoir, get fluid surface pressure: Psurface.
-
Get the distance between the pump and liquid surface: Z. If the tank is above the pump, multiply this value by -1.
-
Obtain the vapor pressure for the system's temperature: Pvapor. Also, its density is ρ. Note that g represents gravity.
-
Calculate all friction loss in the suction pipe: Hloss.
-
Solve: ((Psurface - Pvapor)/ρ × g) − Z − Hloss, and you will have NPSH available.