Low Pass Filter Calculator

Welcome to Omni's low pass filter calculator. Whether you're designing an entire sound system complete with a bass boost, or just want to remove high-frequency noise, the low-pass filter calculator can help you create the perfect low-pass filter circuit for your needs. Read on to learn:

• What a low-pass filter is;
• The difference between passive and active low-pass filters; and
• Whether inductors (that offer inductive reactance) can be used for low-pass filters.

Using the low-pass filter calculator is easy! Here's how:

1. Select the filter type you're designing. Based on this choice, the low-pass filter calculator can magically transform into an RC low-pass filter calculator, an op-amp low-pass filter calculator, and others. We offer the following filter types:

   • An RC low-pass filter;
   • An RL low-pass filter;
   • An non-inverting op-amp low-pass filter; and
   • An inverting op-amp low-pass filter.

2. Input the values you are using. The passive (RC and RL) filters allow component values and the desired cutoff frequency. To the active (op-amp) filters, you can also add a gain to your AC signal. Read on if you want to learn how they work!

A low-pass filter is an electronic circuit that removes higher-frequency components from a given AC signal. In other words, it blocks high frequencies and lets low frequencies pass — hence the name "low-pass filter".

Let's illustrate a low-pass filter's frequency response (a fancy word for how a filter amplifies or dampens signals of certain frequencies). Take a look at the typical Bode plot for a low-pass filter below:

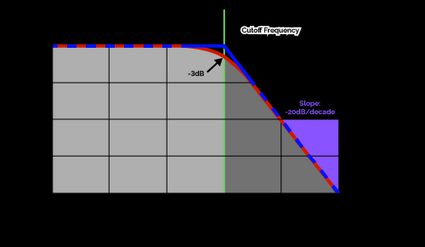
In the graphic above, we can see that a low-pass filter's frequency response is relatively flat up to $f_c$, after which it descends quickly. That point $f_c$ is called the cutoff frequency and it's the defining parameter of a low-pass filter.

Past the cutoff frequency, the filter's frequency response drops at a slope of 20 decibels per decade — or, equivalently, the amplitude of a signal passing through the filter decreases by a factor of 10 for every tenfold increase in the signal's frequency.

When dealing with signals containing more than one frequency, a low-pass filter will remove the high-frequency components while leaving low-frequency components untouched. For audio systems, this would typically mean the treble is dampened, and the bass is seemingly amplified.

While all low-pass filters perform the same function, many different low-pass filter circuits exist. They are split into two categories, passive and active, and this dichotomy can be categorized further:

• Passive low-pass filters are built with only the three linear passive components: the resistor, the capacitor, and the inductor. They include:
  • RC low-pass filters; and
  • RL low-pass filters.
• Active low-pass filters can be built with active components, most notably the operational amplifier (or op-amp). They include:
  • Inverting op-amp low-pass filters; and
  • Non-inverting op-amp low-pass filters.

The RC low-pass filter consists of a resistor (with resistance $R$) and a capacitor (with capacitance $C$) in the configuration shown below:

The RC low-pass filter is probably the most well-known passive low-pass filter. It is simple to design and build thanks to the simple formula for its cutoff frequency $f_c$:

The RC low-pass filter takes advantage of the reactive properties of the capacitor, whose impedance $Z_C$ decreases as the signal frequency $f$ increases:

Higher frequencies can easily pass through the capacitor and skip the load at $v_\text{out}$; lower frequencies are blocked from flowing through the capacitor and must instead travel through the output terminals. In this way, lower frequencies are delivered to the load, and higher frequencies are filtered out.

We haven't seen any inductors yet, but don't worry — inductors can be used for a low-pass filter just as easily as capacitors and resistors! Similar to the RC filter, the RL low-pass filter is another passive filter, and is constructed with a resistor $R$ and an inductor $L$ in this configuration:

Its cutoff frequency can be determined with this formula:

Inductors behave in the opposite way to capacitors — their impedance $Z_L$ grows with the frequency $f$ of the signal it's conducting:

As a result, the inductor in the RL low-pass filter blocks higher frequencies from ever reaching $v_\text{out}$, while allowing lower frequencies to pass through the inductor and reach the output.

The inverting op-amp low-pass filter is an active filter, meaning it doesn't use just passive components (resistors, capacitors, and inductors). This particular filter incorporates an operational amplifier (op-amp) that feeds back into itself with the feedback resistor $R_f$ and capacitor $C$. It's designed as follows:

Lucky for us, the formula for the cutoff frequency is simple:

Because op-amps are powered by an external voltage source that is independent of the input signal, the inverting op-amp low-pass filter introduces a gain $G$ by which the input signal $v_\text{in}$ will be multiplied to obtain $v_\text{out}$:

It's important to note that the inverting op-amp low-pass filter's gain $G$ is negative. Therefore, your output signal $v_\text{out}$ will be flipped to be exactly 180° out of phase with the input signal $v_\text{in}$ — that's why it's called an "inverting filter". For some circuits (like audio systems) this effect doesn't matter much (as speakers don't care about polarity) but in other applications, the flip must be kept in mind. If you want to avoid this flip, then jump on over to the section on NON-inverting op-amp low-pass filters.

The non-inverting op-amp low-pass filter doesn't flip the signal like the inverting op-amp filter does — its output $v_\text{out}$ retains the polarity of its input $v_\text{in}$.

The formula for its cutoff frequency is:

As an active filter, the non-inverting op-amp low-pass filter also introduces a gain $G$:

Because of the $1$ in $G = 1 + R_f/R_g$, the gain will always be at least $1$, i.e. $G\ge1$. So, if you were planning on reducing the amplitude of your signal with $G < 1$, you might want to consider the inverting op-amp low-pass filter instead.