Knudsen Number Calculator

Our Knudsen number calculator is a simple tool that helps you compute the Knudsen number – one of the dimensionless characteristic numbers in fluid mechanics (see prandtl number calculator). Its value serves as the primary criterion for the applicability of fluid mechanics equations. In the following text, we will explain what the Knudsen number is and how you can calculate it using the Knudsen number definition.

The Knudsen number is mainly used in diluted gases, e.g., high vacuums. Read on to find out what is the classification of vacuum ranges and how it influences the mean free path of particles. Keep reading to learn more about the Knudsen number.

Fluid dynamics is a branch of physics that describes the flow of fluids – liquids and gases. Generally, there are two formulations of fluid dynamics that can be used:

• Statistical mechanics considers the microscopic structure of matter – every particle separately. This approach is based on statistical methods, probability theory, and microscopic physical laws. Our ideal gas law calculator and particles velocity calculator were derived from the statistical mechanics. Check them out!

• Continuum mechanics, as opposed to statistical mechanics, omits the description at the microscopic level. It ignores the fact that matter is made of atoms. Examples are the Bernoulli equation and Stoke's law calculator (see Stokes' law calculator).

The Knudsen number helps determine which of the above formulations of fluid dynamics should be applied in the specific situation. If the mean free path of the molecules of fluid is larger than the size of the chamber or the pipe, then the continuum assumption of fluid mechanics is no longer a good approximation. We have to use statistical mechanics.

In most cases, the Knudsen number is very low since the average free path of air molecules under normal conditions is about 6.21 × 10^-8 m. Hence, we can use continuum mechanics approach. However, the situation is different in highly rarefied fluids, e.g., outer space or the Earth's exosphere, where the density of molecules is too low for them to collide with each other (like in gases). The same is true for gases subject to very low pressures, i.e., in high vacuum.

Knudsen number is a dimensionless quantity that depends on the mean free path of the particle and the characteristic linear dimension. Our Knudsen number calculator uses below Knudsen number formula:

where:

• $\rm Kn$ – Knudsen number (dimensionless);
• $\lambda$ – Mean free path (expressed in length units); and
• $L$ – Characteristic linear dimension (expressed in length units).

Characteristic linear dimension $L$ (or characteristic length) is a matter of convention. By definition, it determines the minimum scale of length at which significant differences in macroscopic flow parameters can be observed. For example, for flow through the pipe, you can take pipe's diameter (or radius) as $L$. It should be noted that different authors may use slightly different definitions of $L$, especially for flows in complex geometries. Therefore characteristic linear dimension has no unambiguously determined value.

The importance of the Knudsen number is that when $\small \rm Kn \ll 1$, the fluid behaves as a continuum fluid. On the other hand, when $\small \rm Kn \gg 1$, then statistical mechanics should be applied.

The Knudsen number is an essential parameter in the vacuum technology. As can be seen in the figure below, we can distinguish between various types of fluid flow.

When the Knudsen number is small (low vacuum), then there are frequent collisions between gas molecules, but less frequent ones with the walls of the pipe.

In the case of a high Knudsen number (high vacuum), there are almost no interactions between particles, and thus the particles collide only with the walls.

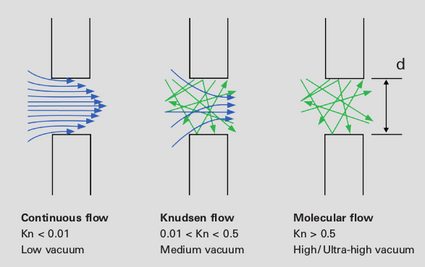
In the following table, you will find the classification of vacuum ranges for air at room temperature (300 K). If you assume that the characteristic length $L$ equals the diameter of the pipe (e.g., 10 cm), you will have everything you need to calculate Knudsen number of the airflow.

We encourage you to use our Knudsen number calculator and check whether the flow is continuous or molecular (statistical)!