Hoop Stress Calculator

The hoop stress calculator determines the stresses acting on a thin-walled pressure vessel. Pressure vessels are specially designed containers used to hold fluids at a different pressure than ambient ones. Due to high internal pressure, the parameters like hoop stress and longitudinal stress become crucial when designing these containers.

Knowledge of these stresses is helpful in designing the riveted or welded joints on the body. Various pressure vessels include boilers, water tanks, petrol tanks, gas cylinders, spray cans, fire extinguishers, pipes, etc. Read on to understand what hoop stress is, longitudinal stress in a cylinder, and more.

A pressure vessel is manufactured using rolled-up sheets welded or riveted together. In some cases, it is also forged. The manufacturing process depends on various factors like application and required strength.

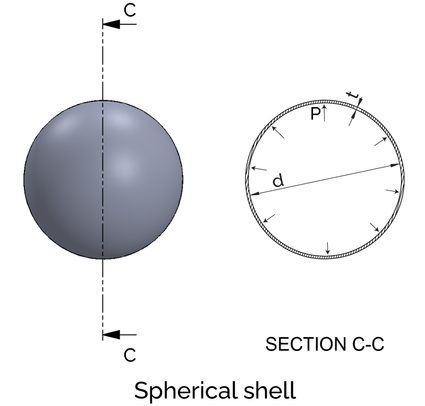
A pressure vessel design includes an estimation of the stresses that can cause failure. The shapes for the pressure vessel calculations are simplified as a cylinder or spherical in most cases. The shells are classified as either thick or thin based on their dimensions. If a shell's wall thickness is not greater than one-tenth of the radius, it is regarded as a thin shell.

Consider a thin-walled pressure vessel. When a shell is subjected to a large amount of internal pressure, tensile stresses act along both directions. The stress acting along the tangential direction to the circumference of a sphere or cylindrical shell is known as circumferential stress or hoop stress. In a cylindrical shell, the stress acting along the direction of the length of the cylinder is known as longitudinal stress.

These stresses are vital parameters when it comes to pressure vessel design. Therefore, the maximum permissible stress in the material must not exceed either the circumferential or hoop stress. The failure from hoop stress results in rupturing of a cylindrical shell in two cylinders, whereas the excess longitudinal stress in the cylinder splits the cylinder into two troughs.

For a cylindrical shell having diameter $d$ and thickness $t$, the circumferential or hoop stress $\sigma_{\mathrm{h}}$ is given by the hoop stress equation:

where $p$ is internal pressure. The large cylindrical shells are manufactured with joints, and when the efficiency of the joints is taken into consideration, the circumferential stress equation becomes:

where $\eta_\mathrm{t}$ is the efficiency of longitudinal joints because the forces are acting along the longitudinal section. Similarly, the longitudinal stress, considering circumferential joint efficiency, $\eta_\mathrm{c}$ is:

Now that we know the hoop stress, one can also estimate the ratio of longitudinal stress to hoop stress, which is $0.5$. The hoop stress acting on a cylindrical shell is double the longitudinal stress, considering ideal efficiency.

For a sphere, the hoop stress of a thin walled pressure vessel is also calculated using similar principle; however, the stress acting on the shell is only of one type, i.e., the hoop stress. The hoop stress formula for a spherical shell is:

where $\eta$ is the efficiency of joints.

Due to the extreme operating conditions and internal pressure, the shell tends to expand or contract, i.e., the dimensions change due to the stresses. The change in dimensions is a function of material properties as well as the stresses.

Consider a shell of made a material whose Young's modulus is $E$ and Poisson's ratio, $μ$ (any doubts on those concepts? Our Young's modulus calculator and Poisson's ratio calculator are here to help you!). A cylinder has two main dimensions – length and diameter, which would change due to internal pressure. The change in diameter $\delta d$ is:

The change in length $\delta l$ is written as:

Interestingly, upon rearranging the above equations, the strain $\varepsilon$ is a function of stress (either hoop or longitudinal) and material constants. For instance:

As the dimensions of the shell increases, the volume is also affected, it is given by the equation:

Similarly, the change in dimensions for the spherical shell can be estimated using the equations:

And:

Now that you know what hoop stress is and its equation. Let's go through the steps to calculate the stresses using this hoop stress calculator.

1. Select the shape of the shell, either Sphere or Cylinder.

2. Enter the radius $r$ or diameter $d$ of the shell.

3. Fill in the thickness of the shell, $t$.

4. The calculator returns the thickness to diameter ratio.

5. Enter the internal pressure on the walls of the shell, $p$.

6. Insert Young's modulus $E$ and Poisson's ratio $μ$ for the shell material.

7. The hoop stress calculator will return the respective stresses, including shear stress in pressure vessels and changes in dimensions.

Estimate the hoop stress in a water tank built using riveted joints of efficiency $0.75$ and having an internal pressure of $1.5\ \mathrm{MPa}$. Take diameter and thickness of the shell as $3\ \mathrm{m}$ and $16.667\ \mathrm{mm}$ respectively.
To find the hoop stress in the spherical tank:

1. Select the shape of the shell as Sphere.

2. Enter the diameter of the shell, $d = 3\ \mathrm{m}$.

3. Input the thickness of the shell, $t = 16.667\ \mathrm{mm}$.

4. Enter the internal pressure on the walls of the shell, $p = 1.5\ \mathrm{MPa}$.

5. Click on "Joint efficiency" and set it to $0.75$.

6. The hoop stress calculator then uses the circumference stress equation:

You can follow similar steps if you wonder how to calculate hoop stress in a pipe by setting the shape to Cylinder, or for any other pressure vessel calculations.