Last updated: Mar 14, 2024

Contact Lens Vertex Calculator

Q: What is BVD 12 on eye prescription?

BVD stands for back vertex distance , the distance from the back surface of the lens to your cornea. BVD 12 mm means the refraction prescription was measured at a 12 mm vertex distance. Read more

Q: What lens power compensates a +8.0 D lens moved 4 mm away?

You require a lens of +7.75 D to compensate for the vertex change of 4 mm away from your eye. To arrive at this answer, follow these steps: Since the lens is moved away from your eye , the vertex change is negative. Multiply the old lens power by the vertex change in meters: +8.0 × -4/1000 = -0.032 Subtract this result from 1 : 1 − (-0.032) = 1.032 Divide the old lens power by this result to get the vertex-compensated lens power: +8.0/1.032 ≈ 7.75 D To verify this result, use our contact lens vertex calculator . Read more

Table of contents

Lens power, perceived power, and vertex distance Formula to calculate vertex compensation Contact lens back vertex calculation for spherical lenses Contact lens vertex calculation for toric lenses Using this contact lens vertex calculator FAQs

Our contact lens vertex calculator is the perfect tool for you if you're switching your eyeglasses for a pair of contacts. This simple tool will help you determine the power of your contact lens from the power of your eyeglasses! You can use our contact lens vertex calculator for toric and spherical lens.

But why can't you choose a contact lens with the same power as your specs? What is vertex, and how does vertex distance affect contact lens calculation? How do we calculate vertex compensation for toric and spherical lenses? We shall learn all this in the following article, so bear with us!

If you want to read up on how lenses work before getting into this topic, we encourage you to go through our thin lens equation calculator first.

Lens power, perceived power, and vertex distance

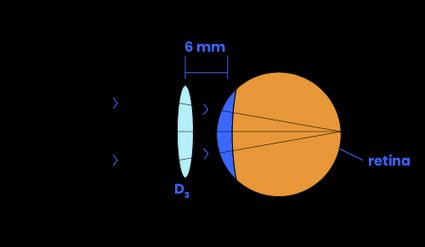
The lens in your eyeglasses helps you see better by refracting the light from an object onto your retina. The power of this lens is the inverse of its focal length.

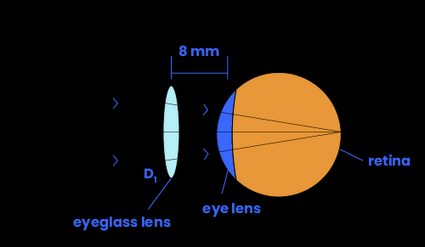
An eyeglass at regular distance focusing an image onto the retina.

The eyeglass frame holds this lens at a distance from your eye such that the focal length of the eyeglass-eye optical system lines up with your retina. We call this distance from your eye to the eyeglass the vertex. Usually, it is in the range of 12-14 mm.

🔎 A positive power lens converges light while a negative power lens diverges it.

Suppose you want to switch to a different frame that moves the lens some distance. If you keep the same lens, its power will not change, nor will your eyeglass-eye system's focal length. But this presents a problem — the light is no longer focused on your retina, so your vision is blurry!

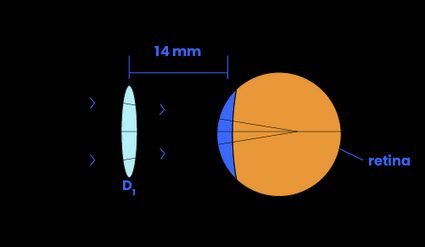
Eyeglass moved a distance away from the eye refracts the image before the retina.

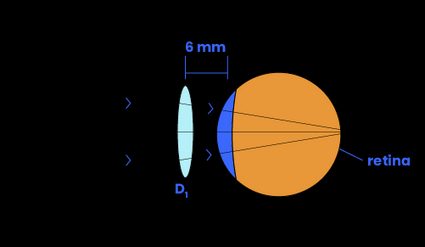
Eyeglass moved a distance towards from the eye refracts the image beyond the retina. — Using the same eyeglass at a different distance from the eye fails to refract the image onto the retina.

Although the lens power remains the same, your brain perceives a loss (for a positive power lens) in power. If the lens were moved closer to the eye instead, the light wouldn't be focused on your retina, and you would perceive a gain in power (for a positive power lens). Note that the opposite is valid for a negative-powered lens.

In other words, when the vertex distance changes, you can no longer use the same lens in your eyeglasses — you must compensate for the new vertex! We will find a new lens power that will work for this vertex so that your brain's perceived power remains unchanged! You don't need a new prescription because your eye power did not change, and we have a formula to calculate vertex compensation.

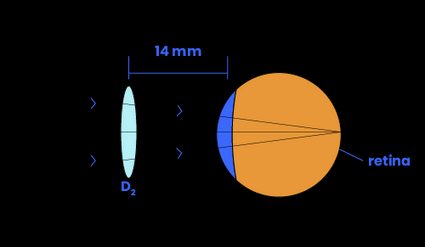
A vertex compensated lens focuses the image onto the retina.

Formula to calculate vertex compensation

The power of a lens is given by:

F = \frac{1}{f}

where:

$F$ — The lens power in dioptres (D); and
$f$ — The focal length in meters (m).

🔎 The focal length must be in meters when calculating lens power. For a deeper dive into focal length, visit our focal length calculator.

The formula for calculating vertex compensation is:

F_c = \frac{F_o}{1-d \cdot F_o}

where:

$F_c$ — Power of the vertex compensated lens;
$F_o$ — Original lens power; and
$d$ — Change in the vertex distance in meters.

Note that the change in vertex distance is given by:

d = d_i - d_f

where:

$d_i$ — Initial vertex distance in meters; and
$d_f$ — Final vertex distance in meters.

So, while the initial and final vertex distance must always be positive, the change in vertex distance can be either positive or negative based on whether the lens is moved closer or away from its initial position with respect to the eye.

When calculating vertex adjustment for contact lenses, the final vertex distance is zero because the lens rests on the cornea. So in spectacle to contact lens vertex calculation, the $d$ is always positive.

Contact lens back vertex calculation for spherical lenses

Spherical lenses have spherical curvature. The power of the lens is uniform in all directions. Calculating contact lens vertex distance for a spherical lens is simple. We follow the vertex compensation formula introduced earlier, with some customization:

F_{\rm C} = \frac{F_{\rm Sp}}{1-d \cdot F_{\rm Sp}}

$F_{\rm C}$ — Contact lens power; and
$F_{\rm Sp}$ — Spectacle lens power.

Note that the change in vertex distance $d$ , given by:

\begin{align*} d &= d_i - d_f\\ &= d_{\rm Sp} - d_{\rm C}\\ &= d_{\rm Sp} - 0\\ d &= d_{\rm Sp} \end{align*}

where:

$d_{\rm Sp}$ — Spectacle vertex distance; and
$d_{\rm C}$ — Contact lens vertex distance, equal to 0.

We will understand the problem better with an example. Say our friend Mila uses eyeglasses with a +8 D lens for her right eye and a +6.5 D lens for her left. She decided to switch to contact lenses. If the spectacles she wore were 10 mm away from her eye, what should be the power of her contact lenses?

Let us start by calculating contact lens vertex distance. Since she is switching to contacts, her vertex distance change is:

\begin{align*} d &= d_{\rm Sp} - d_{\rm C} = 10 \text{ mm} - 0 \text{ mm}\\ d &= 10 \text{ mm} = 0.01 \text{ m}\\ \end{align*}

Now, we can calculate contact lens back vertex compensation for her right eye.

\begin{align*} F_{\rm C} &= \frac{F_{\rm Sp}}{1-d \cdot F_{\rm Sp}}\\[1em] &= \frac{8}{1-0.01 \cdot8} = \frac{8}{1-0.08}\\[1em] &= \frac{8}{0.92} \equiv 8.6957\\[1em] F_{\rm C} &\approx 8.7 \end{align*}

So, for Mila to have the same experience as she had with her eyeglasses, she needs a +8.7 D contact lens for her right eye.

Similarly, calculate contact lens vertex adjustment for her left eye:

\begin{align*} F_{\rm C} &= \frac{F_{\rm Sp}}{1-d \cdot F_{\rm Sp}}\\[1em] &= \frac{6.5}{1-0.01 \cdot6.5} = \frac{6.5}{1-0.065}\\[1em] &= \frac{6.5}{0.935} \equiv 6.952\\[1em] F_{\rm C} &\approx 6.95 \end{align*}

There you go! Mila needs a pair of contacts with +8.7 D for her right eye and +6.95 for her left, and she will be set!

🔎 If you're curious how one designs a lens to a specific power or focal length, visit our lens maker equation calculator.

Contact lens vertex calculation for toric lenses

Toric lenses have two different curvatures — spherical and cylindrical curvatures — along two orthogonal meridians. Toric refers to a section of a torus (think donut shape!). Due to these two separate curvatures, the lens has different powers along the two meridians. Also known as sphero-cylindrical lenses, they are used to treat astigmatism.

Calculating contact lens vertex adjustment for a toric lens is more complicated. The spectacle prescription includes three items:

The spherical power.
The cylindrical power.
The angle (in degrees) that indicates the orientation of the two meridians to the horizontal.

It's a bit tricky, but we can break it down with an example. Suppose your friend Reggie has astigmatism, and he wants to try contacts. His spectacle prescription is:

	Sphere	Cylinder	Axis
Right:	-8.00 D	-4.25D	45
Left:	-8.75 D	-5.00 D	45

The back vertex distance is 14 mm. Since Reggie wants contact lenses, we will calculate the spectacle to contact lens vertex compensation for him, beginning with the right eye:

Start with the spherical power. This power is along one lens meridian. We convert this the same way we calculated vertex compensation for the spherical lens:

\qquad \begin{align*} F_{\rm C} &= \frac{F_{\rm Sp}}{1-d \cdot F_{\rm Sp}}\\[1em] &= \frac{-8}{1-0.014 \cdot-8} \\[1em]&= \frac{-8}{1+0.112}\\[1em] &= \frac{-8}{1.112} \approx -7.1942\\[1em] F_{\rm C} & \equiv -7.19 \text{ D} \end{align*}

Next, we move to the next meridian. The power along this meridian is the sum of the spherical and cylindrical powers:

\qquad \begin{split} F_{ \rm Sp} &= -8 + (-4.25) \\&= -12.25 \text{ D} \end{split}

The two meridians of the old lens, with the horizontal meridian for the spherical power and vertical for the "cumulative" power.

Now, we calculate the contact lens vertex adjustment for this cumulative power along the second meridian:

\qquad \begin{align*} F_{\rm C} &= \frac{F_{\rm Sp}}{1-d \cdot F_{\rm Sp}}\\[1em] &= \frac{-12.25}{1-0.014 \cdot-12.25} \\[1em]&= \frac{-12.25}{1+0.1715}\\[1em] &= \frac{-12.25}{1.1715} \approx -10.4567\\[1em] F_{\rm C} & \equiv -10.46\text{ D} \end{align*}

The two meridians of the vertex compensated lens, with the horizontal meridian for the spherical power and vertical for the "cumulative" power.

This is the vertex compensated (or corrected) cumulative power along the second meridian. To obtain the cylindrical power, subtract the compensated spherical power we calculated in step 1.

\quad\ \ \begin{split} F_{\rm cylinder} &= -10.46 - (-7.19) \\&= -3.27 \text{ D} \end{split}

The axis remains unchanged when calculating toric contact lens vertex compensation.

Repeating these steps for the left eye gives the vertex compensated powers as -7.80 -3.74 × 45. Let's summarize the results in a table.

	Sphere	Cylinder	Axis
Right:	-7.19 D	-3.27 D	45
Left:	-7.80 D	-3.74 D	45

Using this contact lens vertex calculator

Our contact lens vertex calculator is very simple to use:

Select whether the lens is spherical or sphero-cylindrical (toric).
Provide the corresponding lens powers for both the eyes. The axis remains unaltered during vertex compensation calculation, so you need not provide it.
Enter the change in vertex distance. You can do it in two ways:
- Directly give a value for the change in vertex distance; or
- Enter the initial and final vertex distances. Since the final vertex distance for a contact lens is zero, this value is set to 0 by default.
Our calculator will instantly determine the vertex-compensated lens powers for your contact lenses!

Note: You can round the values calculated above to the nearest 0.25 D to obtain the closest lens specification available in the market. Lenses come with a tolerance of ±0.13 D anyway, so the rounding will not affect your vision quality.

🔎 If you want to calculate vertex compensation for a different lens, not a contact lens (i.e., you're moving your spectacle lens toward or away from your eyes for some reason), enter a non-zero final vertex distance in step 3, and our calculator will yield the results you seek!

FAQs

What is BVD 12 on eye prescription?

BVD stands for back vertex distance, the distance from the back surface of the lens to your cornea. BVD 12 mm means the refraction prescription was measured at a 12 mm vertex distance.

What is the vertex of a contact lens?

The vertex distance is the distance between the lens and your eye. The vertex distance of a contact lens is zero since a contact lens rests on top of your cornea.

How do you calculate vertex compensation for toric lenses?

To calculate vertex adjustment for toric contact lens, follow these steps:

Convert the spherical power using the vertex compensation formula:

F_{compensated, sphere} = F_old/(1 − d⋅F_old)

where d is the vertex change.
Add the spherical and cylindrical powers to obtain the cumulative power in the second meridian:

F_{specs, 2meridian} = F_{specs, sphere} + F_{specs, cylinder}
Substitute F_{specs, 2meridian} as F_old in the formula in step 1 to obtain F_{compensated, 2meridian}.
Subtract the compensated spherical power from the compensated second meridian power to obtain the compensated cylindrical power:

F_{compensated, cylinder} = F_{compensated, 2meridian} + F_{compensated, sphere}.

What happens when a plus lens is moved closer to the eye?

When a plus lens (converging lens) is moved closer to the eye, it loses perceived power because the new focal point falls behind the retina. Conversely, when a plus lens is moved away from the eye, it gains perceived power because the new focal point lies in front of the retina.

What lens power compensates a +8.0 D lens moved 4 mm away?

You require a lens of +7.75 D to compensate for the vertex change of 4 mm away from your eye. To arrive at this answer, follow these steps:

Since the lens is moved away from your eye, the vertex change is negative.
Multiply the old lens power by the vertex change in meters:

+8.0 × -4/1000 = -0.032
Subtract this result from 1:

1 − (-0.032) = 1.032
Divide the old lens power by this result to get the vertex-compensated lens power:

+8.0/1.032 ≈ 7.75 D

To verify this result, use our contact lens vertex calculator.