Bulk Modulus Calculator
This tool calculates the bulk modulus of an object, given its initial volume, the pressure applied to it (bulk stress), and the volume change caused by that stress.
Bulk modulus is a property relevant to many physical phenomena. For example, for sound waves traveling through a fluid medium, the speed of sound is proportional to the square root of the bulk modulus. In the study of isotropic solid materials, the bulk modulus is tightly related to Poisson's ratio, a crucial property in the strain analysis of materials (look at this formula in the FAQ section and compute that property with the Poisson's ratio calculator).
This tool uses the widely known bulk modulus formula, which relates bulk modulus to bulk stress and strain. The following sections show how to calculate the bulk modulus utilizing that formula and give some common values, such as the bulk modulus for water, lithium, etc.
How to calculate the bulk modulus with the formula
With this formula, you calculate the bulk modulus:
B = -ΔP/(ΔV/V₀)
where:
- B — Material's bulk's modulus;
- V₀ — Initial volume of the material;
- ΔP — Additional pressure applied to the material, known as pressure stress; and
- ΔV — Volume change caused by the pressure.
The ΔV/V₀ term is known as bulk strain, which indicates the fractional or percentual volume change caused by the pressure stress.
The following image lets us better understand the bulk modulus concept.
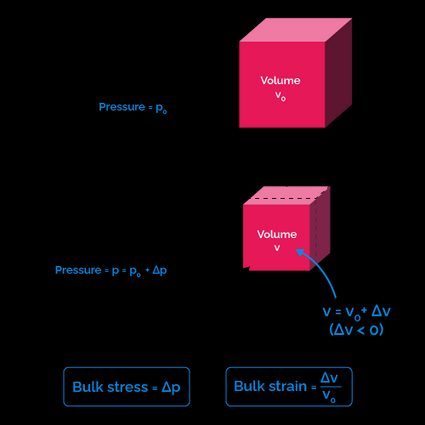
Important considerations about the bulk modulus formula
- Bulk modulus indicates how much pressure we need to apply to a material to cause deformation.
- The bulk modulus formula applies to materials that obey Hook's law, as this law is the basis for treating bulk stress and strain as linearly related quantities.
- The bulk modulus for lithium, water, and other solids and liquids is considered constant (especially for small pressure changes). However, the bulk modulus of gases depends on the initial pressure P₀.
- The bulk modulus is also related to Poisson's ratio and Young's modulus (which you can calculate using this Young's modulus calculator). In the FAQ section, we show the equation.
Bulk modulus for lithium, water, and other materials
The following is a list of typical values of bulk modulus:
- Water: 2.1 GPa (300,000 psi).
- Lithium 11 GPa (1,595,415 psi).
- Aluminum: 75 GPa (10,877,828 psi).
- Silicone rubber: 2 GPa (290,075 psi).
- Steel: 160 GPa (23,206,032 psi).
Now, let's see a bulk modulus calculation example.
Bulk modulus calculation example
A hydraulic press operates at 21 × 10⁶ Pa with 0.001155 m³ volume. The oil inside has a bulk modulus of 5 × 10⁹ Pa. Suppose you're interested in knowing the volume change due to the applied pressure.
Follow these steps to calculate it:
- In the bulk modulus formula, solve for ΔV:
- In this case, ΔP = 21 × 10⁶ Pa, V₀ = 0.001155 m³ and B = 5 × 10⁹ Pa. Input those values in the formula:
- That's it. You can also use our calculator and check the results of this bulk modulus calculation example.
FAQs
How do I calculate bulk modulus from Young's modulus?
To calculate the bulk modulus from Young's modulus, use the formula B = E / 3(1 - 2ν), where:
B— Material's bulk's modulus;E— Young's modulus of the material; andν— Poisson's ratio of the material.
Take into account that this formula only applies to isotropic solid materials.
What is the bulk modulus of air?
The isothermal bulk modulus of air is 101 kPa, while its adiabatic bulk modulus is 142 kPa.
Isothermal bulk modulus corresponds to compression processes with a constant object temperature. In contrast, the adiabatic bulk modulus refers to the absence of heat or mass transfer to that object during compression.
Can bulk modulus be negative?
No, bulk modulus can't be negative. The minus sign in the bulk modulus equation B = -ΔP/(ΔV/V₀) contrasts the invariably negative sign of the volume decrease ΔV. The multiplication of those negative numbers causes a positive bulk modulus result.
How to calculate the bulk stress in a solid?
To calculate the bulk stress (ΔP) in a solid, use the formula ΔP = -B(ΔV/V₀) or follow these steps:
- Divide the volume change by the initial volume
- Multiply the result by the bulk modulus.
- Change the sign of the previous result, or multiply it by -1.
- That's it. You can also use our bulk modulus calculator to get the result.