Archimedes' Principle Calculator

Omni's Archimedes' principle calculator helps you understand the concept of buoyancy. You can also use it to determine objects' densities and changes in mass and weight when they are submerged in a fluid.

Have you ever wondered why certain objects float and others sink? If you have, you have come to the right place.

Continue reading this article to learn about Archimedes' principle and his formula. You will also find examples of buoyancy force calculations and some interesting applications of Archimedes' principle.

Let us first start with learning what Archimedes' principle is.

When we immerse an object in any fluid, there is a net upward force on the object. This upward force is called the buoyant force or buoyancy.

The origin of the buoyant force lies in the fact that the pressure increases with an increase in depth in a fluid (remember the hydrostatic pressure equation). Therefore, the upward force applied by the fluid to the bottom of the object is greater than the downward force applied to the top of the object. Check out our dedicated tool to learn more about buoyancy and perform buoyancy experiments at home.

According to Archimedes' principle, when an object is partially or wholly immersed in a fluid, it displaces some of the fluid. The buoyant force acting on the object is equal to the weight of the fluid displaced by it.

To understand what the principle means, let us try to derive a formula for the Archimedes principle.

Let us consider an object of height $h-x$ and mass $M$ immersed in a fluid of density $\rho$ (see figure 1). If $a$ is the cross-sectional area of its top and bottom face, we can write expressions for the vertically downward ($F_1$) and upward force ($F_2$) on the object as:

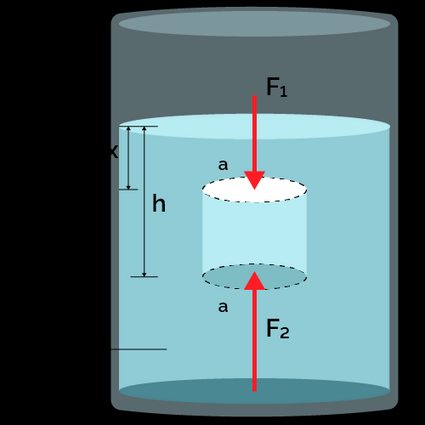
where:

• $p_1 = x \rho g$ – Pressure on the top face of the object;
• $p_2 = h \rho g$ – Pressure on the bottom face of the object;
• $x$ – Depth of the top surface of the object in the fluid; and
• $h$ – Depth of the bottom surface of the object in the fluid.

Since $h>x$, we note that $F_2 > F_1$. The net upward force or buoyant force acting on the object is:

Where $V$ is the volume of the object, and it is equal to the volume of the displaced fluid $V_{fl}$.

If $m$ is the mass of the displaced fluid, we can rewrite the above equation as:

In other words, the buoyant force acting on the object is equal to the weight of the fluid displaced by the object.

Since the true weight of the object is $W_{obj} = M g$, and the upward force on it is $F_B= m g$, the observed weight of the object in the fluid is (see figure 2):

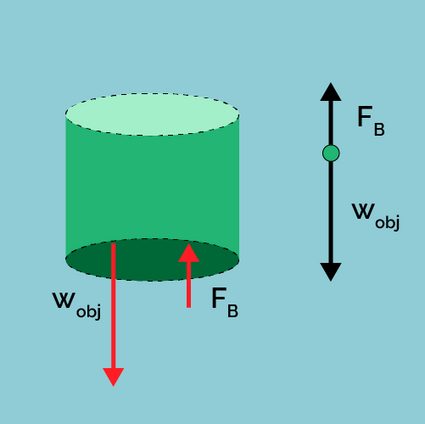
This means that when an object is immersed in a fluid, its observed weight becomes less than its true weight by an amount equal to the weight of the fluid displaced by the object (to know more, check out the immersed weight calculator.

Now, if the weight of the fluid displaced by the immersed body is greater than or equal to the body's weight, the body will float. Otherwise, it will sink. This is also known as the law of floatation.

Another fact that follows from the law mentioned above is that if the average density of an object is less than that of the fluid it is immersed in, it will float. In contrast, objects with an average density greater than the fluid will sink.

Now, as an example, let us calculate the buoyant force on a $1.00 \times 10^6 \ \rm{kg}$ aluminum block wholly immersed in water.

1. First, we need to find the volume ($V_{\text{Al}}$) of the block. We can calculate this by substituting the density of aluminum ($\rho_{\text{Al}} = 2.7 \times 10^3\ \rm{kg/m^3}$) in the given formula:

2. Since the block is completely immersed in water, the volume of water displaced is the same as the volume of the block:

3. Now, we will determine the mass of water displaced by the block by substituting the density of water ($\rho_{\rm{H_2O}} = 1.0 \times 10^3\ \rm{kg/m^3}$) in the formula for density:

4. Since the buoyant force acting on the block is equal to the weight of water displaced, we can calculate the buoyancy force using Archimedes' principle as:

5. You can also use our Archimedes' principle calculator to solve the same problem with just a few clicks.

In this section, we will try to determine the density of an unknown object using our Archimedes' principle calculator. Let the true mass (mass in the air) and apparent mass (when immersed in water) of a rock be 540 g and 340 g, respectively. We will calculate the average density of this rock as follows:

1. Enter the true mass and the apparent mass of the rock as 540 g and 340 g in the respective fields.

2. Using the drop-down menu, choose fluid type as water. The density field will auto-populate. You can also enter the density of the fluid manually.

3. The Archimedes' principle calculator will display the density of the rock as 2.70 g/cm³ and the volume of the rock as 200 cm³. It will also show the buoyant force acting on the rock as 1.96 N and a message whether the rock will float or sink.

Let us consider another example, where we drop a 5 kg rock into a cylindrical container with a base surface area of 700 cm². If the height of the water inside the container changes by 2.86 cm, we can calculate the buoyant force as:

1. Select Yes under the “Do you want to calculate the volume of fluid?” option, and type the surface area of the fluid (700 cm²) and change in the height of the fluid (2.86 cm).

2. Enter the true mass of the object (5 kg).

3. The calculator will display the volume of the fluid displaced (2002 cm³) and the buoyant force (19.633 N).

Note: You can enter whatever variables you know, and the calculator will compute the rest.