Sum And Difference Identities Calculator

Welcome to Omni's sum and difference identities calculator, where we'll study the sum and difference formulas for all six trigonometric functions, e.g., the sine or cos addition formulas.

Sum and difference identities can prove extremely useful whenever a function's argument doesn't, a priori, give a simple result. In such cases, we can express the angle (and, with it, the function) as an expression with more agreeable elements. Depending on the choice, we use the sum or difference formula to end up with something easier to handle.

Although trigonometry is a broad topic with loads of generalizations, we should start where all things began: in ancient Greece.

Well, alright, this was a bit of an overstatement, but we're not too far gone. After all, we remember ancient Greeks as those who began studying mathematics in detail with formulas and proofs. In particular, geometry attracted their attention and the study of triangles. An example of where this fascination led them is the famous Pythagorean theorem. And that's where our story for today begins.

You can learn more about it in the Pythagorean theorem calculator, but for now, you only need to know that this theorem connects the sides of a right triangle with a simple formula. In other words, it tells us that the world of geometry is by no means chaotic: there are rules we need to follow. After all, we can easily see that if we take an arbitrary right triangle and increase one of its acute angles, then we need to lengthen one of the legs accordingly. Trigonometry builds on that observation.

Trigonometric functions describe the ratios between a right triangle's sides. Since these are ratios, you could theoretically find them using our ratio calculator – this might come in handy!

Below you can find a picture with formulas defining all six of them. (Note how we mention all of them in our sum and difference identities calculator.)

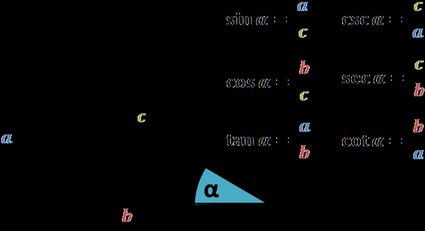
Observe how the formulas do not mention how big the triangle is. In fact, that's where a crucial property of the functions lies: even if we scale the shape to twice its size, the values of the functions will remain the same as long as we keep the angles intact.

However, we began the section by saying that trigonometry is a broad topic with many generalizations, and here, we see a significant obstacle. Indeed, by defining the functions on a right triangle, the argument, i.e., the angle, must be between 0 and 90 degrees (or 0 and π/2 in radians).

But fear not! There is a way to fix it and allow all possible angles, even negative ones. We only need to translate the whole reasoning to a two-dimensional Euclidean space, i.e., the plane.

Let A = (x,y) be a point on the plane. Define α as the angle going counterclockwise from the positive half of the horizontal axis to the line segment whose endpoints are (0,0) and A. Note how we said that α goes from one line to the other and not that it's just the angle between them. That's why we often call α a directed angle.

Clearly, we can have α larger than 90 degrees. We can even admit values larger than the full angle of 360 degrees – we simply consider the 360 degrees to be a complete lap around (0,0), and from there, we just begin the second one. And even better – we can now understand negative values too! Since we defined α to be directed, we can say that negative angles simply reverse the direction, i.e., go clockwise instead of counterclockwise.

For such arbitrary α and a point A = (x,y), we extend the definitions of all six trigonometric functions by repeating the formulas from the figure above but with a few changes: we substitute b for x, a for y, and c for √(x² + y²), i.e., the distance from (0,0) to A.

In general, calculating trigonometric functions is no easy task. Usually, we use external tools for that, so let us take this opportunity to direct you to Omni's resources that will surely make the task a piece of cake: the trigonometric functions calculator.

The sum and difference formulas allow us to calculate the value of a trigonometric function by describing it in terms of similar functions but with different arguments. In essence, we take the angle that we got initially and decompose it into a sum or difference of two other angles. We can then find the initial value by using the new ones instead and applying, correspondingly, the sum or difference formula.

As we've seen in the previous section, there are six trigonometric functions. For each, we have one angle addition formula and one angle subtraction formula. All in all, this sums up to twelve different (but similar) sum and difference identities. With that many in mind, let's start with the two most used: the sine addition formula and the cos addition formula:

sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

cos(α + β) = cos(α)cos(β) - sin(α)sin(β)

We see that both of the above angle sum formulas decompose the function of α + β (which can, a priori, be a difficult angle to work with) into an expression with α and β separately. Also, observe that the cos and sine addition formulas use both functions.

In particular, when the two angles are the same, i.e., when α = β, the cos and sine addition formulas give:

sin(α + α) = sin(α)cos(α) + cos(α)sin(α)

cos(α + α) = cos(α)cos(α) - sin(α)sin(α)

If we simplify the notation, we obtain what is often called the double angle formulas:

sin(2α) = 2sin(α)cos(α)

cos(2α) = cos²(α) - sin²(α)

where in the cosine formula, the exponent applies to the function's value, i.e., cos²(α) = (cos(α))². You can learn more about this in the double angle formula calculator.

Before we finish this section, let's apply a nifty trick to turn the above angle sum formulas into angle difference formulas. After all, we know that subtracting a number is the same as adding that number with an inverted sign. In other words, we can use the angle addition formulas to our advantage and write:

sin(α - β) = sin(α + (-β)) = sin(α)cos(-β) + cos(α)sin(-β),

cos(α - β) = cos(α + (-β)) = cos(α)cos(-β) - sin(α)sin(-β).

Next, we can use the properties of sine and cosine. In particular, we recall that sin is an odd function and that cos is an even one. This means that we have sin(-β) = -sin(β) and cos(-β) = cos(β). Therefore, the above formulas give us the sin and cos difference identities:

sin(α - β) = sin(α)cos(β) - cos(α)sin(β)

cos(α - β) = cos(α)cos(β) + sin(α)sin(β)

When we look at the sum or difference formulas, we see that the only thing changing is the sign in one of the summands. In fact, the trick we've come up with above can be applied to all angle addition formulas to give its counterparts: the angle subtraction identities.

Well, the section is called "Sine addition formula, cos addition formula," but we've also managed to sneak in two difference formulas. That means we have a third of the sum and difference trig identities behind us. We're more than ready to jump into the next section and learn about the others, aren't we?

Although the cos and sine addition formulas are the most common, the other four trigonometric functions deserve some love, too. Below, you can find all the sum and difference trig identities. For completeness, we mention the ones from the previous section as well.

• Sine:

• Cosine:

• Tangent:

• Cotangent:

• Secant:

• Cosecant:

Observe that after the two first functions, things start to get a little more complicated. The tangent and cotangent sum and difference trig identities already require some fractions. And if we look at the sum or difference formula for the secant and cosecant, we see even worse expressions with many functions multiplied together.

However, the basic idea still applies: on the right-hand side, α and β appear separately. Also, note that for whichever function, the angle addition formula varies from the difference one only by the change of signs. This property is a straightforward consequence of the same trick we used in the previous section and the parity of corresponding functions.

Phew, that seems like enough theory for today, don't you think? How about we put it to good use and solve a numeric example for a change?

Say that you're a teacher between two school years and that you must plan how to prepare the classroom for pandemic times. In other words, you must figure out how to arrange the desks so that you keep to the new standards connected with social distancing. Also, suppose you don't know our classroom spacing calculator, so you must "manually" arrange the desk.

You decide to keep to a (roughly) trapezoid shape with more students in the first row and fewer in the back. However, you seem to have forgotten your measuring tape, so you'll have to do things unconventionally.

Using your shoe and stride length, you manage to come up with approximate distances between the desks. You decide that the angle along which you align them should be 75 degrees (you've forgotten the measuring tape but not the protractor!). Also, to make it all precise, somewhere along the way, you face the problem of finding the cosine of the angle.

If there is a problem, there is also a solution, and Omni's sum and difference identities calculator seems like the right tool for the job!

The first variable in the calculator lets us choose the function we're dealing with. We need the cosine, so let's begin by choosing cosine from the list under "Function." Next, we need α and β – the two angles used in the sum and difference trig identities according to the formula shown above the variable fields.

Our angle is 75 degrees, but we have no restrictions on how to decompose it. For instance, we can observe that 75 = 30 + 45 (we say why we chose these numbers further down). We use this decomposition to apply the angle addition formula, so we input it into the sum and difference identities calculator:

α = 30, β = 45

Once we input the second value, the tool will spit out the answer. Note how the calculator gives us a step-by-step application of the formula and automatically gives the difference identity.

Still, for the scary situations where there's no Wi-Fi, let's see how to find the solution by hand.

First, let's recall that we'd like to decompose the angle as 75 = 30 + 45. To explain our choice, recall that 30 and 45 degrees appear in two very special right triangles. To be precise, the 90-60-30 triangle is, in fact, half of an equilateral triangle, and the 90-45-45 is half of a square.

That, in particular, tells us the exact relations between the triangles' side lengths. And since we defined trigonometric functions in the first section as ratios between the sides of right triangles, we can combine all that information to write:

sin(30°) = 1/2, cos(30°) = √3/2

sin(45°) = √2/2, cos(45°) = √2/2

(Note how the exact values with square roots also appear in the sum and difference identities calculator.)

Lastly, we recall the cos addition formula and apply it to our case:

cos(75°) = cos(30° + 45°)

= cos(30°)cos(45°) - sin(30°)sin(45°)

= √3/2 × √2/2 - 1/2 × √2/2

= √6/4 - √2/4

≈ 0.259.

Voilà! We have our cosine; now, the desk arrangements should go smoothly. Let's just hope that kids will always wear masks so that your effort doesn't go to waste.

To compute cos(15°) with difference identity:

1. Write 15° as the difference between two angles: 15° = 45° - 30°. We've chosen the angles for which values of trig functions are easy to compute.

2. Apply the formula cos(45° - 30°) = cos(45°)cos(30°) + sin(45°)sin(30°).

3. Plug in the values: cos(45° - 30°) = √2/2 × √3/2 - √2/2 × 1/2.

4. The final result is cos(45° - 30°) = √2(√3-1)/4.

The formula says that the cosine of the difference of two angles is equal to the sum of the product of the cosines of these angles and the product of their sines.

Trigonometry has tons of applications. For instance, you can run into trig identities in:

• Cartography;
• Engineering;
• Astronomy;
• Navigation;
• Aviation;
• Radar systems;
• Criminology;
• Medical imaging;
• Pharmacy; and...

...many others!

Not really. You'll naturally learn those that are most useful in your field of expertise. Actually, if you're familiar with Euler's formula exp(ix) = cos(x) + isin(x), you'll be able to very efficiently derive the trig identities that you need in a given problem.