Coordinate Grid Calculator
- Tessellation and tilings: types of regular grid in a two-dimensional space
- Why we can only create regular square, triangular, and hexagonal grids?
- How to calculate a coordinate grid for 2D regular tilings
- How to generate a hexagonal grid coordinates
- How to use Omni's coordinate grid calculator
- Building a triangular grid: an example
- FAQ
Welcome to the coordinate grid calculator, where you will learn how to calculate a coordinate grid with this handy tool. In this short article, we will show you:
- The basics of tiling and the regular grids in two dimensions;
- How to calculate a square and rectangular grid;
- How to calculate a triangular grid;
- The properties and math of a hexagonal grid; and
- How to use Omni's coordinate grid calculator.
What are you waiting for?
Tessellation and tilings: types of regular grid in a two-dimensional space
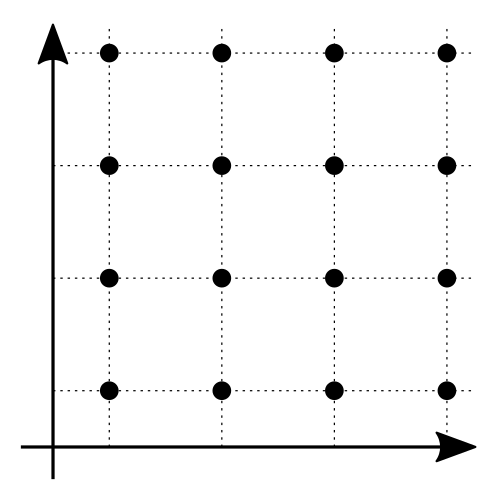
Look down at your feet: the floor you're standing on is likely covered in tiles. Tiling is a way to cover a two-dimensional surface with repeating shapes. The most common type of tiling is the square tiling, which allows you to cover a surface with a grid of equally spaced points both in the horizontal ( axis) and vertical ( axis) direction.
🙋 Are you looking for tiling in construction? We've got you covered: try our tile calculator for your flooring needs!
In the picture below, you can see an example of a square grid. If this looks familiar, it's because this is nothing but a Cartesian coordinates grid, the kind where most geometry happens!

Square tiling is the simplest example of regular tiling, which is one way to entirely cover a surface with a single type of regular shape (or "face"). In how many other ways we can perform this action? Surprisingly few! With regular shapes, we can do only:
- Square tiling;
- Triangular tiling; and
- Hexagonal tiling.
These three tiling techniques are the only ways we can cover a two-dimensional surface without leaving empty spaces. Since we use regular polygons for each of them, we can call these tilings regular. Square tiling is extremely simple, as it only involves copying and translating the same shape over and over again: we tile the plane by adding parallel lines with regular spacing, thus identifying more squares.
Triangular tiling follows the same rule, but with a twist (literally).

You can build a triangle grid by copying and pasting the same parallel lines over and over again.
Things change when we consider a hexagonal grid. You can't "propagate" this tiling by copying parallel lines, the only way is to rotate the hexagon.

🙋 Visit our hexagon calculator and hexagon quilt calculator for mathematical and crafty twists on this beautiful shape!
Why we can only create regular square, triangular, and hexagonal grids?
There is a simple mathematical reason behind this limited choice of tilings. Among the regular polygons, only squares, triangles, and hexagons have internal angles that can sum to when multiplied by an integer number. This is the condition for a tiling where cells share a vertex.
- For the square, we have .
- Considering triangles, we have .
- For the hexagonal grid, we find that .
The numbers we used in the multiplications above are also the number of cells that share a vertex in each shape's grid! Four squares meet in one corner of square tiling, six in one corner of triangular tiling, and three in one corner of hexagonal tiling.
🙋 If you need a refresh on these shapes, visit our polygon calculator: we cover all the most important properties of regular polygons and more!
How to calculate a coordinate grid for 2D regular tilings
We can't define generic rules to calculate a coordinate grid. Some tilings are straightforward, others slightly more complex. To fill a hexagonal grid, you need multiple formulas and conditions, making hand-calculation of the coordinates a tedious task.
In this section, we will try to lay down the rules to create a grid.
Creating a square or rectangular coordinate grid
To calculate a coordinate grid's points in the case of a rectangular or square grid, you simply have to propagate the dimensions of the cell in the proper direction. For a square grid with a cell side equal to , we can create a grid originating from the point by following these simple rules:
where:
- — The index of the point we are considering; and
- and — The offsets in the two directions.
A few words about the offsets: the most likely to occur in a square grid places the origin of the grid in the center of the starting cell. In this case, the offsets would be:
- ; and
- .
To generate the points of a rectangular grid, the calculations for the coordinate grid change only slightly. Defining the dimensions of the rectangular cell as and (for the and direction respectively), we use the following formulas:
Generating a triangular grid
To generate a triangular grid from a starting point , start by creating a row of points. If your cell has side , then you can find your points with the formula:
To create other rows of points, we need to move vertically by the height of the triangular cell:
Each row then has a vertical coordinate given by:
That's not all: every second row is shifted by .
To move the origin of a triangular grid to the center of the cell, we need to use the following offsets:
- ; and
- .
How to generate a hexagonal grid coordinates
Generating a hexagonal grid's coordinates is not easy. First, there are multiple "neat" offsets, even apart from the center (thanks to the many corners in a hexagon). Moreover, we find an increased number of possible distances between the points. We will leave the math to our calculator: in this section, we will only introduce the possible types of hexagonal grids and the spacing you can find there.
For the coordinates of a hexagonal grid where the cell has a horizontal side, we can use this reference image to identify the characteristic spacing of this grid.
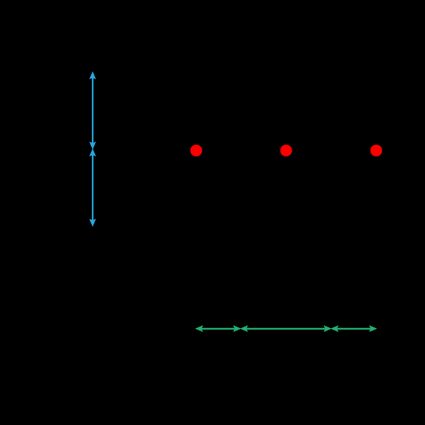
We marked in red the possible origins of the hexagonal grid coordinates, which coincide with a vertex or to the center of the cell.
We can introduce the vertical cell, too: the spacing is the same, only tilted, but we can now identify different origin points.
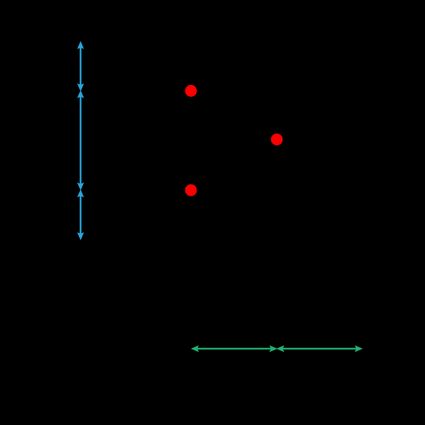
How to use Omni's coordinate grid calculator
Omni's coordinate grid calculator saves you a lot of time by doing tedious calculations for you. To use our grid calculator, simply choose the type of tiling you need. We give you five options!
- Square grid;
- Rectangular grid;
- Triangular grid; and
- Hexagonal grid (both horizontal and vertical).
Then, you need to insert some other parameters:
- The number of points per side of the grid; and
- The necessary cell parameters (one or two sides).
We give you the possibility of visualizing the first 100 points; then, you will only be prompted to download the file.
Building a triangular grid: an example
Let's check the step needed to build the first 25 points of a triangular grid. Follow these steps:
- Choose the placement of the origin. We will set it at .
- Choose the length of the triangle cell's side: we went for a neat .
- Next up: generate the first two rows of points:
- The first one has and with .
- The second one has and with .
- To generate the following rows, add to the value of in the two cases we've seen in the last point.
FAQ
What are the three possible regular tilings?
There are only three possible regular tilings (tilings that use only translation and rotations of regular polygons):
- Square tiling;
- Triangular tiling; and
- Hexagonal tiling.
All other regular polygons leave gaps in the plane when you attempt to cover it using such shapes.
How do I calculate the coordinates in a triangular grid?
To calculate the grid coordinates using a triangular cell, follow these simple rules:
- Generate the first row of points: they share the same
ycoordinate and are spaced by the side of the cellℓ. - Generate new rows by adding integer multiples of
ℓ × √3/2(the cell's height). - Shift every second horizontally by
ℓ/2. - Translate the grid by the desired offset by subtracting the vertical and horizontal offset from each coordinate.
Why is a hexagonal grid special?
Hexagonal grids are unique for an interesting series of reasons:
- Hexagons don't tile the plane by simple repetition of parallel lines (as squares and triangles).
- Hexagons tile a plane using the smallest perimeter per number of cells: it means that every interface between cells is reduced.
- The triangles in a triangular grid are a simple subdivision of a hexagonal grid.
It comes as no surprise that nature is filled with hexagons: from beehives to planets, from foam to cells: the hexagon minimizes the energy required for things to stay close to each other.
What are the coordinates of a square grid with side 1.5?
To generate the coordinates of a grid of squares with side ℓ = 1.5, follow these easy steps:
- Choose the grid's origin: we place a vertex in the point
(0,0). - Choose the number of points in each direction: try with a 4×4 grid.
- Start by generating the first row. Fix
y=0and create the points with the formulax = ℓ × i = 1.5 × i, withigoing from0to3. You'll get(0,0),(1.5,0),(3,0),(4.5,0). - Generate each new row by adding
ℓto theycoordinate.