Present Value of Annuity Calculator

The present value of annuity calculator is a handy tool that helps you to find the value of a series of equal future cash flows over a given time. In other words, with this annuity calculator, you can compute the present value of a series of periodic payments to be received at some point in the future.

If you read on, you can learn what the annuity definition is, what is the present value of annuity as well as how to use this annuity payment calculator. Besides, you can find the annuity formulas and get some insight into their mathematical background.

If you're unfamiliar with the time value of money concept, you might want to dive deeper into our time value of money calculator!

A wide range of financial products all involve a series of payments that are equal and are made at fixed intervals. If you have ever met such a scenario, you have met an annuity. The two conditions that need to be met are constant payments and a fixed number of periods. For example, $500 to be paid at the end of each of the next five years is a 5-year annuity.

If you would like to evaluate an annuity, there are two aspects to be considered: the present and future value of the annuity. While we designed this calculator to determine the present value of annuities, we have also built a tool to help you calculate the future value of annuities; please find it here at our future value of annuity calculator.

There are several ways to categorize annuities. You may hear about a life annuity, where payments are made for the remaining lifetime of the annuitant (the person who receives the annuity payments). Since this kind of annuity is paid only under a specific condition (i.e., the annuitant is still alive), it is known as a contingent annuity. If the contract defines the period in advance, we call it a certain or guaranteed annuity.

Annuities are further differentiated depending on the variability of their cash flows. There are fixed annuities, where the payments are equal, but also variable annuities, that you allow to accumulate and then invest based on several, tax-deferred options. You may also find equity-indexed annuities, where payments are adjusted by an index.

We can differentiate annuities even further based on whether they are deferred or immediate annuities. Immediate annuities are specific financial constructions offered mostly by insurance companies where, following a lump sum payment, the annuitant starts to receive a monthly payment for the rest of his/her lifetime (or for a set of periods, such as 10 or 20 years). This type of annuity operates as a pension plan and is designed for people who are already retired and are looking for a guaranteed retirement income.

Deferred annuities usually earn interest and grow in value, so that to delay the payment by several years increases the payout of the monthly payments. People yet to retire or those that don't need the money immediately may consider a deferred annuity.

An essential aspect of distinction in this present value of annuity calculator is the timing of payments.

In this context, there are two types of annuities to define:

• Ordinary annuity or deferred annuity: payments are made at the ends of the periods – mortgages, car loans, and student loans are conventionally ordinary annuities.

• Annuity due: Payments are made at the beginning of each period – rental lease payments, life insurance premiums, and lottery payoffs (if you are fortunate enough to win one!)

The easiest way to understand the difference between these types of annuities is to study a simple case. Let's presume that you will receive $100 annually for three years, and the interest rate is 5 percent; thus, you have a $100, 3-year, 5% annuity.

Payment Amount = 100 dollars

Interest Rate = 5%

Annuity Term = 3 years

Below this text, you will find a graph that shows the timelines of the two types of annuity with their present values. As you can see, in the case of an annuity due, each payment occurs a year before the payment at the ordinary annuity. The advanced cash flow has a direct impact on the present value of the annuity: a dollar today is worth more than a dollar tomorrow. Therefore with the annuity due, the present value of the annuity is higher than with the ordinary annuity.

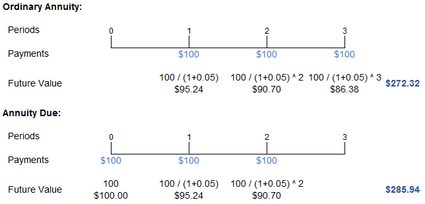
You can also learn the basic logic behind the present value of an annuity: it is merely the sum of the discounted cash flows estimated over each period. How to find these single payments? Take a look at the ordinary annuity in the image above. The first payment is discounted by one period's interest, the second by two periods, and the third by three. If you want to read more about the concept of discounting, you may check our discounted cash flow calculator, where you can find more details. Or, if you would like to calculate the rate, you can apply our discount rate calculator.

Although this approach may seem straightforward, the calculation may become burdensome if the annuity involves an extended interval. Besides, there may be other factors to be considered that further obscure the computation. If you read on, you can study how to employ our present value annuity calculator to such complicated problems.

In the previous section, we discussed how a simple annuity operates. However, you can still use our present value of annuity calculator to solve more complex financial issues. In this section, you can familiarize yourself with this calculator's usage and its mathematical background.

As a starting point, let's have a brief overview of the specific terms you can find in our calculator.

• Payment amount (PMT) is the amount paid in or out (cash flow) for each period.

• Interest rate (r) is the annual nominal interest rate expressed as a percentage.

• Annuity term constitutes the lifespan of the annuity.

• Compounding frequency (m) refers to the number of times the interest is compounded. For example, when compounding is applied annually, m = 1; quarterly, m = 4; monthly, m = 12, etc. You can choose the frequency as continuous as well, which is an extreme form and the theoretical limit of compounding frequency. In such a case, m = infinity.

• Payment frequency (q) indicates how often the payments will materialize.

• Type of annuity (T) signifies the timing of the payment in each payment period (ordinary annuity: end of each payment period; annuity due: the beginning of each payment period).

• Present value of the annuity (PVA) is the present value of any future cash flows (payments).

In the section labeled growth rate and additional information, you can reach the following specifications:

• Growth rate of the annuity (g) is the percentage increase of the annuity in the case of a growing annuity.

• Number of periods (t) shows the annuity term in years.

• Equivalent interest rate and Periodic equivalent interest rate are the interest rates computed when the payments and compoundings occur with a different frequency (cannot be set manually).

Now as that you know all the financial terms appearing in this calculator, let's do a quick example of how the annuity formulas can be applied.

The two basic annuity equations are the following:

• Ordinary Annuity:

  PVA = PMT × ((1 / i) - (1 / (i × (1 + i)ⁿ)))

• Annuity Due:

  PVA = PMT × ((1 / i) - (1 / (i × (1 + i) ⁿ))) × (1 + i)

  n = m × t, where n is the total number of compounding intervals

  i = r / m, where i is the periodic interest rate (rate over the compounding intervals)

Just to clarify, in the following annuity formulas, we refer to the ordinary annuity.

• Present Value of a Growing Annuity (g ≠ i):

  PVA = PMT / (i - g) × (1 - ((1 + g) / (1 + i))ⁿ)

• Present Value of a Growing Annuity (g = i):

  PVA = PMT × n / (1 + i)

• Present Value of an Annuity with Continuous Compounding (m → ∞)

  PVA = PMT / (e^r - 1) × (1 - 1 /e^rt)

  where e stands for the exponential constant, which is approximately 2.718.