Recessed Lighting Calculator

This recessed lighting calculator will help you find each recessed lighting fixture's placement and spacing when planning a rectangular ceiling's lighting layout.

Correctly placing a lighting fixture on a ceiling will help you optimally utilize its potential lighting capacity. We don't want to place our recessed lighting fixture very close to the wall, and we don't want them to be too close to each other as well and flood an area of the room.

In this recessed lighting layout calculator, we'll discuss the following:

• What recessed lighting is;
• How to use this recessed lighting calculator;
• How to calculate recessed lighting spacing and placement; and
• Some frequently asked questions about recessed lighting installation.

Keep reading to start learning.

Recessed lighting is a lighting fixture with a light source inside a surface like a ceiling. An incandescent bulb installed openly on a light socket is not recessed lighting unless we cover its sides with, let's say, a can, a tube, or a box so that the illumination will seem like it's coming from inside the box (and not radially in almost all directions from a bulb).

Now that we know what recessed lighting is, let us now explore the recessed lighting calculator.

To use our recessed lighting layout calculator:

1. Enter the length and width of the ceiling where you'll install your recessed lighting.

2. Choose the number of columns of recessed lighting along the width of your ceiling.

3. Select the number of rows of recessed lighting along the length of your ceiling.

4. Decide whether you want recessed lightings that are positioned at the centers of the recessed lighting grids. Answer Yes to the "Include center-positioned lightings?" question in our tool if you want them, and No if you don't want them.

Our calculator will then display the corresponding measurements for the offset and spacings of the lighting fixture, depending on your selection.

If you need to know how much illumination is required for any room type, we have our lighting calculator that you can use for that.

Calculating the distances of the recessed lighting fixtures from each other and from the edge of the ceiling follows a simple concept. Let's say we want 2 columns of recessed lighting along the width of the room and 3 rows of recessed lighting along the length of the room, for a total of six lighting fixtures. For that, all we have to do is equally divide the room into six smaller rectangles by equally dividing the room width by two and by dividing the room length equally by three, as shown in the illustration below:

We then place our recessed lighting fixtures at the centers of these six boxes. We can calculate the distance of the upper leftmost fixture from the upper edge of the ceiling or the outer row offset using this formula:

where:

• $a_\text{o}$ — Outer row offset;
• $A$ — Surface length; and
• $r$ — Number of rows of lighting fixtures.

The outer row offset is also the distance of the lowermost fixtures from the lower edge of the ceiling.

Next, we can calculate the vertical row spacing, $a_\text{i}$, of the recessed lighting fixtures using this equation:

You can refer to the illustration below to clearly imagine what the variables $a_\text{o}$ and $a_\text{i}$ are:

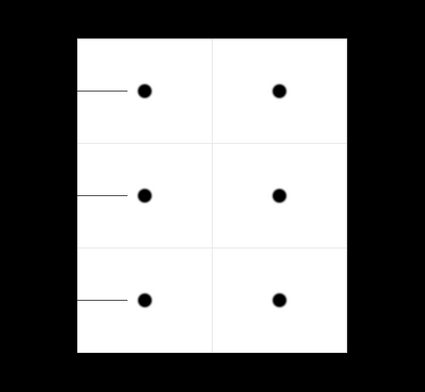
On the other hand, we can calculate the outer column offset, or the distance of the outer fixtures from the sides of the ceiling, using this equation:

where:

• $b_\text{o}$ — Outer column offset;
• $B$ — Room width; and
• $c$ — Number of columns of lighting fixtures.

Then for the column spacing, $b_\text{i}$, we use this formula:

In the illustration below, you can see which ones are $b_\text{o}$ and $b_\text{i}$:

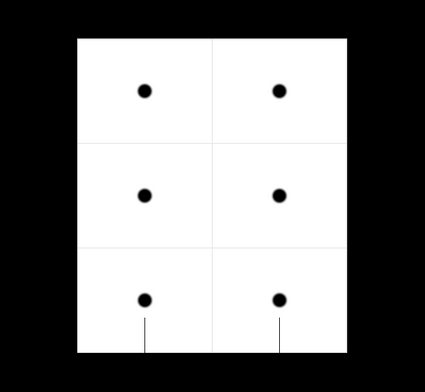
If we want to install lighting fixtures like chandeliers or additional recessed lighting, we can consider the intersection of the boxes we form by dividing the room ceiling into columns and rows.

For the centered lighting's vertical offset, $y_\text{o}$, from the upper or lower edge of the ceiling, we calculate that as sown below:

If there is more than one centered lighting, we can determine their spacing using this equation:

where:

• $y_\text{i}$ — Centered lighting's spacing.

On the other hand, we can calculate the distance of our centered lighting's distance from the left or right side of our ceiling using this equation:

where:

• $x_\text{o}$ — Centered lighting's horizontal offset.

Likewise, if there are two or more centered lighting along the horizontal, we can calculate their spacing as follows:

where:

• $x_\text{i}$ — Centered lighting's spacing.

Recessed lights should not be very close or too far from each other. They should be adequately spaced on a surface to light a room evenly.

Let's say we want to install two recessed lights on a ceiling. We can divide the ceiling into two equal segments, then position each recessed light at the center of each ceiling segment.

To layout recessed light fixtures, say with four recessed lighting fixtures on a square ceiling, 3 meters wide:

1. First, divide the ceiling into how many recessed lighting fixtures you want to install. Since we want four recessed lightings, we need to divide the ceiling into four equal squares on a 2-by-2 layout. If our room has a long rectangular ceiling, we might want to have a single column of four recessed lights.

2. Having decided to have a 2-by-2 grid ceiling layout, we then divide the ceiling into 4 squares with 1.5 meters by 1.5 meters dimensions.

3. Finally, we place the recessed lighting fixtures at the center of each square, where their locations would be 1.5 meters / 2 = 0.75 meters away from the walls.

The optimal spacing of recessed lighting fixtures is the distance between themselves, wherein all the recessed lighting fixtures will have precisely equal areas to illuminate. That is, if you only have to install one recessed lighting, its position should be at the center of the ceiling. Installing 2 recessed lightings requires us to split the ceiling in half so that each fixture will illuminate the corresponding floor areas beneath them almost equally.

To calculate recessed lighting spacing, we need to:

1. Determine the dimensions of the ceiling; say its length is 5 meters and width is 3 meters.

2. Let's say we want to install four recessed lighting fixtures arranged in two columns and two rows such that the recessed lightings form a rectangle.

3. Divide the ceiling width into two to find the spacing of the fixtures along this direction. In this case, we have:

   spacing = 3.0 m / 2 = 1.5 m

4. We divide this spacing by 2 to find their offset from the edge of the ceiling to have:

   offset = 1.5 m / 2 = 0.75 m

5. Repeat steps 3 and 4 for the other ceiling dimension to get the other spacings equal to 5.0 m / 2 = 2.5 m and 2.5 m / 2 = 1.25 m.