Plant Spacing Calculator

Even though growing your food doesn't have to be seasonal, spring comes with blooms, blue skies, and warm weather 🌤 that inspires many people to experiment with gardening. You can never go wrong using your backyard, balcony, patio space, or containers to grow herbs and fresh vegetables 🍅🥕🥒🥜; aside from the benefit of accessing nutritious and healthy food, you'll be improving the environment, exercising in nature, and learning new skills!

But gardening or landscaping can be daunting to plan, which is why we created the Plant Spacing Calculator to help you in the critical planning stage to navigate how to calculate plant spacing. You can figure out the proper spacing for any plant, hedgerow, and land area with the plant spacing calculator – regardless of whether you want a square grid ⏹, a rectangular grid, or triangular spacing 🔼. If you are planning on planting bulbs, you might want to check out our dedicated bulb spacing calculator. Depending on the kind of crop you want to grow, you can also measure the yield that you'd get!

If you are on a budget, you can also estimate the total cost of purchasing the plants before you begin 💲. To determine the amount of mulch you'll need for your garden, use the mulch calculator. And make sure to check out the fertilizer calculator too.

Most newbies begin their gardening career in the springs because of the favorable weather condition. There is no better time to start your planting in readiness for the August harvests. But seasoned gardeners know how to extend their harvests by efficiently planting new crops that’ll be available for harvests in the off-season. It’s a method called succession planting.

With suitable crops, you can also increase the availability of crops in your garden all year round. A simple way to do that is by quickly planting crops suited for the early periods of a successive season, late in the preceding season. Some plants you should consider having on your gardens for an all-green season are:

• Spring 🌤 – Parsley, Cilantro, Parsnips, Rhubarb, Collards, Radishes;

• Summer ☀ – Tomatoes, Peppers, Cucumbers, Eggplant, Okra, Watermelons;

• Fall 🌦 – Lettuce, Carrots, Red beets, Broccoli, Cabbage, Chicory, Snap beans;

• Winter ❄ – Arugula, Kale, Spinach, Carrots, Turnips, Winter squash, Asparagus, Leeks, Onions.

Gladly, these plants have similar plant spacing requirements that allow you to grow them successively without significant changes to your garden grid.

A square grid of plants is pretty simple to understand: you divide the area into squares of equal side length and put one plant in each corner.

For a rectangular grid (i.e., row planting), you divide the area into rows and spread plants evenly along each row. Planting in rows means you can have more space between rows and less space between plants within the row. It makes walking between rows easier and has potential benefits for disease management, but it isn't as space-efficient as triangular spacing.

If you want triangular spacing, you need to create a lattice of equilateral triangles (they all have sides of the same length, and all internal angles are equal to 60 degrees), and place a plant in each corner. This arrangement maximizes the use of space but can have the consequence of diseases spreading more easily in mono-crop farming. Triangular spacing is frequently used in landscaping.

Hedgerows (or hedges – if you're planting a single plant species or mono-cropping) are "closely spaced shrubs and sometimes trees" grown and maintained as boundaries, barriers, fences, or windbreaks. Garden hedgerows are often evergreen species, and they can also produce food, e.g., Cumquats, Pomegranates, and Lemon myrtle. If you grow an edible hedge for privacy and food, it's called a Fedge 😏. Hedgerows are essential parts of landscaping projects.

The ideal spacing for most hedge plants is 33cm (3 plants per meter). The exceptions are low hedge plants and those that take longer to mature, e.g., Dwarf box (around 15cm apart) and Common box (around 20cm apart). Otherwise, depending on how dense you want your hedges or how soon you want them to 'fill in' the spaces between them, you may decide to grow them closer. Or plant multiple rows (double, triple, etc.) to improve the compactness. You plant multiple single rows parallel in such cases, using the triangular plant grid with 40cm between rows.

Generally, maintaining an equidistant between your plants reduces the risk of competition for water and nutrients between them. But keep in mind that recommendation may vary based on plant species, planting costs, and your hedgerows' function.

You can figure out the plant spacing for your gardens and hedgerows using this plant spacing calculator.

First, select the type of planting you wish to plan: a garden or a hedgerow.

Let's start with the "Garden grid" option:

1. Select the type of grid: square, rectangular, or triangular.

2. Determine the width and length of the area you want to cover with plants. We will assume an orchard with a width of 240 m and a length of 320 m.

3. Determine the width of the border where you won't be putting plants. For our orchard, we will assume the border is 2 m.

4. Decide on the spacing, i.e., the space between the centers of the plants. Let's take 3.5 m for our example.

   • You can find the right spacing information on the seed packets or ask in your local plant nurseries or home garden center; or

   • You can estimate based on the target plant size and depending on the type of plant. If you want a 1 m wide spacing, you will plant at least 1 plant / m², unless you want the plants to overlap or grow faster.

5. The calculator will tell you how many plants you need. Notice that if you chose rectangular or triangular spacing, the plant spacing calculator will also tell you how much space you need to leave between the rows.

   Let's say we go for triangular spacing. We will be able to plant 7,059 plants, and the rows need to be spaced 3.03 m apart so that there is exactly 3.5 m between each plant in all directions.

   In triangular spacing, even rows will sometimes have one less plant, as shown in the image within the calculator. Don't worry. The plant spacing calculator will take this into account.

6. Use the Plants cost section of the calculator to estimate the cost of purchasing the plants you need for your planting project, given the total plants. Just input the total plants and cost-per-plant to get the total cost.

And here is how to proceed with hedgerows:

Select the Number of rows and choose if you want to find how many plants you need for a certain spacing requirement or the appropriate spacing for how you should arrange your plants, then:

• Input the Length of hedge and Plant spacing to get the total Number of plants you need for your hedge's length; or
• Input the Total plants and Plants per row to get the total Plant spacing you need for your hedge's length.

Sometimes you may have a target plant density or plant population for a particular species (such as 2 plants per m²), and you need to find out how to calculate the plant spacing between each plant. The formula to find plant spacing from plant density is different depending on the type of grid.

For a square grid, the formula is:

plant spacing = √(1 / density)

and for a triangular grid, the formula is:

plant spacing = √(2 / (√3 × density))

where density could be plants/m² or plants/ft² and plant spacing could be m or ft, accordingly.

Did you know that you might fit a different number of plants in the same area depending on which way you orient the triangular grid? Sounds bizarre, right?

You can try switching around your numbers for width and length to see how it changes the total number of plants. It makes a lot more sense when you can visualize the triangular grid in the diagram below:

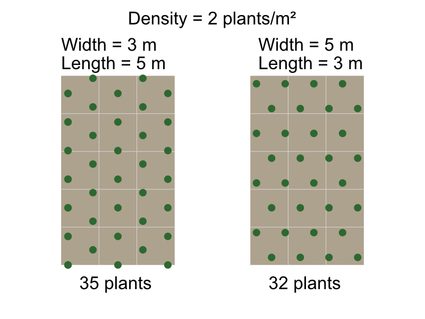
As you can see, turning the triangular grid by 90 degrees changes the grid layout. It can therefore result in a different number of plants since a triangular grid is not bi-symmetrical. If aesthetics are an integral part of your planning, try playing around with different grid orientations for different effects!