Young-Laplace Equation Calculator
Our Young-Laplace equation calculator will help you solve the Young-Laplace equation for a liquid in a column and determine its capillary pressure and height. You will never have difficulty solving the Laplace equation again!
Capillary pressure can act as a driving force to transport liquid in a thin tube without the help of (or even against) any external forces like gravity. In the article below, we shall learn how to calculate capillary pressure using the Young-Laplace equation, among other things.
Surface tension and contact angle
Before learning how to calculate the Young-Laplace equation, let us discuss two relevant liquid interfacial properties — surface tension and contact angle. We will discuss water here for simplicity, but the following discussion is valid for all liquids.
Surface tension
Take a test tube half-filled with water. The water molecules in the bulk of the water experience cohesive forces through hydrogen bonding with other water molecules uniformly on all sides.
On the other hand, the water molecules at the water-glass or water-air interface are exposed to different forces. Since there will be more water molecules below the surface than above it, the water molecules at the surface will develop a net attraction into the bulk of the water through cohesive hydrogen bonding.
As a result, the water-air interface develops a membrane-like surface that tends to contract to a minimum surface area and reduce surface energy. We call this property the surface tension of a liquid. You can learn to calculate it using our surface tension calculator.
Contact angle
When we place a liquid drop on a solid surface, the angle the liquid-gas interface makes with the solid-liquid interface is known as the equilibrium contact angle.
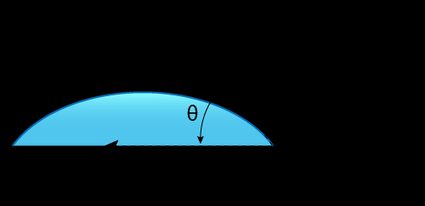
The contact angle is unique to the given solid, liquid, and vapor at a given temperature and pressure. It quantifies the wettability of a solid surface by the given liquid. A smaller contact angle means that the solid is 'wettable' by the liquid, and the liquid is more strongly attracted to the solid surface (adhesion) than other liquid molecules (cohesion).
Conversely, a larger contact angle means that the cohesion of liquid molecules is stronger than the adhesion with the solid surface, and we can say that the solid and liquid repel each other.
What is capillary pressure?
Capillary pressure is the pressure between two immiscible fluids in a narrow space (like a thin tube). In other words, it is the pressure difference across the interface between two immiscible fluids. This pressure develops from the interactions between the two fluids and the solid walls of the tube itself. The interfacial properties we discussed so far come into play.
The capillary pressure is given by:
where:
-
— Capilarry pressure;
-
— Pressure of the non-wetting phase; and
-
— Pressure of the wetting phase.
Which fluid acts as the wetting phase and which serves as the non-wetting phase depends on the fluids' surface tension and contact angle. A fluid with a contact angle less than is usually the wetting fluid, while a fluid with a contact angle greater than is the non-wetting fluid.
It also depends on the system in question. In an oil-water system, water is typically the wetting fluid, while oil is typically the wetting fluid in a gas-oil system.
Young-Laplace equation for capillary pressure
The Young-Laplace equation relates the capillary pressure between two static immiscible fluids to the surface tension at the interface.
If the two fluids are in a thin tube, their interface will form a meniscus — a curved surface.
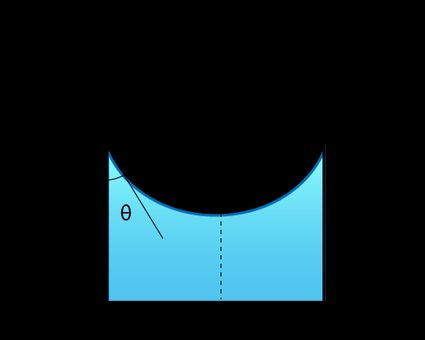
In this case, the Young-Laplace equation gives the capillary pressure formula:
where:
-
— Laplace pressure, the pressure difference across the interface between the two fluids;
-
— Surface tension at the interface; and
-
— Radius of curvature of the interface.
🙋 In the pressure difference formula above, the Laplace pressure is defined as , where the interface between fluid and curves into fluid . In the case of water in a thin tube, since the interface curves into the water, the Laplace pressure would be .
From the figure above, we observe the relation:
where:
-
— Radius of the tube; and
-
— Contact angle.
Using this relation in (2), the Young-Laplace equation will become:
For a case where the fluid is in a space more complex than a tube, say in soil pores, the Young-Laplace equation given in (2) is generalized to:
where and are the two principal radii of curvature.
Solving the Laplace equation for height of the fluid in a thin tube
When we vertically place a thin tube in a liquid container, the liquid rises to fill some portion of the tube. At a particular height, the capillary pressure and the hydrostatic pressure of the liquid in the column will reach an equilibrium.
Using the capillary pressure formula (4), we get:
where:
-
— Density of the liquid;
-
— Gravitational acceleration;
-
— Height of the liquid in the thin tube at equilibrium.
🔎 For more on hydrostatic pressure, head to our hydrostatic pressure calculator.
Calculating capillary pressure using this Young-Laplace equation calculator
Our Laplace equation solver is straightforward to use:
-
Select the fluid rising in the tube. This will auto-fill values for the fluid's surface tension and density. Alternatively, you can enter custom values in these fields.
-
Provide the inner radius of the tube and the contact angle. Alternatively, enter the radius of the meniscus if this value is known.
-
The Laplace equation solver will instantly calculate the capillary pressure/pressure difference across the interface. You can also calculate the pressure inside or outside by providing one of these values.
-
Using the density of the fluid and the gravitational acceleration value, the Young-Laplace equation calculator will also tell you the height of the fluid column!
Love our Young-Laplace equation calculator? If you're interested in other kinds of fluid pressure calculations, we recommend our osmotic pressure calculator and partial pressure calculator.
FAQs
What is the capillary pressure of water in a 2 mm diameter tube?
Assuming a contact angle of 20° and surface tension of γ = 0.07294 J/m² at sea level, the capillary pressure of water in a 2 mm diameter tube is 137.08 Pa. To calculate this value, follow these steps:
-
Divide the radius of the tube by the cosine of the contact angle to get the meniscus radius:
R = a/cos(θ) = 1 mm/ cos(20°) = 1.0642 mm
-
Divide the surface tension by the meniscus radius and multiply the quotient by 2 to get the capillary pressure:
pc = 2⋅γ/R = (2 × 0.07294 J/m²)/1.0642 mm = 137.08 Pa
How do I calculate the Laplace equation without the meniscus radius?
The radius of the meniscus is equal to the radius of the tube divided by the cosine of the contact angle. Hence, you can calculate the Laplace equation using the formula Δp = 2⋅γ⋅cos(θ)/a, where a is the radius of the tube and θ is the contact angle.
Why is capillary pressure important in the petrochemical industry?
Capillary pressure studies of sub-surface hydrocarbon reservoirs can reveal crucial reservoir conditions and properties, such as fluid saturation, cap-rock seal capacity, relative permeability, and phase behavior of reservoir fluids. This information can influence engineering decisions about extraction methods and recovery.
What causes capillary pressure?
Capillary pressure develops due to the interactions between two immiscible fluids at the interface and the solid walls of the container. Interfacial tension is a primary driver of this phenomenon.