Michaelis-Menten Equation Calculator

New

The Michaelis-Menten equation calculator allows you to discover the kinetics of one-substrate reaction catalyzed with an enzyme. Michaelis-Menten kinetics allows you to calculate the rate of the reaction, V, substrate concentration, K_m, and the maximum rate of reaction, V_max.

In the article below, we will equip you with essential knowledge regarding Michaelis-Menten enzyme kinetics, and all the details of the M-M formula. Read on!

How to use the Michaelis-Menten equation calculator?

To obtain the desired rate of the reaction, $\rm V$ , you will need the following data:

$\rm V_{\rm max}$ of the reaction – maximum rate of the reaction;
$\rm [S]$ – molar concentration of the substrate; and
$\rm K_{\rm m}$ – the Michaelis constant (see the section below).

\text V = \frac{\text V_\text{max} \times [\text S]}{[\text S] + \text K_\text m}

Both $\rm V$ and $\rm V_{\rm max}$ in biochemistry are written in units of s¯¹ (1/s). If you entered the concentration in molars (M), the $\rm V$ unit would be equal to M/s. If your concentration is given in micromolar (μM), the $\rm V$ unit will look as follows: μM/s.

If you wish to follow the change in concentration of your substance, visit the solution dilution calculator.

Remember, you may also transform the formula so that it'll fit your needs better. To give you an example, here's the $\rm V_{\rm max}$ equation:

\text V_ \text {max} = \frac{\text V (\text K_\text m + [\text S])}{[\text S]}

Try our molarity calculator to understand more about molar concentrations.

Michaelis Menten equation derivation and use

The Michaelis-Menten Model is based on a kinetic concept, expressed in the following enzyme equation:

E + S ⇄ ES → E + P

where:

E stands for Enzyme;
S stands for Substrate; and
P stands for Product.

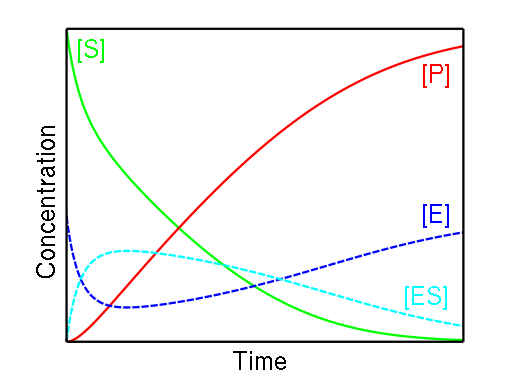
The enzyme binds with the substrate, and that connection results in a product forming. The enzyme can bind and unbind with many different substrates back and forth multiple times, which is why this reaction happens both ways. This notation is, in fact, three enzyme kinetics equations in one.

E + S → ES, speed of the reaction: $\rm k_1$ ;
ES → E + S, speed of the reaction: $\rm k_2$ ; and
ES → E + P, speed of the reaction: $\rm k_3$ .

(Check out our activation energy calculator for determining the activation energy of any chemical reaction).

The amount of ES remains relatively stable during the course of a reaction until the amount of substrate is close to 0. Two essential observations led to the creation of the formula used in our Michaelis-Menten equation calculator:

When the concentration of the substrate is low, the speed of the equation is directly proportional to the substrate; and
When the level of substrate is high, the speed becomes independent and does not exceed the maximum rate.

Michaelis and Menten had to define a new constant that describes the stability of the ES complex; this new constant had to have the same unit as the substrate.

How to calculate the Michaelis constant?

If you're looking for the $\rm K_m$ equation, you're in the right place.

As we've already mentioned, the Michaelis constant is equal to the amount of substrate present when the reaction rate is at half of the maximum. You need to carefully draw a graph depicting all the circumstances of your reaction. The X-axis must be the reaction rate, while the Y-axis should match the concentration of the substrate.
Another way to calculate $\rm K_m$ in an enzyme reaction is to try the formula that uses the speed of reactions enumerated in the paragraph above: $\rm k_1$ , $\rm k_2$ , $\rm k_3$ .

\qquad \text K_\text m = \frac{\text k_2 + \text k_3}{\text k_1}

Finally, we may transform the Michaelis-Menten equation so that the result will be our K_m:

\qquad \text K_\text m = \frac{\text V_\text {max}[\text S] - \text {V[S]}}{\text V}

Molar Mass Calculator