Rate of Effusion Calculator

This rate of effusion calculator finds the rate of diffusion/effusion of different gasses based on their molar mass.

Are you doing research for a project asking you what Graham's law of diffusion of gases is? Or maybe you already know what Graham's law is, and now you want to study the industrial applications of Graham's law of diffusion or effusion? Our rate of effusion calculator will surely help you in both cases!

Diffusion, in general, refers to the process in which the particles of a substance move from an area of higher concentration to an area of lower concentration. The diffusion of gases refers to the process in which the molecules of one gas distribute themselves into another gas.

Graham's law of diffusion definition for gases states that:

The rate of diffusion or effusion of a gas is inversely proportional to the square root of its molecular weight.

You can write the formula for Graham's law of diffusion or effusion of gases as:

$\text {rate }_1 / \text{rate }_2 = \sqrt{ \text{mass }_2 / \text{mass }_1}$

where:

• $\text {rate }_1$ and $\text{rate }_2$ - Rates of effusion or diffusion of gas 1 and 2, respectively, measured moles per unit time.
• $\text{mass }_2$ and $\text{mass }_1$ - Molar masses of gas 1 and 2, respectively.

You may want to try out our rate of effusion calculator to practice how the rates or masses are calculated.

You may also want to try out our molar mass of gas calculator to understand the significance of the molar mass of gases in various situations.

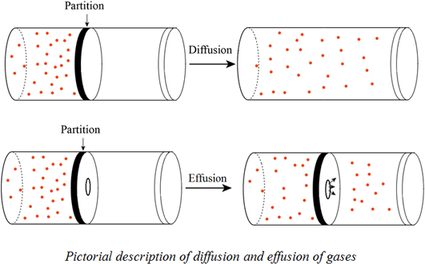
The picture above is a depiction of diffusion and effusion. The gas molecules have a different way of spreading based on the conditions.

When the partition between gases is removed, the particles move freely and spread as far away as they can; this is diffusion.

In the second part of the picture, the process of effusion occurs because the molecules escape from a small opening created in the partition.

In our daily lives, we experience the process of diffusion frequently: when you spritz the perfume on yourself and receive a compliment on the fragrance from the other side of the room. The fragrance travels by diffusing through the air.

The thermal diffusivity calculator will explain the diffusion process, which is how molecules travel in different mediums.

The derivation of Graham's law of diffusion is based on the kinetic theory of gases, which is also a base for the theoretical explanation of the law.

How does the rate of effusion calculator work? Let's start by deriving the formula for Graham's law of diffusion and effusion of gasses using the standard kinetic energy equation:

$1/2 (\text m_1 \times \text v_1^2) = 1/2 (\text m_2 \times \text v_2^2)$

Multiplying both sides by 2:

$\text m_1 \times \text v_1^2 = \text m_2 \times \text v_2^2$

Rearranging the equation:

$\text v_1^2 / \text v_2^2 = \text m_2 / \text m_1$

After taking the square root of both sides, the equation summarizes as:

$\text v_1 / \text v_2 = \sqrt {\text m_2 / \text m_1}$

Now replace mass $\text m$ with molar mass $\text M$.

$\text v_1 / \text v_2 = \sqrt {\text M_2 / \text M_1}$

where:

• $\text v_1$ and $\text v_2$ - Rates of diffusion or effusion; and
• $\text M_1$ and $\text M_2$ - Molar masses of gases.

Our rate of effusion calculator is based on this formula and can be used to calculate either rate of diffusion/effusion or molar masses of gases, whichever suits your need.

Effusion is when the molecules of a gas escape from a container with tiny openings. You might have noticed that a helium balloon🎈 eventually deflates no matter how hard you tie its end. This is because balloons are made of rubber, a porous material, so there are openings through which gases can escape.

Graham's law of effusion is another name for Graham's law of diffusion of gasses.

The discovery of Graham's law of diffusion has led to it being used in various practical and industrial applications, some of which are given below:

• Graham's law of diffusion of gases helps in the separation of gases that have different densities.
• It helps determine the molecular weight of unknown gases by finding it from their rates of diffusion or effusion.
• It can be used to calculate the vapor density of a gas.
• The separation of isotopes of certain elements based on their molar mass has been made possible due to Graham's law of effusion. This method proved to be a breakthrough in creating the atomic bomb.

You might also be interested in calculating the ionic strength of solutions, which is why we have the perfect tool for you, the ionic strength calculator.