Radiocarbon Dating Calculator (Carbon 14 Dating)

Use Omni's radiocarbon dating calculator to determine the age of prehistoric organic (carbon-based) samples. This radiocarbon dating calculator uses the carbon 14 dating technique to determine the age of archaeological artifacts from the percentage of carbon-14 (¹⁴C) left in it.

If you don't know what carbon dating is or how to use our calculator, there's no need to worry! Read on to learn about the definition of carbon dating and the formula for carbon dating calculations. We have also explained in detail how does carbon dating work. You will also find some cool applications of the carbon dating technique and an example of how to use our calculator.

Have you ever wondered how archaeologists determined that the Maya civilization collapsed between the 8th and 9th centuries? Or that Tutankhamun, also known by his moniker King Tut, ruled during the end of the 18th Dynasty?

The answer is that they use a technique called radiocarbon dating (also known as carbon dating or carbon-14 dating) to reveal what happened in our past.

Carbon dating is a technique used to determine the age of organic materials or, to be more precise, the time elapsed since the death of the plant or animal the material came from. It relies on measuring the amount of radioactive carbon isotope ¹⁴C left in the sample and then correlating it with the half-life of carbon 14. The measurement corresponds to a reading of the activity of the isotope. We do have a half life calculator, if you are interested in wanting to know more about it.

The technique was developed in the 1940s by Prof. Willard F. Libby, who eventually won a Nobel Prize for this discovery.

The element carbon has three naturally occurring isotopes:

• Carbon-12 (¹²C);
• Carbon-13 (¹³C); and
• Carbon-14 (¹⁴C).

About 99% of the naturally occurring carbon on earth is carbon-12, and about 1% is carbon-13. Carbon-14 has an abundance of about 1 part per trillion of carbon-12.

The isotopes carbon-12 and carbon-13 are stable, but carbon-14 is radioactive. It decays into nitrogen-14 (¹⁴N) through beta decay. The half-life of carbon-14 is about 5,730 years, which means that after 5,730 years, half of the original amount of carbon-14 will have decayed into nitrogen-14.

Carbon-14 is continually being produced in the upper atmosphere where nitrogen-14 (¹⁴N) atoms are bombarded with neutrons produced by cosmic rays. The chemical properties of ¹⁴C are similar to those of ¹²C. Hence, once formed, it combines with oxygen and mixes into the biosphere just like ¹²C.

All plants and animals acquire a small amount of this radioactive ¹⁴C throughout their life, either through photosynthesis or through the food chain.

When a plant/animal dies, it stops absorbing new carbon-14 atoms. But the carbon-14 it has already assimilated continues decaying back to ¹⁴N with a half-life of 5,730 years. Hence, the carbon 14 content of dead tissues starts to decrease.

Thus, by measuring the amount of carbon 14 left in an object and comparing it with the expected normal amount present in living tissues, it is possible to determine the time elapsed or the age of any organic sample, as shown in the given figure.

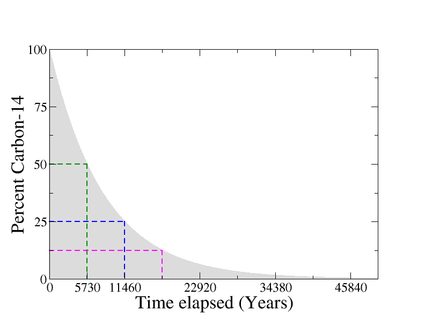
In other words, we use the carbon 14 decay as a "clock that starts counting when we die".

Let N_o be the amount of carbon-14 present in a living organism. According to the radioactive decay law, the number of carbon-14 atoms, $\text N$, left in a dead tissue sample after a certain time, $\text t$, is given by the exponential equation:

$\text N = \text N_\text o \text e^{-\lambda \text t}$

where $\lambda$ is the decay constant which is related to half-life $T_{1/2}$ by the equation:

$\lambda = \ln(2) / \text T_{1/2}$

Here, $\ln (2)$ is the natural logarithm of 2.

The percent of carbon-14 remaining after time $\text t$ is given by $\text N/\text N_\text o$. Using the first equation, we can determine $\lambda \text t$. The half-life of carbon-14 is 5,730 years; thus, we can calculate $\lambda$ using the second equation and then find $\text t$.

Some famous examples of the application of carbon-14 dating are:

1. Dating of the Shroud of Turin;
2. Uncovering modern art forgeries;
3. Radiocarbon dating of the mummies at the Louvre Museum;
4. Verification of the historical chronology of ancient Egypt; and
5. Solving the debate over world's oldest tattoos.

Might we interest you in our radioactive decay calculator to teach you how the activity of a substance is measured?

Let us determine the age of a wooden object found in an archaeological dig using our online radiocarbon dating calculator. Let the amount of carbon-14 found in the sample be 92 percent of that in a living tree:

1. Enter the percentage of carbon-14 left in the sample, i.e., 92 in the first row.
2. The half-life of carbon 14 is 5,730 years. This field is already prefilled.
3. You will get the calculated time elapsed, i.e., 689 years, in the third row, and the sample's age, i.e., 690 (+/-5) years, as the final result.
4. The sample's age is the time elapsed rounded off according to the standard convention mentioned in Stuiver and Polach, 1977.
5. If you want the age/time in other units, use our time unit converter calculator.

See how simple it is to use our online radiocarbon dating calculator!